In series combination of resistances :
p.d. is same across each resistance
total resistance is reduced
current is same in each resistance
all above are true.
The correct Answer is:C
To solve the question regarding the series combination of resistances, let's analyze the statements one by one.
1. Understanding Series Combination:
In a series combination, resistors are connected end-to-end, and the same current flows through each resistor. Let's denote the resistors as R1 and R2.
2. Total Resistance in Series:
The total or equivalent resistance Rnet in a series circuit is calculated by simply adding the individual resistances:
Rnet=R1+R2
This means the total resistance is greater than any individual resistance.
3. Potential Difference Across Each Resistor:
According to Ohm's Law, the potential difference V across a resistor is given by:
V=I⋅R
In a series circuit, the total voltage V from the battery is divided among the resistors. The voltage across R1 is:
VR1=I⋅R1
And the voltage across R2 is:
VR2=I⋅R2
Since R1 and R2 are not necessarily equal, the potential difference across each resistor is not the same. Therefore, the first statement is false.
4. Current in the Circuit:
In a series circuit, the same current I flows through each resistor. The current can be calculated using the total voltage and total resistance:
I=VRnet=VR1+R2
Since the same current flows through both R1 and R2, the third statement is true.
5. Conclusion on Total Resistance:
The total resistance in a series combination is not reduced; it is increased. Therefore, the second statement is false.
Summary of Results:
- First Statement: False (Potential difference is not the same across each resistance)
- Second Statement: False (Total resistance is increased)
- Third Statement: True (Current is the same in each resistor)
Final Answer:
The only true statement regarding the series combination of resistances is that the current is the same in each resistor.
---
In a series combination, resistors are connected end-to-end, and the same current flows through each resistor. Let's denote the resistors as R1 and R2.
The total or equivalent resistance Rnet in a series circuit is calculated by simply adding the individual resistances:
Rnet=R1+R2
This means the total resistance is greater than any individual resistance.
According to Ohm's Law, the potential difference V across a resistor is given by:
V=I⋅R
In a series circuit, the total voltage V from the battery is divided among the resistors. The voltage across R1 is:
VR1=I⋅R1
And the voltage across R2 is:
VR2=I⋅R2
Since R1 and R2 are not necessarily equal, the potential difference across each resistor is not the same. Therefore, the first statement is false.
In a series circuit, the same current I flows through each resistor. The current can be calculated using the total voltage and total resistance:
I=VRnet=VR1+R2
Since the same current flows through both R1 and R2, the third statement is true.
The total resistance in a series combination is not reduced; it is increased. Therefore, the second statement is false.
- First Statement: False (Potential difference is not the same across each resistance)
- Second Statement: False (Total resistance is increased)
- Third Statement: True (Current is the same in each resistor)
The only true statement regarding the series combination of resistances is that the current is the same in each resistor.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (NUMERICALS )
54 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B)
15 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Video
Similar Questions
A sinusoidal voltage Vsin(at) is applied across a series combination of resistance R and inductor L. The amplitude of the current in the circuit is
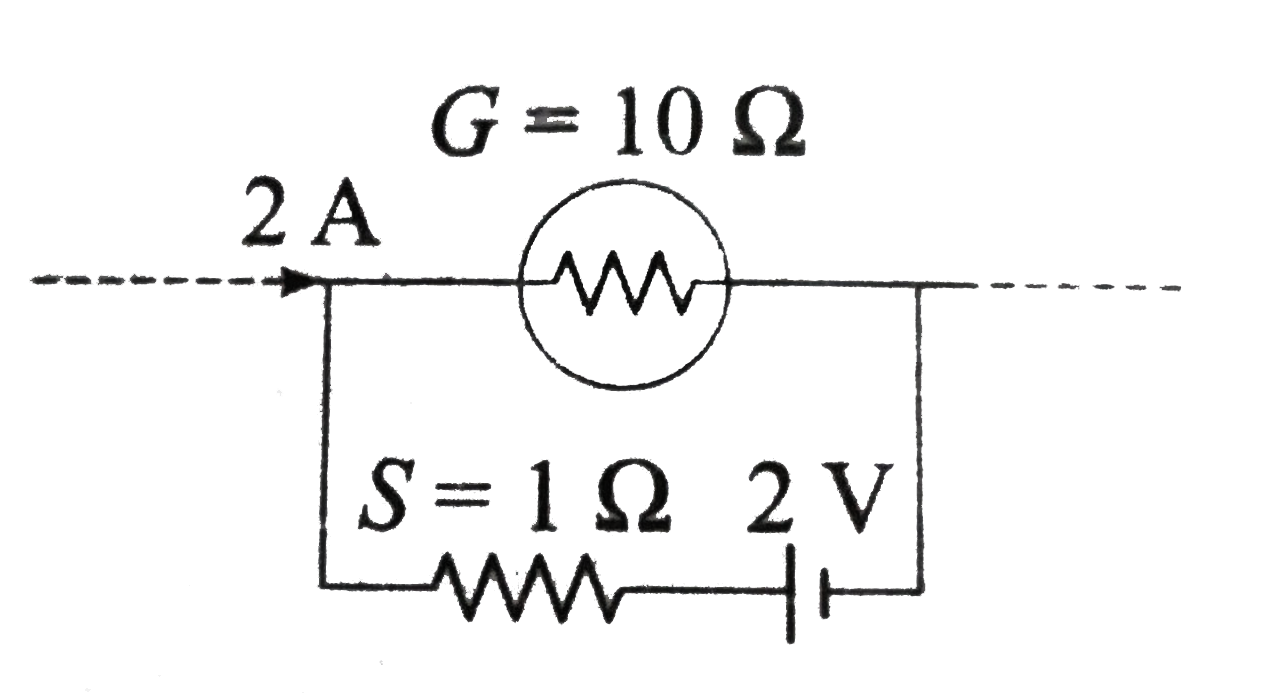
View SolutionThe galvanometer shown in the figure has resistance 10Ω. It is shunted by a series combination of a resistance S=1Ω and an ideal cell of emf 2 V. A current 2 A passes as shown.

View Solution
Knowledge Check
In parallel combination of resistances :
Ap.d. is same across each resistanceBtotal resistance is increasedCcurrent is same in each resistanceDall above are true.The correct combination of three resistances 1Ω,2Ωand3Ω to get equivalent resistance 115Ω is
AAll three are combines in paralleBAll three are combines in paralleC1Ωand2Ω in parallel and 3Ω is in series to bothD2Ωand3Ω in parallel and 3Ω is in series to bothIn the series combination of n cells each cell having emf ε and internal resistance r. If three cells are wrongly connected, then total emf and internal resistance of this combination will be
Anε,(nr−3r)B(nε−2r),nrC(nε−4ε),nrD(nε−6ε),nr
The resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionThe following combination are concerned with experiments of the characterization and use of a moving coil galvanometer.
The series combination of variab resistance R, one 100Ω resistor and moving coil galvanometer is connected to a mobile phone charger having negligible internal resistance. The zero of the galvanometer lies the centre and the pointer can move 30 division full scale on either side depending on the directin of current. The reading of the galvanometer is 10 divisions and the voltages across the galvanometer and 100Ω resistor are respectively 12mV and 16 mV.
The series combination of the galvanometer with a resistnce of R is conneted across an ideal voltage supply of 12 V and this time the galvanometer shows full scale defiention of 30 divisions.
The value of R is nearly
View SolutionA carbon and an aluminium wire are connected in series. If the combination has resistance of 30Ω at 30∘C, what is the resistance of each wire at 0∘Cso that resistance of the combination does not change with temperature.(ac=−0.5×10−3/∘C,aA=4×10−3/∘C)
View Solution