In parallel combination of resistances :
p.d. is same across each resistance
total resistance is increased
current is same in each resistance
all above are true.
The correct Answer is:A
To solve the question regarding the characteristics of resistances in a parallel combination, we will analyze each statement provided in the options step by step.
Step 1: Understanding Parallel Combination of Resistors
In a parallel combination, two or more resistors are connected across the same two points. This means that the voltage (potential difference) across each resistor is the same.
Hint: Remember that in parallel circuits, the voltage across each component is equal to the voltage of the source.
Step 2: Analyzing the First Statement
The first statement claims that the potential difference is the same across each resistance. Since resistors R1 and R2 are connected in parallel, the voltage across R1 (V_R1) and the voltage across R2 (V_R2) is equal to the voltage of the battery (V).
- Conclusion: This statement is true.
Hint: Use the concept of Kirchhoff's Voltage Law (KVL) to understand how voltage behaves in parallel circuits.
Step 3: Analyzing the Second Statement
The second statement claims that the total resistance is increased in a parallel combination. To find the total (or equivalent) resistance (R_net) in a parallel circuit, we use the formula:
1Rnet=1R1+1R2
This means that:
Rnet=R1⋅R2R1+R2
From this formula, we can see that R_net is always less than either R1 or R2 (assuming R1 and R2 are positive values).
- Conclusion: This statement is false; the total resistance decreases in a parallel combination.
Hint: Remember that combining resistors in parallel decreases the overall resistance, making it easier for current to flow.
Step 4: Analyzing the Third Statement
The third statement claims that the current is the same in each resistance. The current through each resistor can be calculated using Ohm's law:
I1=VR1andI2=VR2
Since R1 and R2 can be different, the currents I1 and I2 will also be different.
- Conclusion: This statement is false; the current is not the same in each resistance.
Hint: Recall that in parallel circuits, while voltage is constant, the current can vary depending on the resistance values.
Step 5: Analyzing the Fourth Statement
The fourth statement claims that all the above statements are true. Since we have determined that the second and third statements are false, this statement must also be false.
- Conclusion: This statement is false.
Hint: If any of the individual statements are false, then the conclusion that all are true must also be false.
Final Conclusion
Based on the analysis:
- The first statement is true.
- The second and third statements are false.
- The fourth statement is false.
Thus, the correct option is A: Potential difference is the same across each resistance.
In a parallel combination, two or more resistors are connected across the same two points. This means that the voltage (potential difference) across each resistor is the same.
The first statement claims that the potential difference is the same across each resistance. Since resistors R1 and R2 are connected in parallel, the voltage across R1 (V_R1) and the voltage across R2 (V_R2) is equal to the voltage of the battery (V).
The second statement claims that the total resistance is increased in a parallel combination. To find the total (or equivalent) resistance (R_net) in a parallel circuit, we use the formula:
The third statement claims that the current is the same in each resistance. The current through each resistor can be calculated using Ohm's law:
The fourth statement claims that all the above statements are true. Since we have determined that the second and third statements are false, this statement must also be false.
Based on the analysis:
- The first statement is true.
- The second and third statements are false.
- The fourth statement is false.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (NUMERICALS )
54 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B)
15 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
A 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View Solution
Assertion: In the circuit shown in figure after closing the switch S reading of ammeter will increase while that of voltmeter will decrease.
Reason : Net resistance decreases as parallel combination of resistors is increased,
View Solution
Knowledge Check
In series combination of resistances :
Ap.d. is same across each resistanceBtotal resistance is reducedCcurrent is same in each resistanceDall above are true.The total resistance in the parallel combination of three resistances 9Ω,7Ωand5Ω
A1.22ΩB2.29ΩC4.22ΩD2.02ΩIn parallel combination of n cells, we obtain
Amore voltageBmore currentCless voltageDless current
The V-I graph for a series combination and for a parallel combination of two resistor is shown in the figure below. Which of the two A or B, represents the parallel combination? Give a reason for your answer.
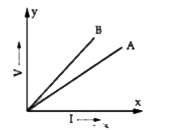
View SolutionThe V-I graph for a series combination and for a parallel combination of two resistors is 1 shown in Fig. Which of the V two, A or B, represents the parallel combination ? Give a reason for your answer.
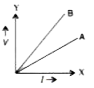
View SolutionThe V-I graph for a series combination and for a parallel combination of two resistor is shown in the figure below. Which of the two A or B, represents the parallel combination? Give a reason for your answer.
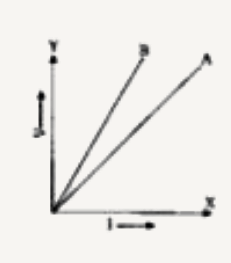
View SolutionThe series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
View SolutionThe series combination of two batteries, both of the same emf 20 V, but different internal resistance of 10 Ω and 2 Ω , is connected to the parallel combination of two resistors 10 ohm and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R(∈Ω) is _________.
View Solution
