For a ray of light refracted through a prism of angle , the angle of incidence is equal to the angle of emergence, each equal to . Find the refractive index of the material of the prism.
To find the refractive index of the material of a prism with an angle of 60 degrees, where the angle of incidence (I) and angle of emergence (E) are both 45 degrees, we can follow these steps:
1. Identify the Given Values:
- Angle of the prism (A) = 60 degrees
- Angle of incidence (I) = 45 degrees
- Angle of emergence (E) = 45 degrees
2. Recognize the Condition of Minimum Deviation:
- Since the angle of incidence is equal to the angle of emergence (I = E), we are dealing with the case of minimum deviation. In this case, the angles of refraction at both faces of the prism are equal (r1 = r2 = r).
3. Relate the Angles:
- For a prism, the relationship between the angle of the prism (A), angle of refraction (r), and the angles of incidence and emergence can be expressed as:
A=r1+r2
- Since r1=r2=r, we can write:
A=2r
- Therefore, we can find r:
r=A2=60∘2=30∘
4. Use Snell's Law:
- Snell's Law states that:
n=sinIsinr
- Here, n is the refractive index, I is the angle of incidence, and r is the angle of refraction.
5. Calculate the Sine Values:
- Calculate sinI and sinr:
- sinI=sin45∘=1√2
- sinr=sin30∘=12
6. Substitute into Snell's Law:
- Substitute the values into the formula for the refractive index:
n=sinIsinr=1√212=1√2×2=2√2=√2
7. Final Answer:
- The refractive index of the material of the prism is:
n=√2
- Angle of the prism (A) = 60 degrees
- Angle of incidence (I) = 45 degrees
- Angle of emergence (E) = 45 degrees
- Since the angle of incidence is equal to the angle of emergence (I = E), we are dealing with the case of minimum deviation. In this case, the angles of refraction at both faces of the prism are equal (r1 = r2 = r).
- For a prism, the relationship between the angle of the prism (A), angle of refraction (r), and the angles of incidence and emergence can be expressed as:
A=r1+r2
- Since r1=r2=r, we can write:
A=2r
- Therefore, we can find r:
r=A2=60∘2=30∘
- Snell's Law states that:
n=sinIsinr
- Here, n is the refractive index, I is the angle of incidence, and r is the angle of refraction.
- Calculate sinI and sinr:
- sinI=sin45∘=1√2
- sinr=sin30∘=12
- Substitute the values into the formula for the refractive index:
n=sinIsinr=1√212=1√2×2=2√2=√2
- The refractive index of the material of the prism is:
n=√2
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTE ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:EXERCISE
Explore 45 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTE ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSIGNMENT (SECTION - A)
Explore 39 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTE ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 7 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Book:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Exercise:Assignment SECTION - D (Assertion & reason type Question)
Explore 10 Videos
Similar Questions
The angle of minimum deviation from a prism is 37∘. If the angle of prism is 53∘, find the refractive index of the material of the prism.
View SolutionA ray of light passes through an equilateral glass prism in such a manner that the angle of incidence is equal to the angle of emergence and each of these angles is equal to 3/4 of the angle of the prism. The angle of deviation is
View Solution
Knowledge Check
A ray of light passes through an equilateral prism (refractive index 1.5) such that angle of incidence is equal to angle of emergence and the latter is equal to 3/4th of the angle of prism. Calculate the angle of deviation.
A60∘B30∘C45∘D120∘
In an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
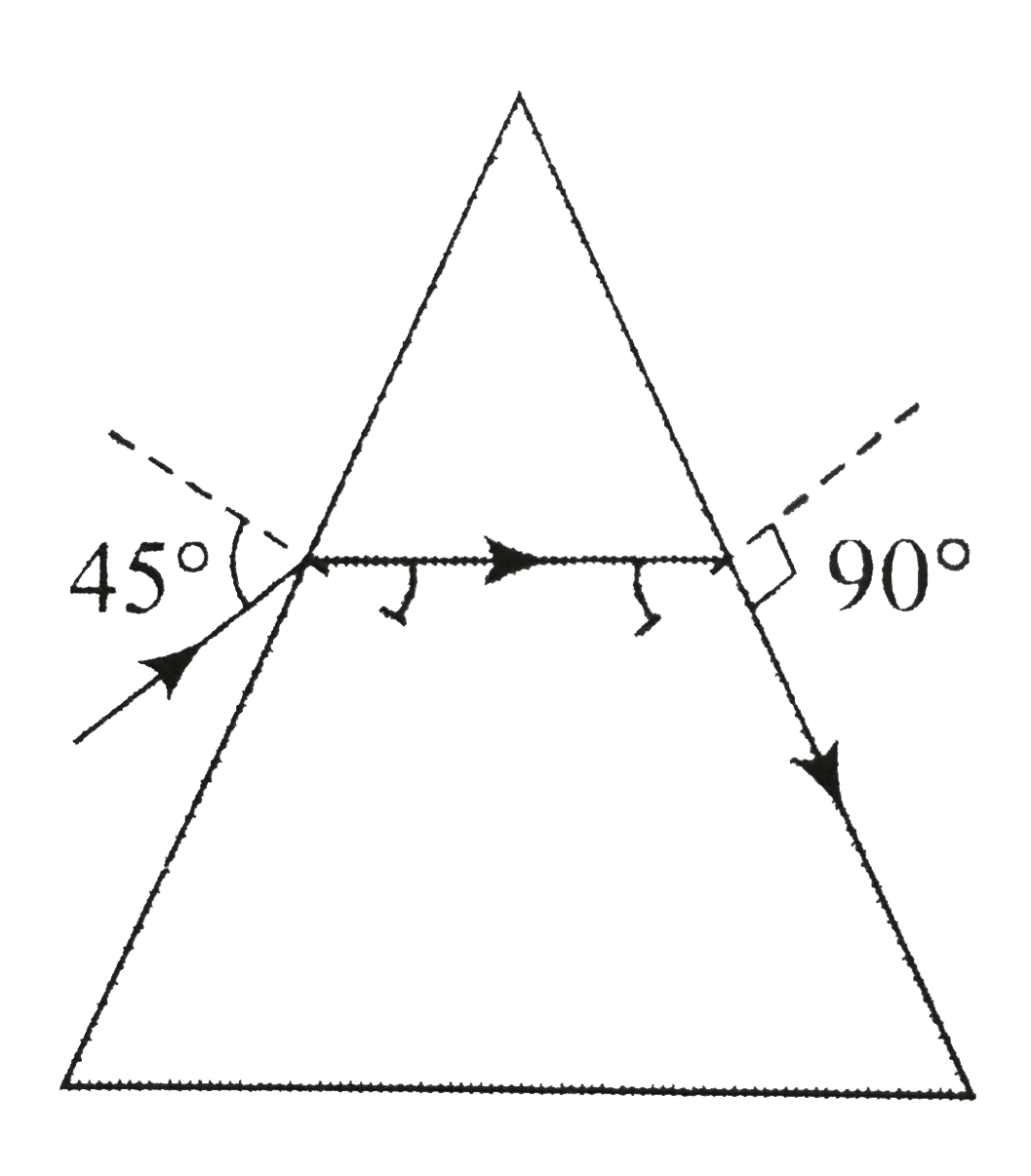
View SolutionA ray of light passes through the equilateral prism such that angle of incidence is equal to the angle of emergence if the angle of incidence is 45∘. The angle of deviation will be
View SolutionA ray of light falling at an angle of 50∘ is refracted through a prism and suffers minimum deviation. The angle of the prism is 60∘. Find the angle of minimum deviation and refraction index of the material of the prism.
View SolutionOne of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionIf the angle of minimum deviation is of 60∘ for an equilateral prism , then the refractive index of the material of the prism is
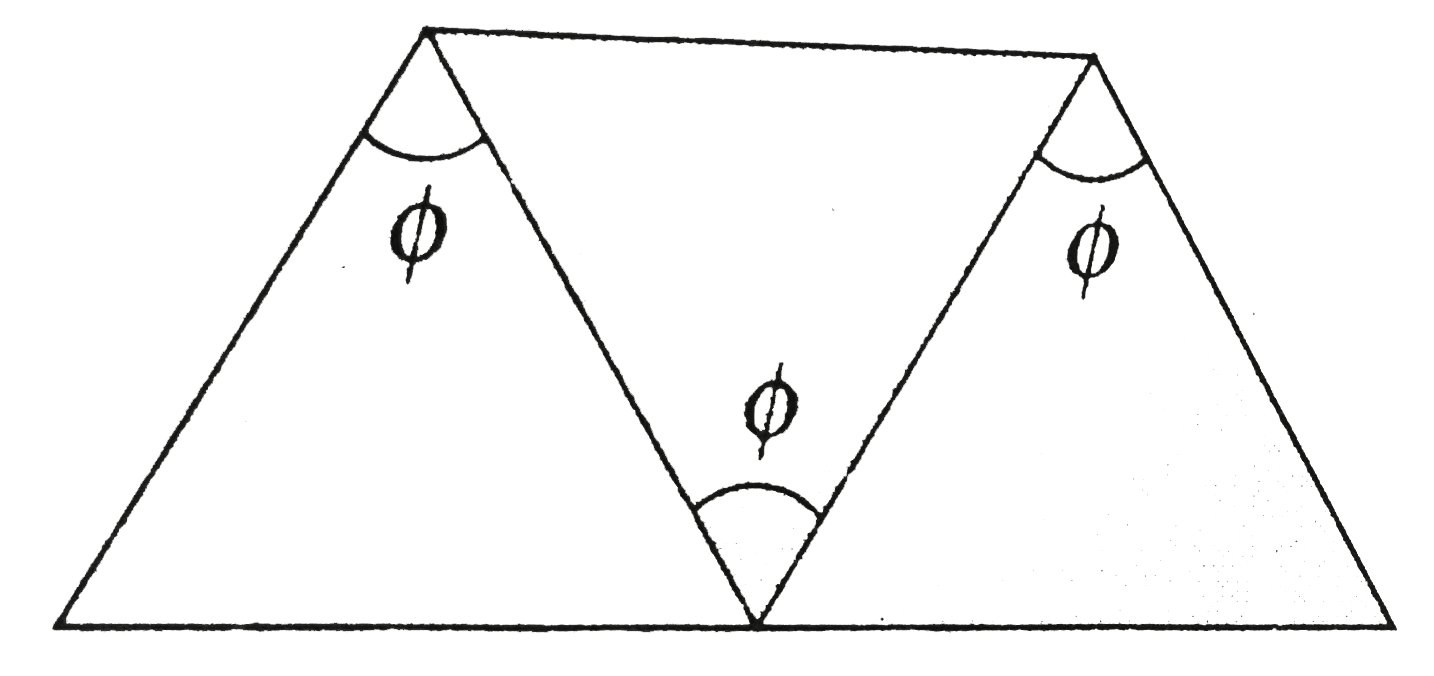
View SolutionA direct-vision prism is made out of three prisms, each with a refracting angle of ϕ=60∘ , attached to each other as shown in Figure. Light of a certain wavelength is incident on the first prism. The angle of incidence is 30∘ and the ray leaves the third prism parallel to the direction of incidence. The refractive index of the glass of the first and third prisms, is 1.5. Find the refractive index of the material of the middle prism. (√6=2.45)
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes thorugh the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
View Solution
