Show that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
To show that for refraction at a concave spherical surface (separating glass and air), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real, we can follow these steps:
1. Identify the Refractive Indices:
- Let the refractive index of glass (medium 1) be μ1=1.5.
- Let the refractive index of air (medium 2) be μ2=1.0.
2. Sign Convention:
- Since we are dealing with a concave surface, we will take the radius of curvature R to be negative (i.e., R<0).
- The object distance u will also be negative (i.e., u<0) as per the sign convention for the Cartesian coordinate system.
3. Use the Refraction Formula:
- The formula for refraction at a spherical surface is given by:
μ2V−μ1U=μ2−μ1R
- Substituting the values:
1.0V−1.5−u=1.0−1.5−R
- This simplifies to:
1V+1.5u=0.5−R
4. Rearranging the Equation:
- Rearranging gives:
1V=−0.5R−1.5u
- This can be rewritten as:
1V=12R−32u
5. Condition for Real Image:
- For the image to be real, V must be positive. Therefore:
12R−32u>0
- This implies:
12R>32u
- Rearranging gives:
u>3R
6. Conclusion:
- Thus, we have shown that for the image to be real, the object distance u must be greater than three times the radius of curvature R:
u>3R
- Let the refractive index of glass (medium 1) be μ1=1.5.
- Let the refractive index of air (medium 2) be μ2=1.0.
- Since we are dealing with a concave surface, we will take the radius of curvature R to be negative (i.e., R<0).
- The object distance u will also be negative (i.e., u<0) as per the sign convention for the Cartesian coordinate system.
- The formula for refraction at a spherical surface is given by:
μ2V−μ1U=μ2−μ1R
- Substituting the values:
1.0V−1.5−u=1.0−1.5−R
- This simplifies to:
1V+1.5u=0.5−R
- Rearranging gives:
1V=−0.5R−1.5u
- This can be rewritten as:
1V=12R−32u
- For the image to be real, V must be positive. Therefore:
12R−32u>0
- This implies:
12R>32u
- Rearranging gives:
u>3R
- Thus, we have shown that for the image to be real, the object distance u must be greater than three times the radius of curvature R:
u>3R
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - A)
39 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - J) Aakash Challengers Questions
7 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
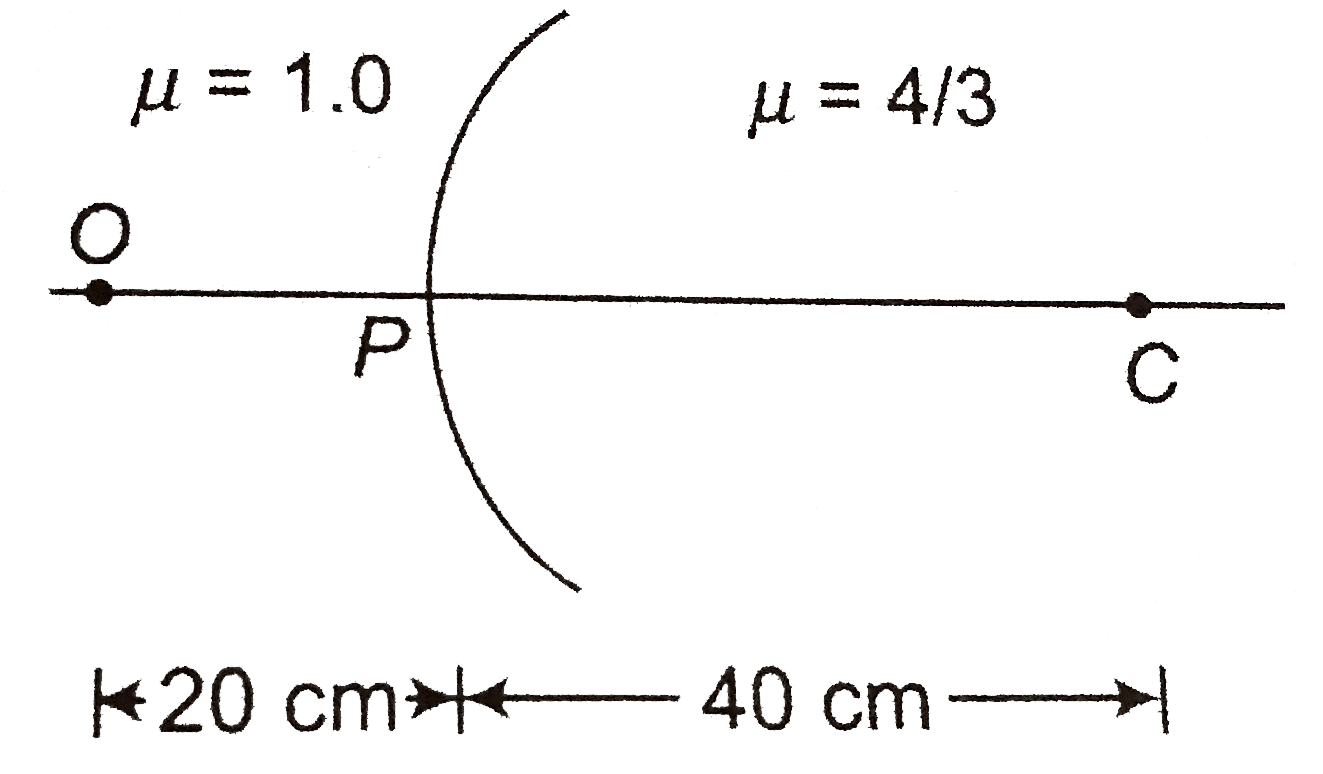
Locate the image of the point object O. The point C is centre of curvature of the spherical surface.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionThe minimum sum of the distances of a real object and a real image from a concave mirror of radius of curvature 20cm is:
View SolutionRefraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance (μg=3/2)
Note Object lying in the glass.
View SolutionRadius of curvature of a concave spherical surface separating air-glass medium is R. A point object is placed on the principal axis in the glass (mg=1.5). For the image to be real seen by

observer in air, distance of the object from P should be
View SolutionTrace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
View SolutionA convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:

View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View Solution
