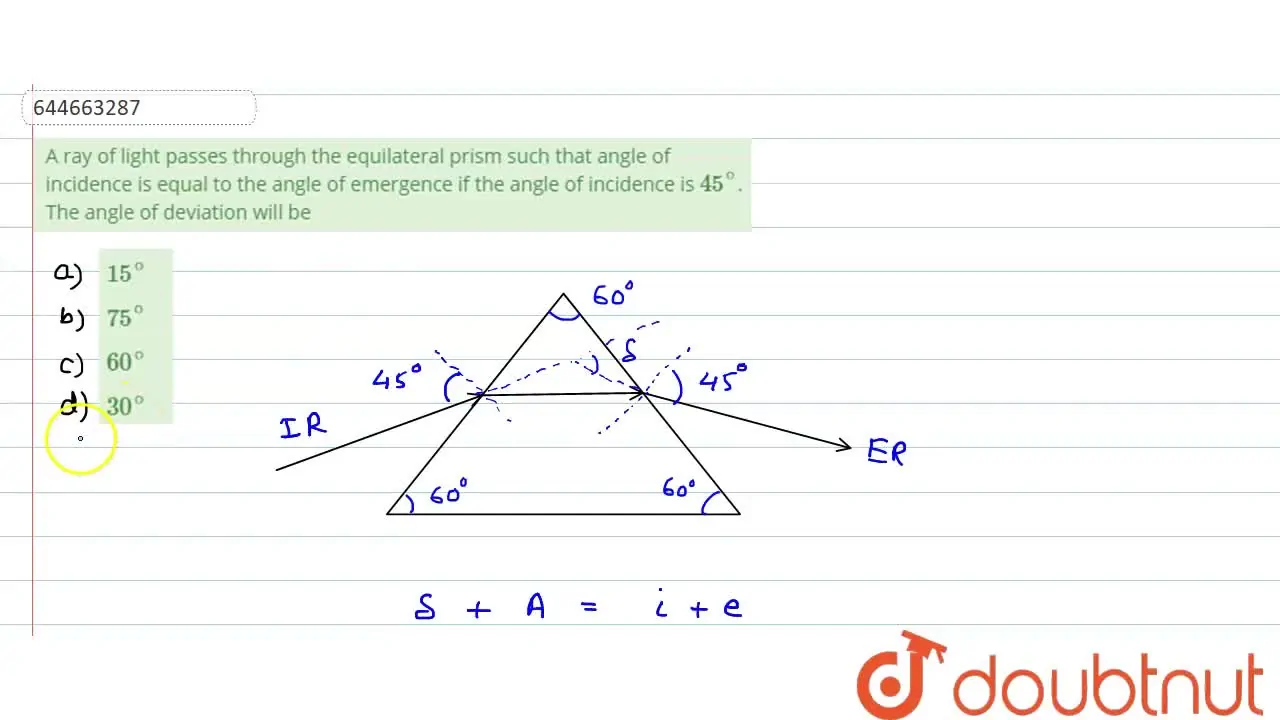
A ray of light passes through the equilateral prism such that angle of incidence is equal to the angle of emergence if the angle of incidence is 45∘. The angle of deviation will be
15∘
75∘
60∘
30∘
The correct Answer is:4
Step by step video & image solution for A ray of light passes through the equilateral prism such that angle of incidence is equal to the angle of emergence if the angle of incidence is 45^(@). The angle of deviation will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-114videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-122videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-97videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS30videos
QUIZ
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE58videos
RAY OPTICS AND WAVE OPTICS
Similar Questions
A ray of light passes through an equilateral glass prism in such a manner that the angle of incidence is equal to the angle of emergence and each of these angles is equal to 3/4 of the angle of the prism. The angle of deviation is
View SolutionA ray of light passes through an equilateral prism (refractive index 1.5) such that angle of incidence is equal to angle of emergence and the latter is equal to 3/4th of the angle of prism. Calculate the angle of deviation.
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View SolutionDraw a neat diagram for the passage of a ray of light through an equilateral glass prism, showing clearly
(a) angle of incidence (b) angle of emergence ( c ) angle of deviation (d) angle of prismView SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View Solution(a) Define the following when refraction takes place through an equilateral glass prism
(i) angle of incidence (ii) prism (iii) refracting angle of prism (iv) angle of emergence (v) angle of deviation
(b) How are angle of incidence, angle of prism, angle of emergence and angle of deviation related to each other?View SolutionWrite a relation for the angle of deviation (δ) for a ray of light passing through an equilateral prism in terms of the angle of incidence (i1), angle of emergence (i2) ang angle of prism (A).
View SolutionA ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2.
(i) How is the angle of emergence 'i1' related to the angle of incidence 'i1' ?
(Ii) What can you say about the angle of deviation in such a situation ?View SolutionA ray of light passing through a prism having refractive index √2 suffers minimum deviation. It is found that the angle of incidence is double the angle of refraction within the prism. What is the angle of prism?
View SolutionAn equilateral prism deviates a ray through 45∘ for the two angles of incidence differing by 20∘. The angle of incidence is
View Solution