The position of the top corner of the lecture room was required. To find this a theodolite was
set up as in the figure below. The distance to the side wall, along the x-axis is 7 m, and following
angles were measured AOX=60∘,AOY=45∘ Calculate the coordinates of the corner realtive
to the position of theodolite.
To find the coordinates of the top corner of the lecture room relative to the position of the theodolite, we can follow these steps:
Step 1: Understand the Given Information
- The distance to the side wall along the x-axis (OX) is given as 7 m.
- The angles measured are:
- ∠AOX=60∘
- ∠AOY=45∘
Step 2: Calculate the Distance OA
We can use the cosine of the angle ∠AOX to find the distance OA (the hypotenuse in the triangle formed by the x-axis and the line to point A).
Using the cosine formula:
cos(60∘)=OXOA
Substituting the known values:
cos(60∘)=7OA
Since cos(60∘)=12:
12=7OA
Cross-multiplying gives:
OA=14 m
Step 3: Calculate the Y-coordinate
Now, we will calculate the Y-coordinate using the angle ∠AOY.
Using the cosine formula again:
cos(45∘)=OYOA
Substituting the known values:
cos(45∘)=Y14
Since cos(45∘)=1√2:
1√2=Y14
Cross-multiplying gives:
Y=14√2=7√2 m
Step 4: Calculate the Z-coordinate
Next, we need to find the Z-coordinate using the angle ∠AOZ. To find this angle, we can use the relationship between the direction cosines.
Using the formula:
cos2(AOX)+cos2(AOY)+cos2(AOZ)=1
Substituting the known values:
cos2(60∘)+cos2(45∘)+cos2(AOZ)=1
Calculating the cosines:
(12)2+(1√2)2+cos2(AOZ)=1
This simplifies to:
14+12+cos2(AOZ)=1
Finding a common denominator (4):
14+24+cos2(AOZ)=1
34+cos2(AOZ)=1
cos2(AOZ)=1−34=14
Thus:
cos(AOZ)=12
This means:
AOZ=60∘
Now we can find the Z-coordinate:
Using the cosine formula:
cos(60∘)=ZOA
Substituting the known values:
12=Z14
Cross-multiplying gives:
Z=7 m
Step 5: Final Coordinates
Now we have all the coordinates:
- X=7
- Y=7√2
- Z=7
Thus, the coordinates of the top corner of the lecture room relative to the position of the theodolite are:
(7,7√2,7)
- The distance to the side wall along the x-axis (OX) is given as 7 m.
- The angles measured are:
- ∠AOX=60∘
- ∠AOY=45∘
We can use the cosine of the angle ∠AOX to find the distance OA (the hypotenuse in the triangle formed by the x-axis and the line to point A).
cos(60∘)=OXOA
Substituting the known values:
cos(60∘)=7OA
Since cos(60∘)=12:
12=7OA
Cross-multiplying gives:
OA=14 m
Now, we will calculate the Y-coordinate using the angle ∠AOY.
cos(45∘)=OYOA
Substituting the known values:
cos(45∘)=Y14
Since cos(45∘)=1√2:
1√2=Y14
Cross-multiplying gives:
Y=14√2=7√2 m
Next, we need to find the Z-coordinate using the angle ∠AOZ. To find this angle, we can use the relationship between the direction cosines.
cos2(AOX)+cos2(AOY)+cos2(AOZ)=1
Substituting the known values:
cos2(60∘)+cos2(45∘)+cos2(AOZ)=1
Calculating the cosines:
(12)2+(1√2)2+cos2(AOZ)=1
This simplifies to:
14+12+cos2(AOZ)=1
Finding a common denominator (4):
14+24+cos2(AOZ)=1
34+cos2(AOZ)=1
cos2(AOZ)=1−34=14
Thus:
cos(AOZ)=12
This means:
AOZ=60∘
Using the cosine formula:
cos(60∘)=ZOA
Substituting the known values:
12=Z14
Cross-multiplying gives:
Z=7 m
Now we have all the coordinates:
- X=7
- Y=7√2
- Z=7
(7,7√2,7)
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration
4 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
A coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or 30∘ with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
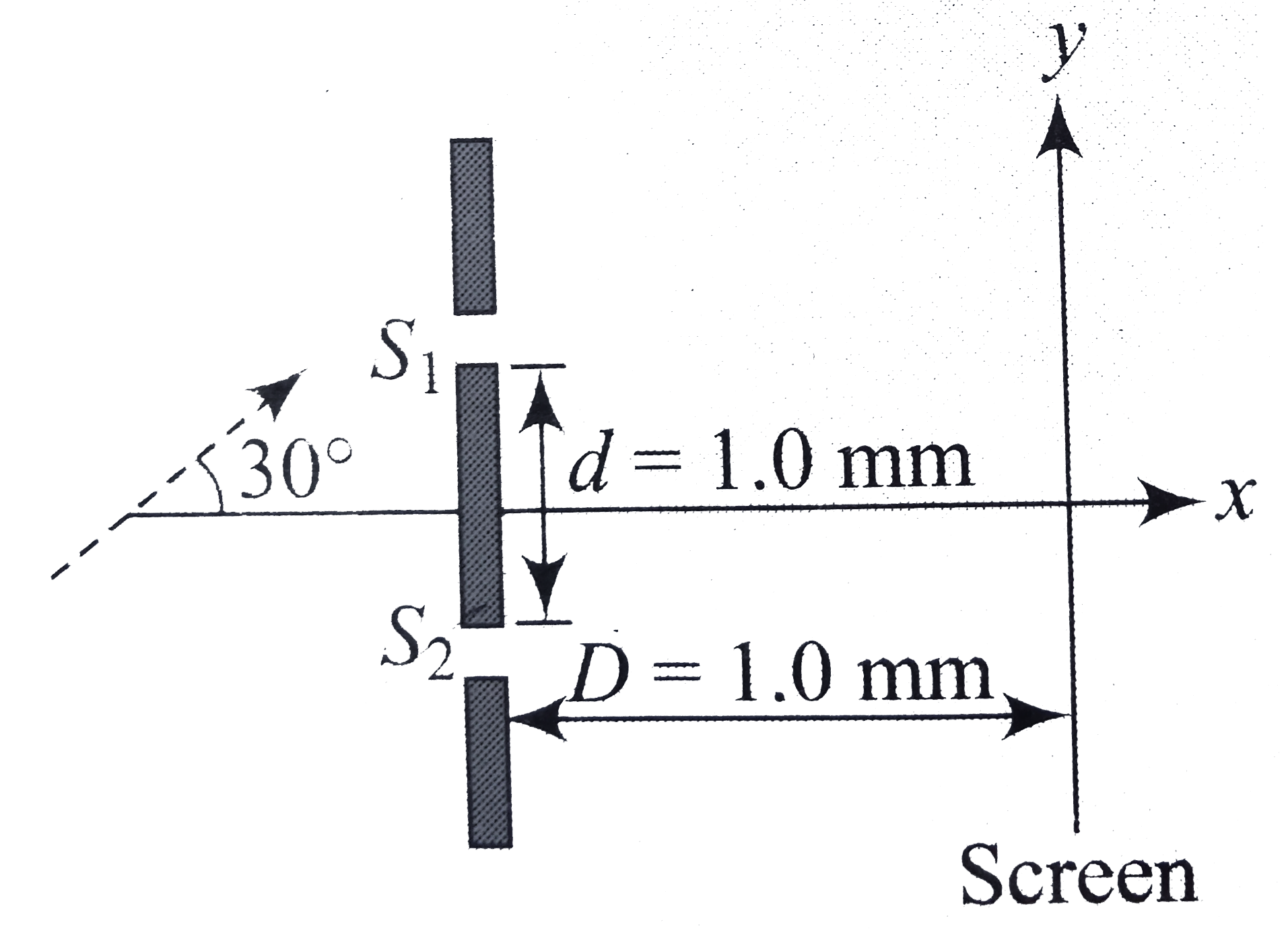
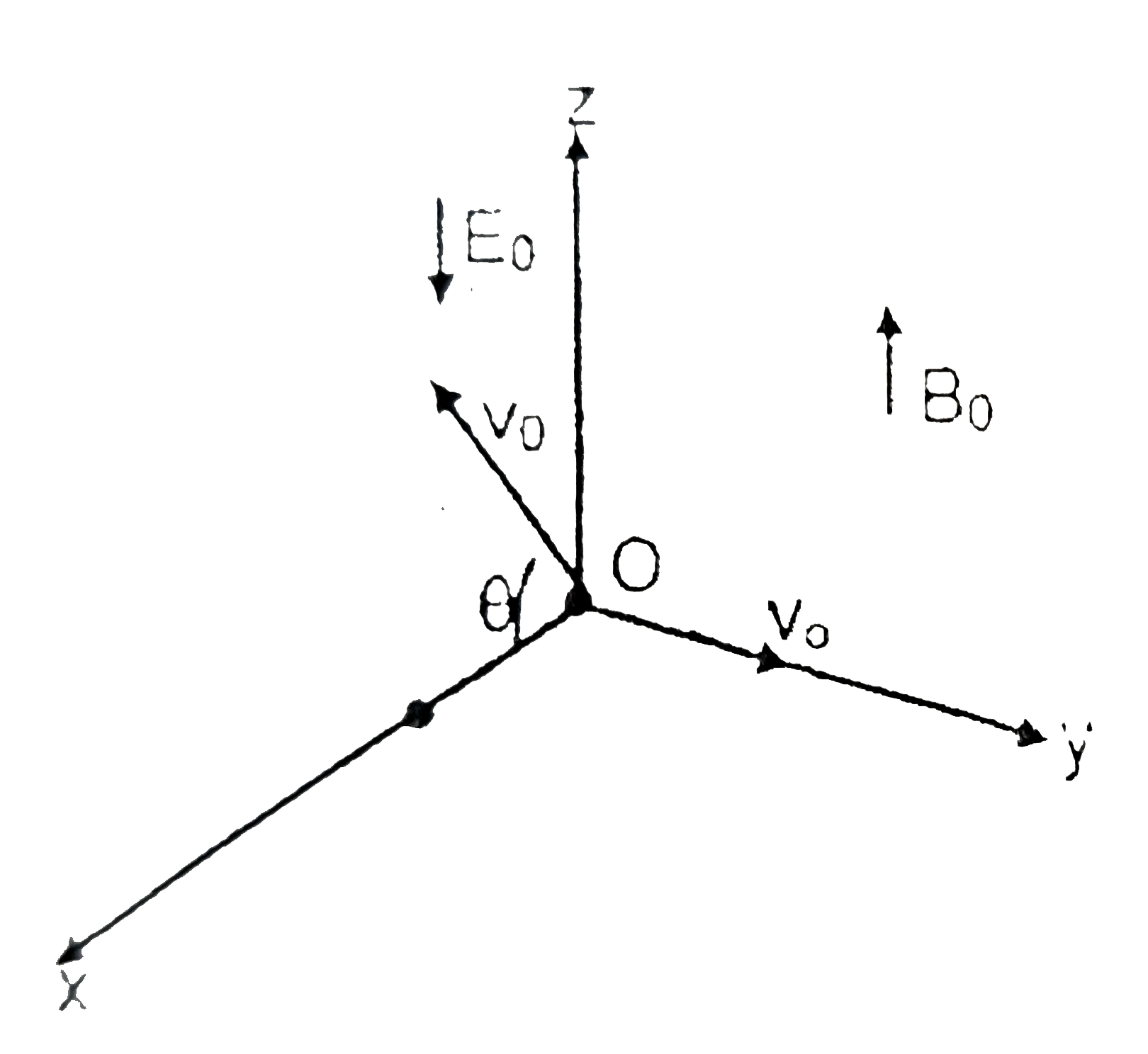
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
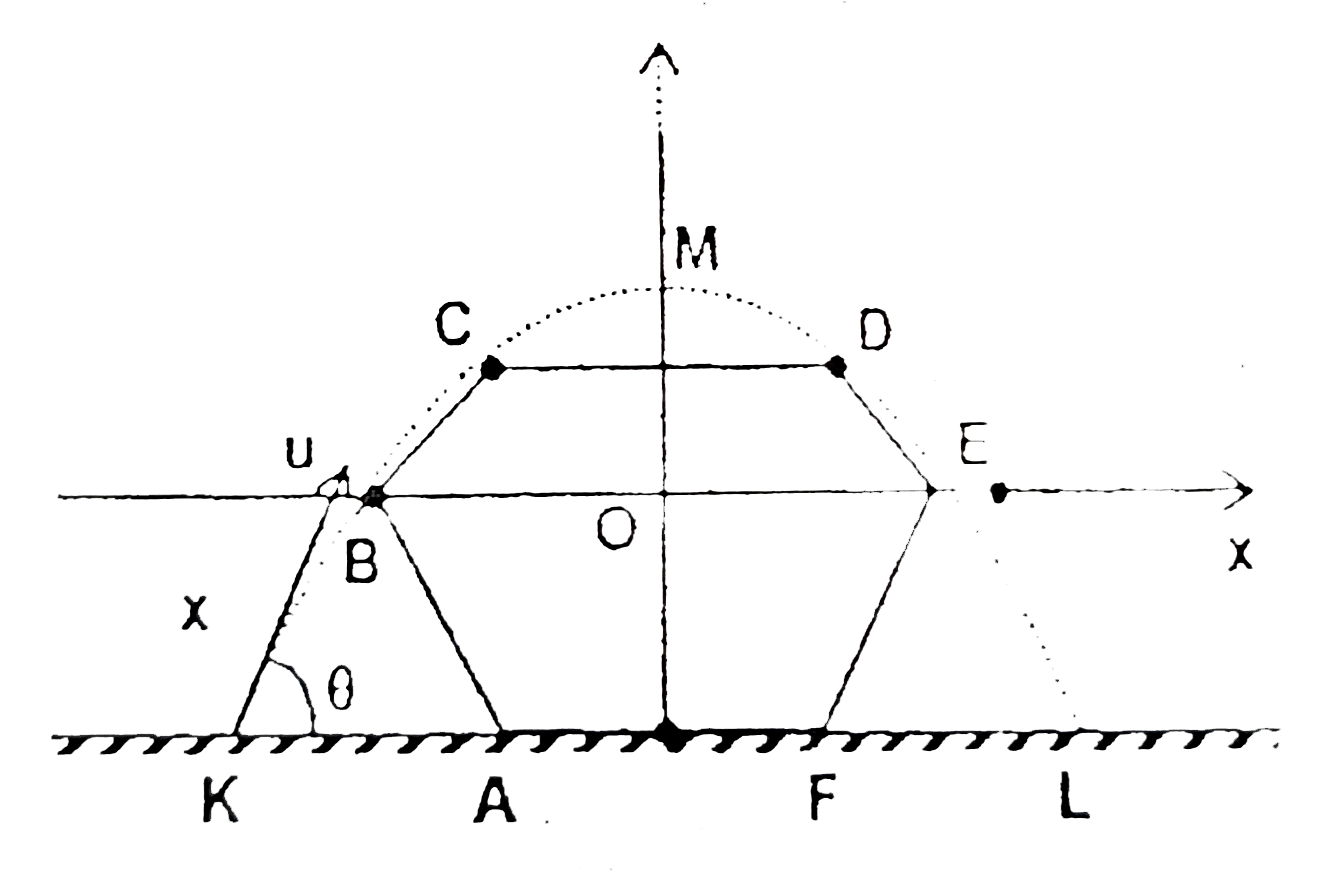
View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The time required to move the particle from D to E is
View SolutionA thin equiconvex lens made of glass of refractive index 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (μ=32). On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance oa 0.9m from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

View SolutionAn electron gun G emits electons of energy 2keV travelling in the positive x-direction. The electons are required to hit the spot S where GS=0.1m, and the line GS makes an angle of 60∘ with the x-axis as shown in figure. A uniform magnetic field B parallel to GS exists in the region outside the electron gun.

find the minimum value of B needed to make the electrons hit S.
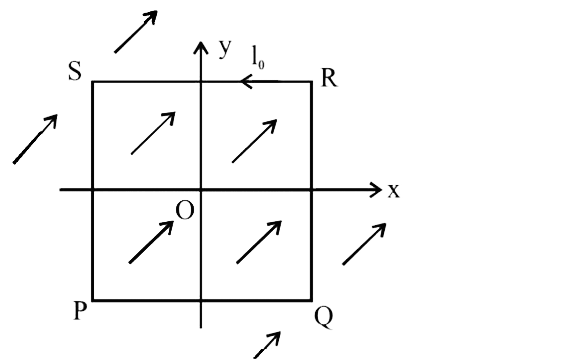
View SolutionA uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).
View SolutionFour particles, each of mass 1kg, are placed at the corners of a square OABC of side 1m. 'O' is at the origin of the coordinate system. OA and OC are aligned along positive x-axis and positive y-axis respectively. The position vector of the centre of mass is (in 'm')
View SolutionA uniform magnetic field →B is set up along the positive x-axis. A particle of charge 'q' and mass 'm' moving with a velocity →v entresthe field at the origin in X-Y plane such that it has velocity companents both along and perpendicular to the magnetic field →B. Trace, giving reason. the fraectory followed by the particle . Find out the expression for the distance moved by the particle along the magnetic field in one rotation.
View SolutionWater is filled to a height of 2.5m in a container lying rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side √3 and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than 4×104 pascal
a, What minimum acceleration can be given to the container in the positive x-direction so that the cap will come out of the hole? Assume water does not spill out of container when the container accelerates.
Find the velocity of efflux as soon as the container starts moving with the acceleration calculated in part a. of the question.

View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View Solution
