A uniform magnetic field →B is set up along the positive x-axis. A particle of charge 'q' and mass 'm' moving with a velocity →v entresthe field at the origin in X-Y plane such that it has velocity companents both along and perpendicular to the magnetic field →B. Trace, giving reason. the fraectory followed by the particle . Find out the expression for the distance moved by the particle along the magnetic field in one rotation.
To solve the problem, we need to analyze the motion of a charged particle entering a uniform magnetic field. The magnetic field is directed along the positive x-axis, and the particle has both parallel and perpendicular components of velocity relative to the magnetic field.
1. Understanding the Motion:
- The magnetic field →B is directed along the x-axis.
- The particle has a charge q and mass m, and it enters the magnetic field with a velocity →v at the origin in the x-y plane.
- The velocity can be resolved into two components:
- vx=vcosθ (component along the x-axis, parallel to →B)
- vy=vsinθ (component along the y-axis, perpendicular to →B)
2. Path of the Particle:
- The component of the velocity vy will cause the particle to move in a circular motion due to the magnetic force acting on it.
- The component vx will cause the particle to move linearly along the x-axis.
- The combination of these two motions results in a helical trajectory.
3. Radius of the Helix:
- The radius r of the circular motion can be determined using the centripetal force provided by the magnetic force:
F=qvyB=mv2yr
- Rearranging gives:
r=mvyqB
- Substituting vy=vsinθ:
r=m(vsinθ)qB
4. Time Period of Rotation:
- The time period T for one complete rotation in the magnetic field can be derived from the circular motion:
T=2πrvy
- Substituting the expression for r:
T=2π(m(vsinθ)qB)vsinθ=2πmqB
5. Distance Moved Along the Magnetic Field in One Rotation:
- The distance moved along the x-axis (the pitch of the helix) during one complete rotation is given by:
Pitch=vx⋅T
- Substituting vx=vcosθ and T=2πmqB:
Pitch=(vcosθ)(2πmqB)
- Therefore, the final expression for the distance moved by the particle along the magnetic field in one rotation is:
Pitch=2πmvcosθqB
- The magnetic field →B is directed along the x-axis.
- The particle has a charge q and mass m, and it enters the magnetic field with a velocity →v at the origin in the x-y plane.
- The velocity can be resolved into two components:
- vx=vcosθ (component along the x-axis, parallel to →B)
- vy=vsinθ (component along the y-axis, perpendicular to →B)
- The component of the velocity vy will cause the particle to move in a circular motion due to the magnetic force acting on it.
- The component vx will cause the particle to move linearly along the x-axis.
- The combination of these two motions results in a helical trajectory.
- The radius r of the circular motion can be determined using the centripetal force provided by the magnetic force:
F=qvyB=mv2yr
- Rearranging gives:
r=mvyqB
- Substituting vy=vsinθ:
r=m(vsinθ)qB
- The time period T for one complete rotation in the magnetic field can be derived from the circular motion:
T=2πrvy
- Substituting the expression for r:
T=2π(m(vsinθ)qB)vsinθ=2πmqB
- The distance moved along the x-axis (the pitch of the helix) during one complete rotation is given by:
Pitch=vx⋅T
- Substituting vx=vcosθ and T=2πmqB:
Pitch=(vcosθ)(2πmqB)
- Therefore, the final expression for the distance moved by the particle along the magnetic field in one rotation is:
Pitch=2πmvcosθqB
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section -D3videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section -E6videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section B4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
 View Solution
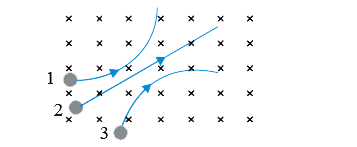
View SolutionParticles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
 View Solution
View SolutionA proton is moved along a magnetic field line.The magnetic force on the particle is
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionDefine one tesla using the expression fo the magnetic force acting on a particle of charge .q. moving with velocity →v in a magnetic field →B.
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
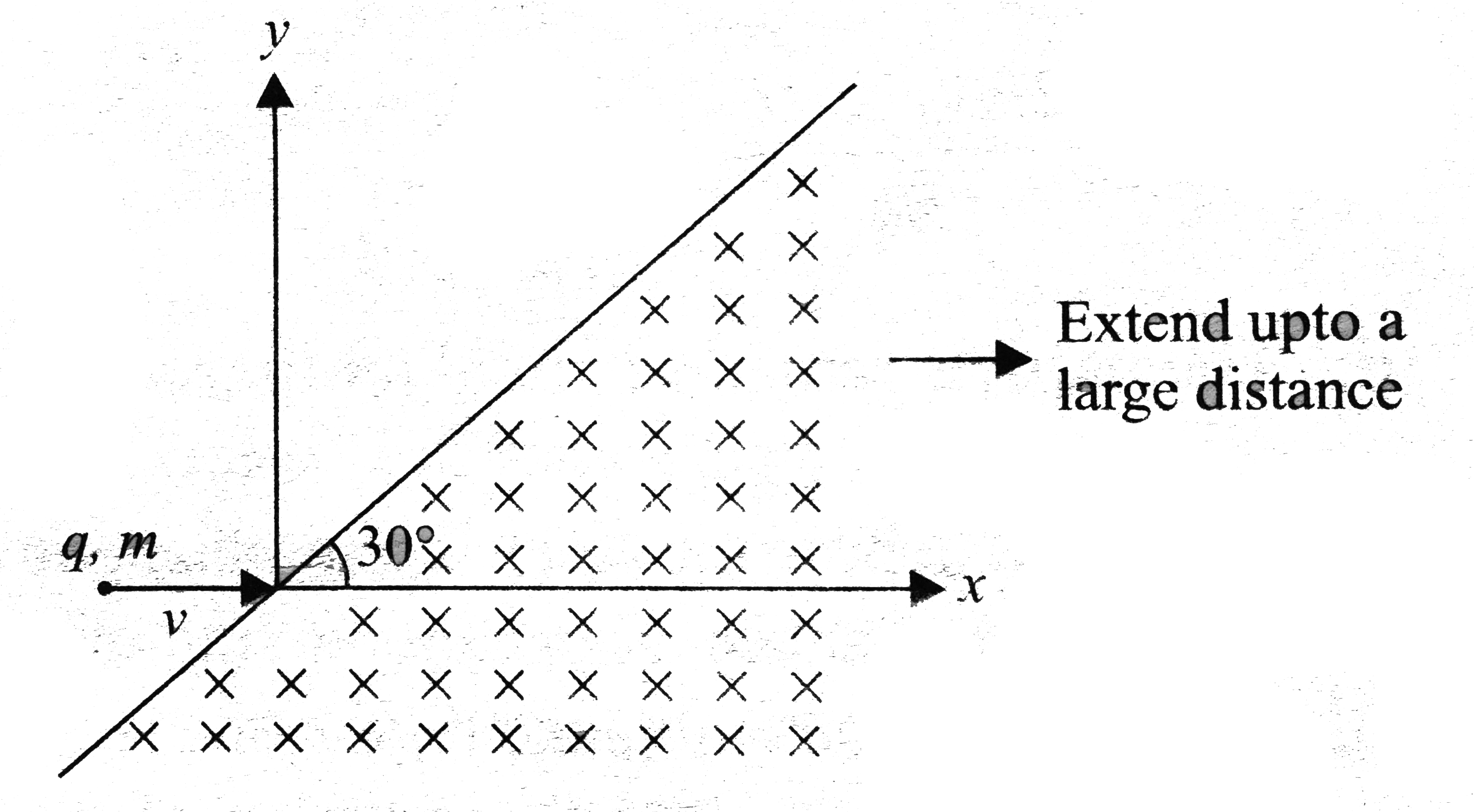 View Solution
View Solution
