A charged point particle having positive charge $q$ , mass $m$ is projected in $x - z$ plane with a speed $v_{0}$ at an angle $θ$ with the $x - axis$ , while another identical particle is projected simultaneously along the $y - axis$ from the origin (see figure) with an equal speed $v_{0}$ .
An electric field $\to E = - E_{0} ˆ k$ exists in the $x - z$ plane, while a magnetic field $\to B = B_{0} ˆ k$ exists in the region $y > 0$ ( $F_{0}$ , $B_{0} > 0$ ). It is observed that both the particles collide after some time. Assume that the space is gravity free.
( $i$ ) Find the time after which the particles collide and the coordinates of the point of collision.
( $i i$ ) Find the velocity $v_{0}$ and the angle $θ$ in terms of the other variables.
( $i i i$ ) What is the maximum value of the $z -$ coordinate of the first particle ?

Video Solution

Text Solution

Verified by Experts

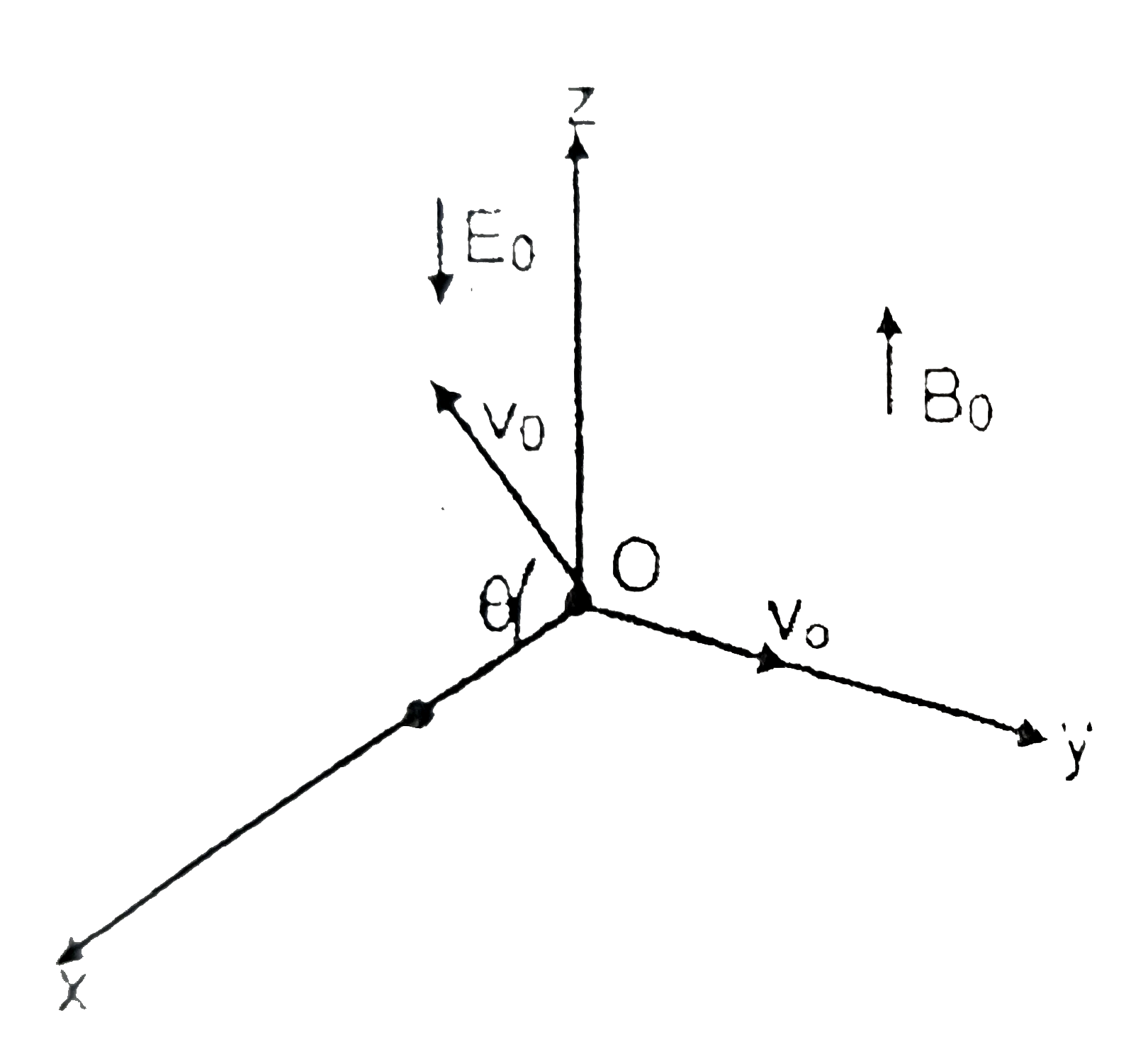
The acceleration on the charge $q$ , projected along the $x - z$ palne is along the $- z$ direction.
$a = \frac{q E_{0}}{m}$
The second particle moves on the $x - y$ plane in a circle of radius $R$ (say) such that :
$2 R = \frac{2 v_{0}^{2}}{a} sin θ cos θ$ .......( $i$ )
Also, $R = \frac{m v_{0}}{q B_{0}}$ .....( $i i$ )
$T = \frac{2 v_{0} sin θ}{a}$ ......( $i i i$ )
& $T = \frac{π m}{q B_{0}}$ .....( $i v$ )
where $T$ is the time required for the collision to occur
By solving, $v_{0} sin θ cos θ = \frac{E_{0}}{B_{0}}$
Also, $v_{0} sin θ = \frac{π}{2} \frac{E_{0}}{B_{0}}$
$\Rightarrow cos θ = \frac{2}{π}$ , $θ = {cos}^{- 1} (\frac{2}{π})$ , $v_{0} = \frac{E_{0} / B_{0}}{\frac{2}{π} \sqrt{1 - 2^{2} / π^{2}}}$
The maximum value of the $Z$ -coordinate of the first particle is
$H = \frac{v_{0}^{2} {sin}^{2} θ}{2 a} = \frac{π^{2}}{8} \frac{m E_{0}}{q B_{0}^{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile