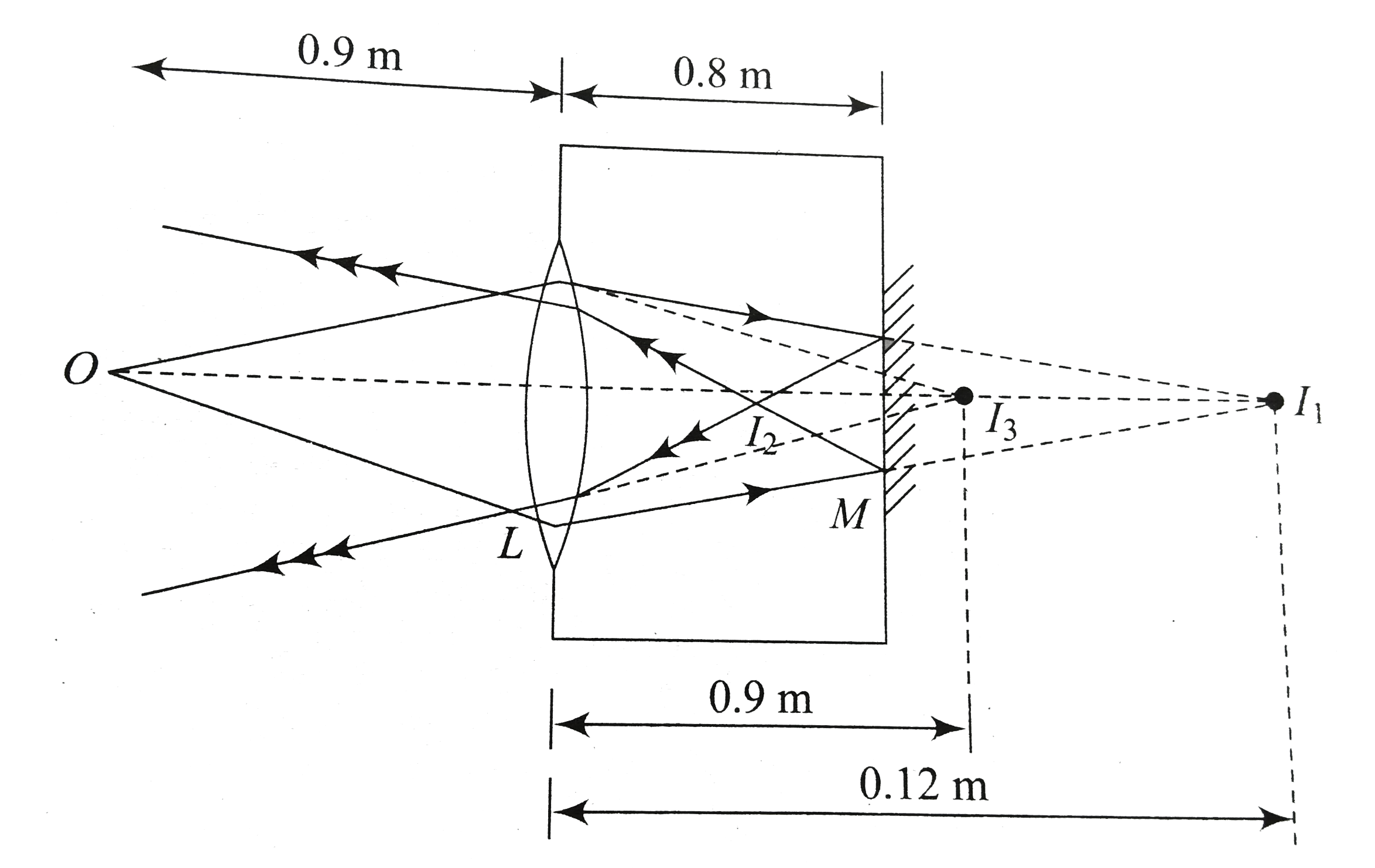
A thin equiconvex lens made of glass of refractive index 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (μ=32). On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance oa 0.9m from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

If R is radius of curvature of each lens surface, then for air on either side of lens, we have
1f=(.aμg−1)(1R1−1R2)=(32−1)(1R+1R)
⇒1f=1R⇒f=R⇒R=F=0.3m
If μ2 is refractive index of lens material and μ1,μ2 are refractive indices on either side of the lens, then the formula is
μ3v−μ1μ=μ2−μ1R1+μ3−μ2R2
Here R1=0.3m,R2=−0.3m,μ1=μair=1 ,
μ2=μglass=32,μ3=μwater=43,u=−9m,v=?
∴4/3v−1(−0.9)=(32−1)0.3+(43−32)−0.3
or 43v+10.9=10.6+11.8
or 43v=10.6+11.8=10.9=10.9
or v=0.9×43=1.2m
That is imageI1 is at a distance 1.2m from lens L to the right or at a distance (1.2−0.8)=0.4m to the right of mirror M. This image I1 acts as a virtual source for the plane mirror and forms real image I1 at a distance 0.4m on to the left of mirror and hence at a distance (0.8−0.4)=0.4m to the right of convex lens. This image I2 acts as an object for the lens.
Again, the formula if
μ′2v''−μ′1μ''=μ′2−μ′1R1+μ′3−μ′2R2
But now
μ′1=μwater=43,μ′3=μglass=32,μ′2=μair=1
R1=−0.3m,R2=+0.3m,u''=0.4m,v''=?
∴1v''−10.3=−11.8−10.6
or 1v''=10.3−11.8−10.6=10.9⇒v''=0.9m
That is image I3 is formed to the right at a distance 0.9m from the lens and is virtual. That is position of final iamge will be 0.9m to the right of lens.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionA thin lens made of glass of refractive index μ=1.5 has a focal length equal to 12 cm in air. It is now immersed in water (μ=43). Its new focal length is
View SolutionA thin equi-convex lens is made of glass of refractive index 1.5 and its length is 0.2m. If it acts as a concave lens of 0.5m focal length when dipped in a liquid, the refractive index of the liquid is
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the first image after refraction from the lens.
View SolutionAn equiconvex lens of glass (μg=1.5) of focal length 10 cm is silvered on one side. It will behave like a
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the second image after reflection from the mirror.
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

As in the lat problem, find the distance of A' below the optic axis of lens.
View SolutionA lens of refractive index n is put in a liquid of refractive index n'. If focal length of lens in air is f, its focal length in liquid will be.
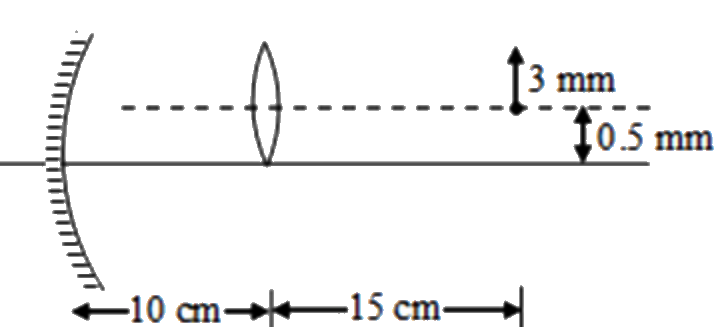
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placedon the optic axis of lens at a distnace between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
View Solution
