A large glass slab (μ=5/3) of thickness 8cm is placed over a point source of light on a plane surface. It is seen that light emerges out of the top surface of the slab from a circular area of radius R cm. What is the value of R?
The correct Answer is:6
To solve the problem, we need to find the radius R of the circular area from which light emerges from the top surface of a glass slab. The given parameters are:
- Refractive index of the glass slab, μ=53
- Thickness of the slab, t=8 cm
1. Understanding the Geometry:
- The light source is at the bottom of the slab, and the light rays will emerge from the top surface of the slab. The angle of incidence at the bottom surface will determine how wide the emerging light will spread out.
2. Using Snell's Law:
- According to Snell's Law, when light travels from one medium to another, the relationship between the angles and the refractive indices is given by:
μ1sini=μ2sinr
- Here, μ1=1 (for air), μ2=53 (for glass), i is the angle of incidence, and r is the angle of refraction.
3. Finding the Critical Angle:
- The critical angle C can be found when light travels from glass to air (where it will refract at 90∘):
53sinC=1⋅sin90∘
- This simplifies to:
sinC=35
- Therefore, the critical angle C is:
C=arcsin(35)≈37∘
4. Using Geometry to Relate R and Thickness:
- From the geometry of the situation, we can relate the radius R of the circular area to the thickness of the slab using the tangent of the angle C:
tanC=Rt
- Substituting t=8 cm:
tan37∘=R8
5. Finding tan37∘:
- The value of tan37∘ is known to be approximately 34:
34=R8
6. Solving for R:
- Cross-multiplying gives:
3⋅8=4R
- Simplifying this:
24=4R⟹R=244=6 cm
Final Answer:
The value of R is 6 cm.
---
- Thickness of the slab, t=8 cm
- The light source is at the bottom of the slab, and the light rays will emerge from the top surface of the slab. The angle of incidence at the bottom surface will determine how wide the emerging light will spread out.
- According to Snell's Law, when light travels from one medium to another, the relationship between the angles and the refractive indices is given by:
μ1sini=μ2sinr
- Here, μ1=1 (for air), μ2=53 (for glass), i is the angle of incidence, and r is the angle of refraction.
- The critical angle C can be found when light travels from glass to air (where it will refract at 90∘):
53sinC=1⋅sin90∘
- This simplifies to:
sinC=35
- Therefore, the critical angle C is:
C=arcsin(35)≈37∘
- From the geometry of the situation, we can relate the radius R of the circular area to the thickness of the slab using the tangent of the angle C:
tanC=Rt
- Substituting t=8 cm:
tan37∘=R8
- The value of tan37∘ is known to be approximately 34:
34=R8
- Cross-multiplying gives:
3⋅8=4R
- Simplifying this:
24=4R⟹R=244=6 cm
The value of R is 6 cm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig Type2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A glass slab (μ=1.5) of thickness 6 cm is placed over a paper. What is the shift in the letters?
View SolutionA flat glass slab of thickness 6cm and index 1.5 is placed in front of a plane mirror. An observer is standing behind the glass slab and looking at the mirror. The actual distance of the observer from the mirror is 50cm. The distance of his image from himself, as seen by the observer is
View SolutionA glass slab of thickness 12 cm is placed on a table. The level surface of the slab has a black spot. At what depth from the upper surface will the spot appear when viewed from above?
(Refractive index of glass = 1.5)View SolutionA ray of light strikes a glass slab (R.l. = μ) of finite thickness t. The emerging light is
View SolutionA rod of glass (μ=1.5) and of square cross section is bent into the shape shown in the figure. A parallel beam of light falls on the plane flat surface A as shown in the figure. If d is the width of a side and R is the radius of circular arc then for what maximum value of dR light entering the glass slab through surface A emerges from the glass through B
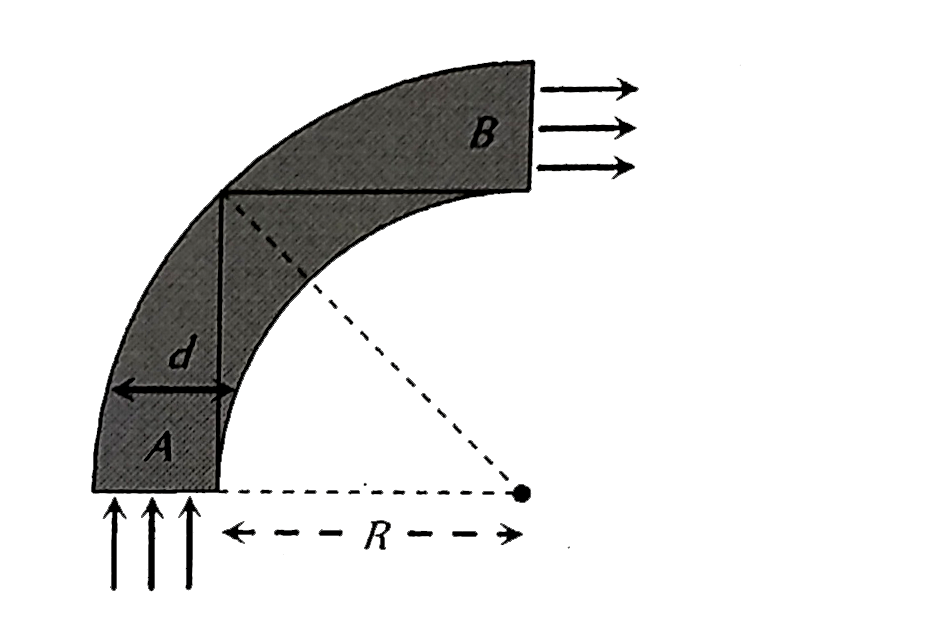 View Solution
View SolutionA disc is placed on a surface of pond which has refractive index 35 . A source of light is placed 4 m below the surface of liquid. The minimum radius of disc will be so light is not coming out
View SolutionA glass slab of thickness 4cm contains the same number of waves as 5cm of water, when both are traversed by the same monochromatic light. If the refractive index of water is 4/3, then refractive index of glass is
View SolutionAssertion A diverging lens (in air) cannot be made more diverging whatever be the medium we choose completely immerse the lens.
Reason The minimum refractive index of any medium is 1.View SolutionA plane mirror is made of glass slab (μg=1.5) 2.5 cm thick and silvered on back. A point object is placed 5 cm in front of the unsilvered face of the mirror. What will be the position of final image ?
View SolutionThe refractive index of a material changes by 0.014 as the colour of the light changes from red to violet. A rectangular slab of height 2.00 cm made of this material is placed on a newspaper. When viewed normally in yellow light, the letters appear 1.32 cm below the top surface of the slab. Calculate the dispersive power of the material.
View Solution
