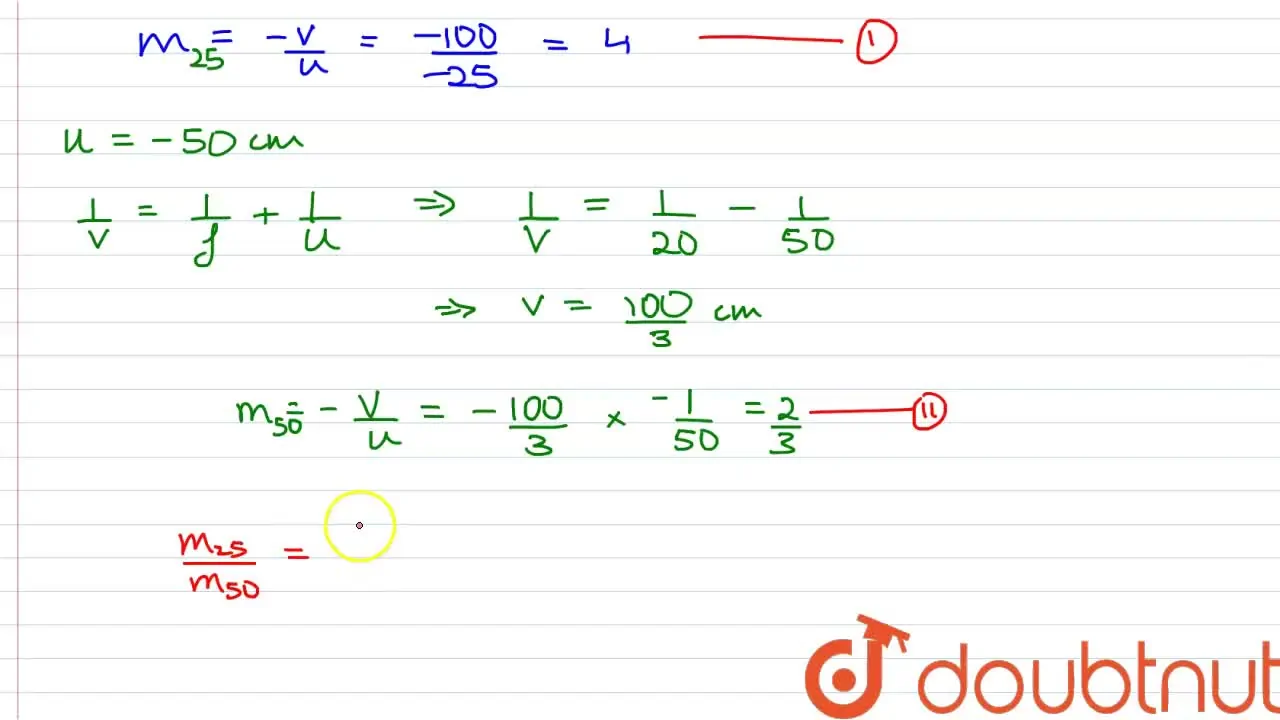
The focal length of a thin biconvex lens is 20cm. When an object is moved from a distance of 25cm in front of it to 50cm, the magnification of its image changes from to . The ration is
The correct Answer is:6
m=(f)/(f+u)
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig Type2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
The focal length of a concave mirror is 50cm. Where an object be placed so that its image is two times and inverted
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View SolutionIf a lens is moved towards the object from a distance of 40 cm to 30 cm, the magnification of the image remains the same (numarically). The focal length of the lens is
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.View SolutionAn object of height 2 cm is placed in front of a convex lens of focal length 20 cm at a distance of 15 cm from it. Find the position and magnification of the image.
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.View SolutionThe focal length of a simple convex lens used as a magnifier is 10 cm. For the image to be formed at a distance of distinct vision D = 25 cm, the object must be placed away from the lens nearly at a distance of
View SolutionAn astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.Then the magnification
View SolutionDraw a labelled ray diagram for the formation of image by a convex lens of focal length 15 cm when the object is placed at a distance of 25 cm from the lens. Determine the size of the image formed, if size of the object is 4 cm.
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View Solution