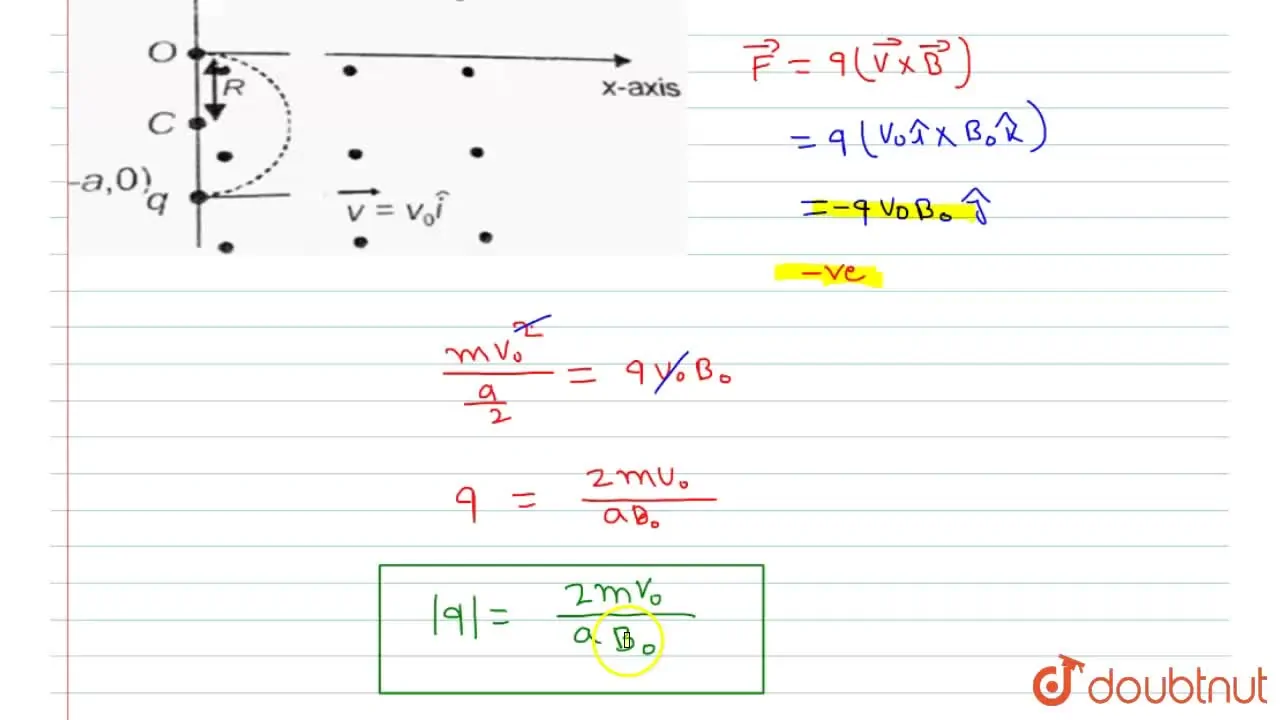
There exists a uniform magnetic field →B=+B0ˆk for x>0and→B=0 for all x<0. A charged particle placed at (0,−a,0) is given an initial velocity →v=v0ˆi. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at (0,−a,0) must be towards y-axis
→F=q(→v×→B)
⇒→F=q(v0ˆi×B0ˆk)=−qv0Bˆj
⇒ q must be negative
Let C be the centre of the circle
such that R=a2
mv0|q|B0=a2
∴q=−2mv0B0a
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration14videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself27videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
Similar Questions
If an electron is not deflected in passing through a certain region of space can we be sure that there is no magnetic field in that region?
02:58View SolutionAn α-particle of mass 6.65×10−27kg is travelling at right angles to a magnetic field with a speed of 6×105ms−1. The strength of the magnetic field is 0.2T. Calculate the force on the α-particle and its acceleration.
07:13View SolutionThe magnetic field produced around a straight line wire when current flows through it is
04:11View SolutionA : Uncertainty principle demands that an electron confined to a nucleus must have very high energy so that the electron cannot reside in a nucleus.
R: The electrostatic attraction between electron and proton is large at such a small distance but is not enough to bind such a high -energy electron.02:50View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 03:36View Solution
03:36View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
08:45View SolutionIn uniform magnetic field, if angle between vec(v) and vec(B) is 0^(@) lt 0 lt 90^(@) , the path of particle is helix. Let v_(1) be the component of vec(v) along vec(B) and v_(2) be the component perpendicular to vec(B) . Suppose p is the pitch. T is the time period and r is the radius of helix. Then T = (2pim)/(qB), r = (mv_(2))/(qB), P = (v_(1))T Assume a charged particle of charge q and mass m is released from the origin with velocity vec(v) = v_(0) hat(i) - v_(0) hat(k) in a uniform magnetic field vec(B) = -B_(0) hat(k) . Pitch of helical path described by particle is
11:57View SolutionTwo charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field vec(B)=B_(0)hat(K)
View SolutionElectric field strength bar(E)=E_(0)hat(i) and bar(B)=B_(0)hat(i) exists in a region. A charge is projected with a velocity bar(v)=v_(0)hat(j) at origin , then
05:28View SolutionIn region x gt 0 a uniform and constant magnetic field vec(B)_(1) = 2 B_(0) hat(k) exists. Another uniform and constant magnetic field vec(B)_(2) = B_(0) hat(k) exists in region x lt 0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity bar(u) = u_(0) hat(i) . The particle comes back to its initial position after a time : ( B_(0),u_(0) are positive constants)
13:06View SolutionA particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
05:20View SolutionAssertion In a uniform magnetic field B=B0ˆk, if velocity of a charged particle is v0ˆi at t = 0, then it can have the velocity v0ˆj at some other instant.
Reason In uniform magnetic field, acceleration of a charged particle is always zero.04:09View SolutionThere exists a uniform magnetic field →B=+B0ˆk for x>0and→B=0 for all x<0. A charged particle placed at (0,−a,0) is given an initial velocity →v=v0ˆi. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at (0,−a,0) must be towards y-axis06:42View SolutionA particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk06:11View SolutionTwo charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field vec(B)=B_(0)hat(K)
01:32View Solutionएक इलेक्ट्रॉन प्रारंभिक वेग →v=v0ˆi से गति कर रहा है तथा चुम्बकीय क्षेत्र →B=B0ˆj में है , तो इसकी दे ब्रोग्ली तरंगदैर्घ्य
03:25View Solution