In region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
32πmqB0
2πmqB0
3πmqB0
Particle does not come back to its initial position
The correct Answer is:B
The motion of positively charged particle in the given combination of magnetic field will be as shown. The particle comes back to its initial position after covering three half circles.
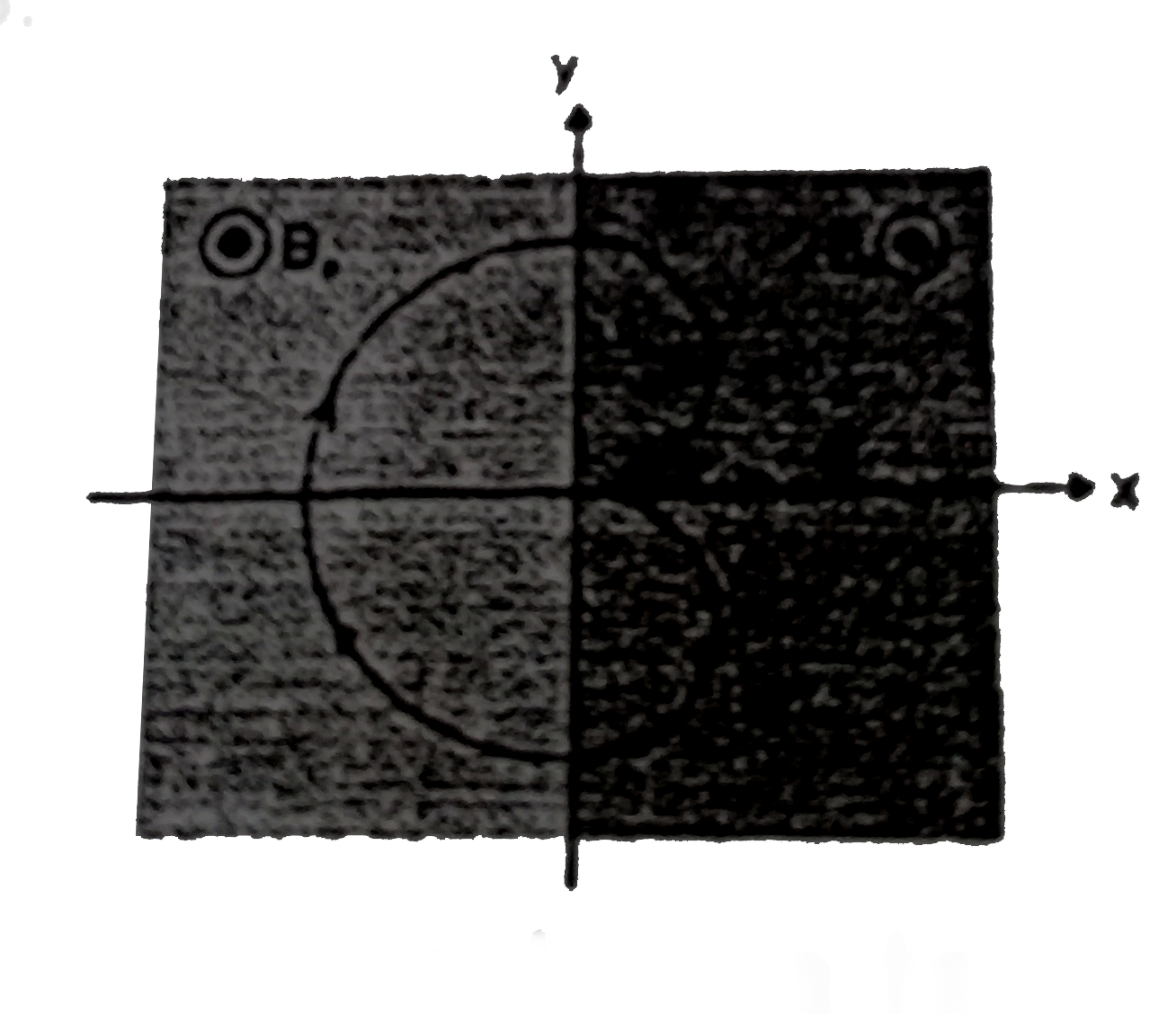
Hence net time taken to come back to initial position is
T=πm2qB0+πmqB0+πm2qB0=2πmqB0
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.48
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.49
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.46
Explore 11 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
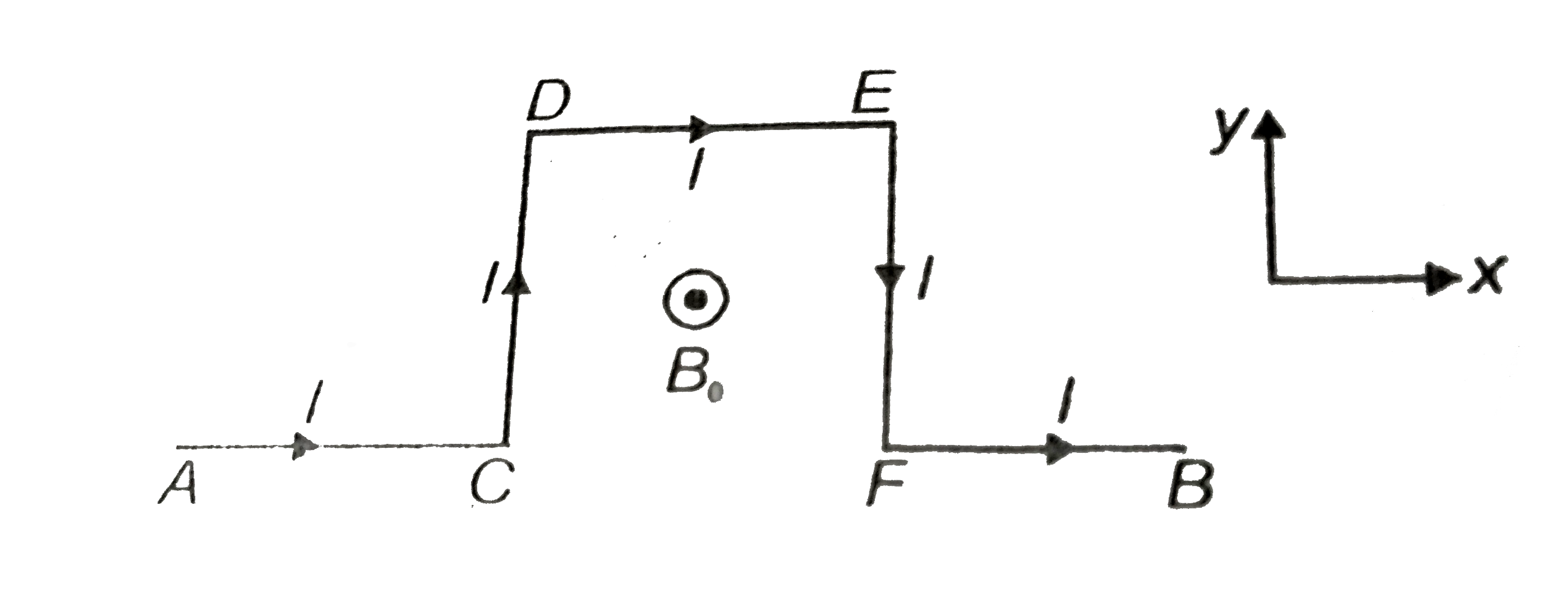
A uniform magnetic field →B=B0ˆk exists in a region. A current carrying wire is placed in x-y plane as show. Find the force acting on the wire AB, if each section of the wire is of length 'a'.
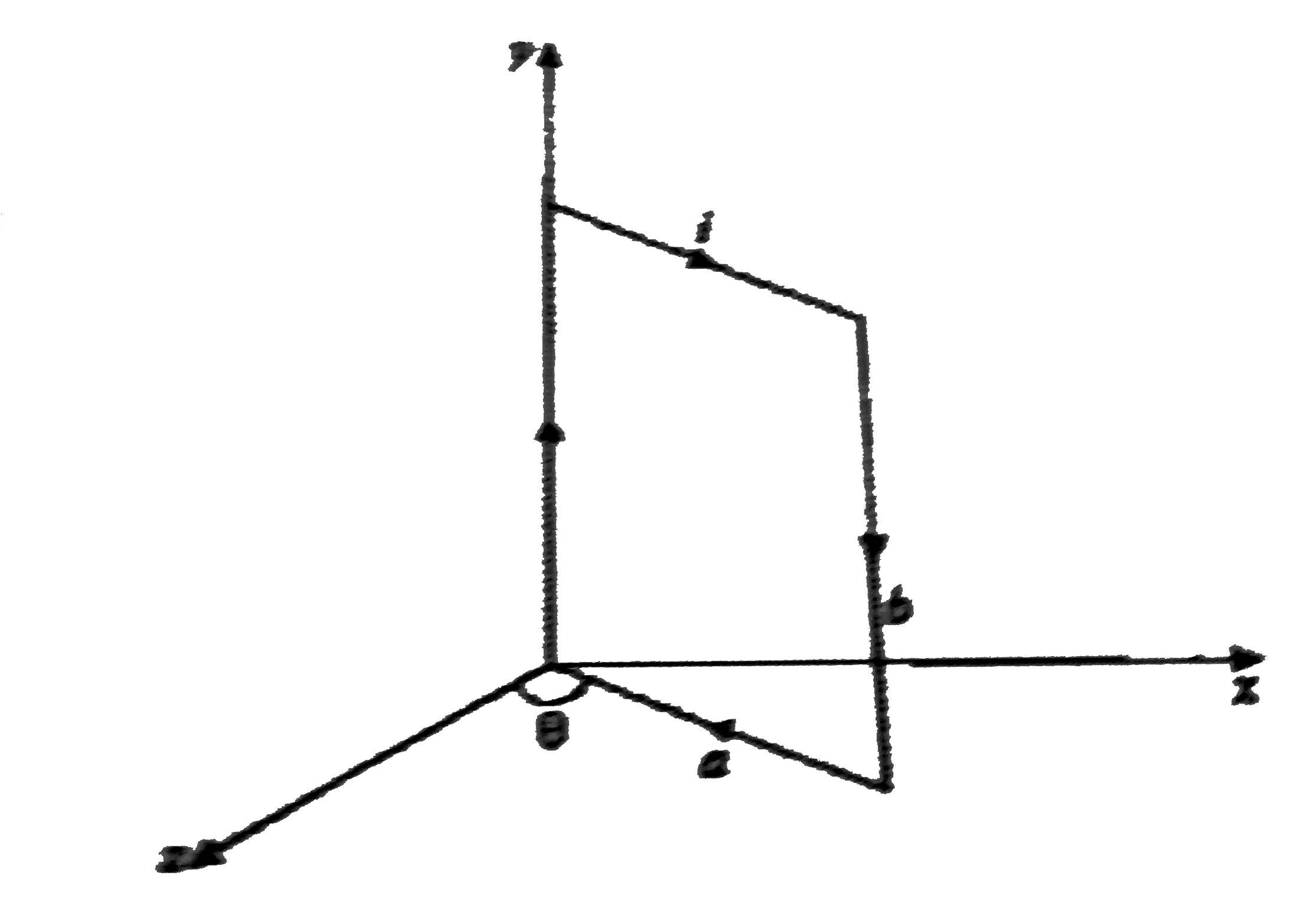
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View Solution
Knowledge Check
A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
Aits z co-ordinate can never be negativeBits x co-ordinate can never be positiveCits x and z co-oridinate cannot be zero at the same timeDits y co-ordinate will be proportional to its time of flightA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 A
A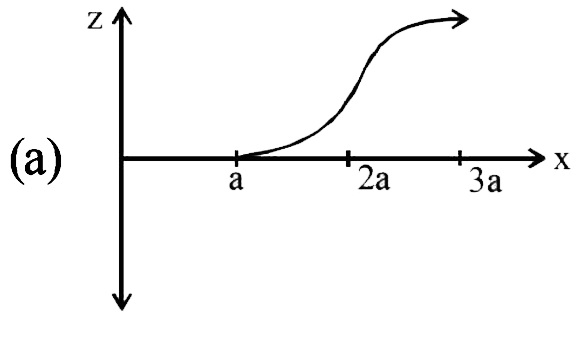 B
B C
C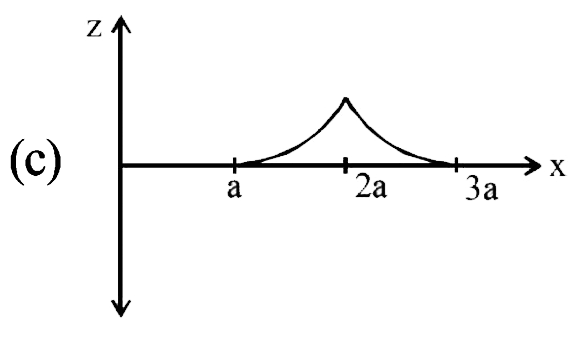 D
D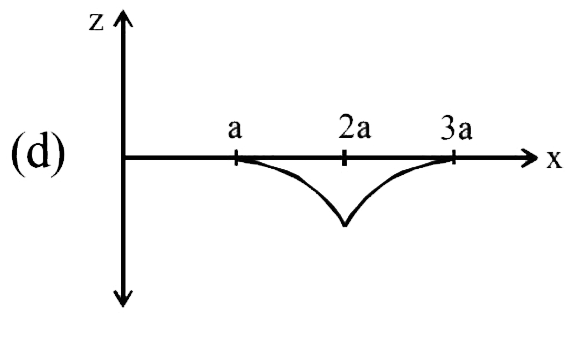
A magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
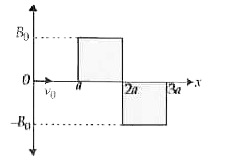
the magnetic field at x=a, The trajectory of the charge in this region can be like,A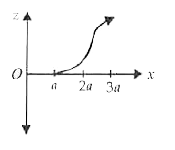 B
B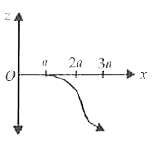 C
C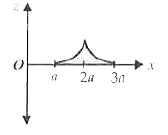 D
D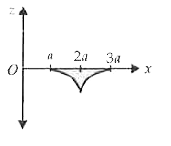
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.

View SolutionA conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
View SolutionIn a region at a distance r from z-axis, magnetic field →B=B0rtˆk is present where B0 is constant and t is time. Then the magnetic of induced electric field at a distance r from z-axis is given by
View SolutionA charged particle of specific charge (charge/mass) α released from origin at time t=0 with velocity →v=v0(ˆi+ˆj) in uniform magnetic field →B=B0ˆi. Coordinates of the particle at time t=π/(B0α) are
View Solution

