Electric field strength ¯¯¯E=E0ˆi and ¯¯¯B=B0ˆi exists in a region. A charge is projected with a velocity ¯v=v0ˆj at origin , then
It moves along helix with constant pitch
It moves along circular path in YZ plane
It moves along helix with increasing pitch
It moves along helix with decreasing pitch
The correct Answer is:3
It moves along a circular path in YZ plane due to ¯¯¯B and along a straight line path due to →E . This combination is helix but with increasing pitch.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-VI (SINGLE ANSWER QUESTION)
Explore 81 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-III
Explore 45 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
Electric field and magnetic field in a region of space are given by(Ē=E0ˆj). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View SolutionAn electric field →E=E0ˆi+E0ˆj exists in space. The flux through triangular loop with vertices at (a2,0,0), (a2,0,a) and (a2,a,a2) is E0a2b. Find b.
View Solution
Knowledge Check
Electric field strength ¯¯¯E=E0ˆi and magnetic induction ¯¯¯B=B0ˆi exists in a region. A charged particle 'q' is released from rest at origin. Work done by both the fields is after certain time is
AqExBqEyCqEzDqE√x2+y2A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
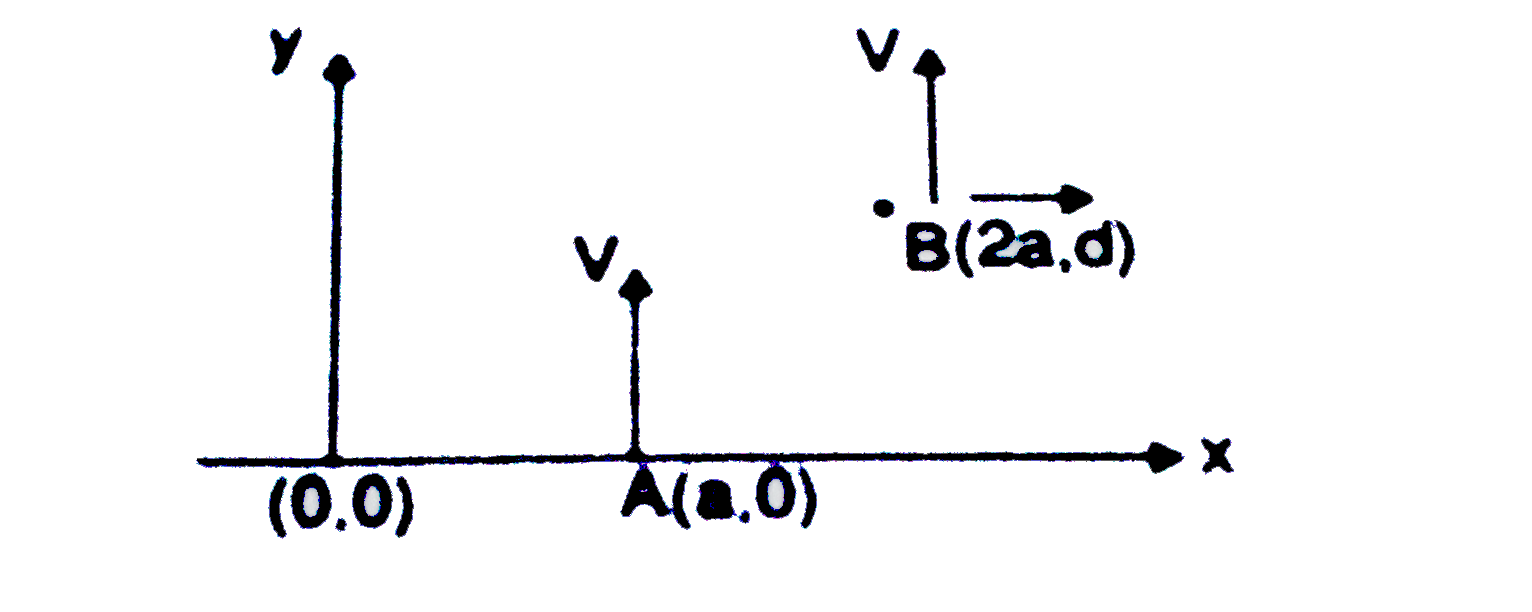 A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.
A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.In a certain region static electric and magentic fields exist. The magnetic field is given by →B=B0(ˆi+2ˆj−4ˆk). If a test charge moving with a velocity, →υ=υ0(3ˆi−ˆj+2ˆk) experience no force in that region, then the electric field in the region, in SI units, is-
A→E=−υ0B0(ˆi+ˆj+7ˆk)B→E=−υ0B0(3ˆi−2ˆj−4ˆk)C→E=υ0B0(14ˆj+7ˆk)D→E=−υ0B0(14ˆj+7ˆk)
An electron moving with a velocity V1=ˆims at a point in a magnetic field experiences a force bar(F)=(−eˆj) Newton where 'e' is the charge of the electron.If the electron moves with a velocity ¯¯¯V2=2ˆkms at the same point the force experienced by it is
View SolutionAn electron moving with a velocity V_(1)=hat im/s at a point in a magnetic field experiences a force bar(F)=(-ehat j) Newton where 'e' is the charge of the electron.If the electron moves with a velocity bar(V)_(2)=2hat km/s at the same point the force experienced by it is
View SolutionA particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk
View SolutionAssertion In a uniform magnetic field B=B0ˆk, if velocity of a charged particle is v0ˆi at t = 0, then it can have the velocity v0ˆj at some other instant.
Reason In uniform magnetic field, acceleration of a charged particle is always zero.
View SolutionElectric and magnetic field are directed as E0ˆi and B0ˆk, a particle of mass m and charge + q is released from position (0,2,0) from rest. The velocity of that particle at (x,5,0) is (5ˆi+12ˆj) the value of x will be
View Solution

