Two wires AO and OC carry equal currents i as shown in Fig. One end of both the wires extends to infinity. Angle AOC is α. The magnitude of magnetic field is point P on the bisector of these two wires at a distance r from point O is

μ0i2πrcot(α2)
μ0i4πrcot(α2)
μ0i2πr(1+cos(α)2)sin(α2))
μ0i4πrsin(α2)
The correct Answer is:C
B=μ04πIa[sin(90−θ/2)+sin90∘]×2
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT Based Questions
Explore 20 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level-II(C.W)
Explore 63 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
Two wires CO and OA carry equal currents I as shown in figure. One end of both the wires extends to infinity. Given ∠AOC=θ. What is the magnitude of magnetic field induction at a point P at a distance r from O lying on the bisector of angle θ.
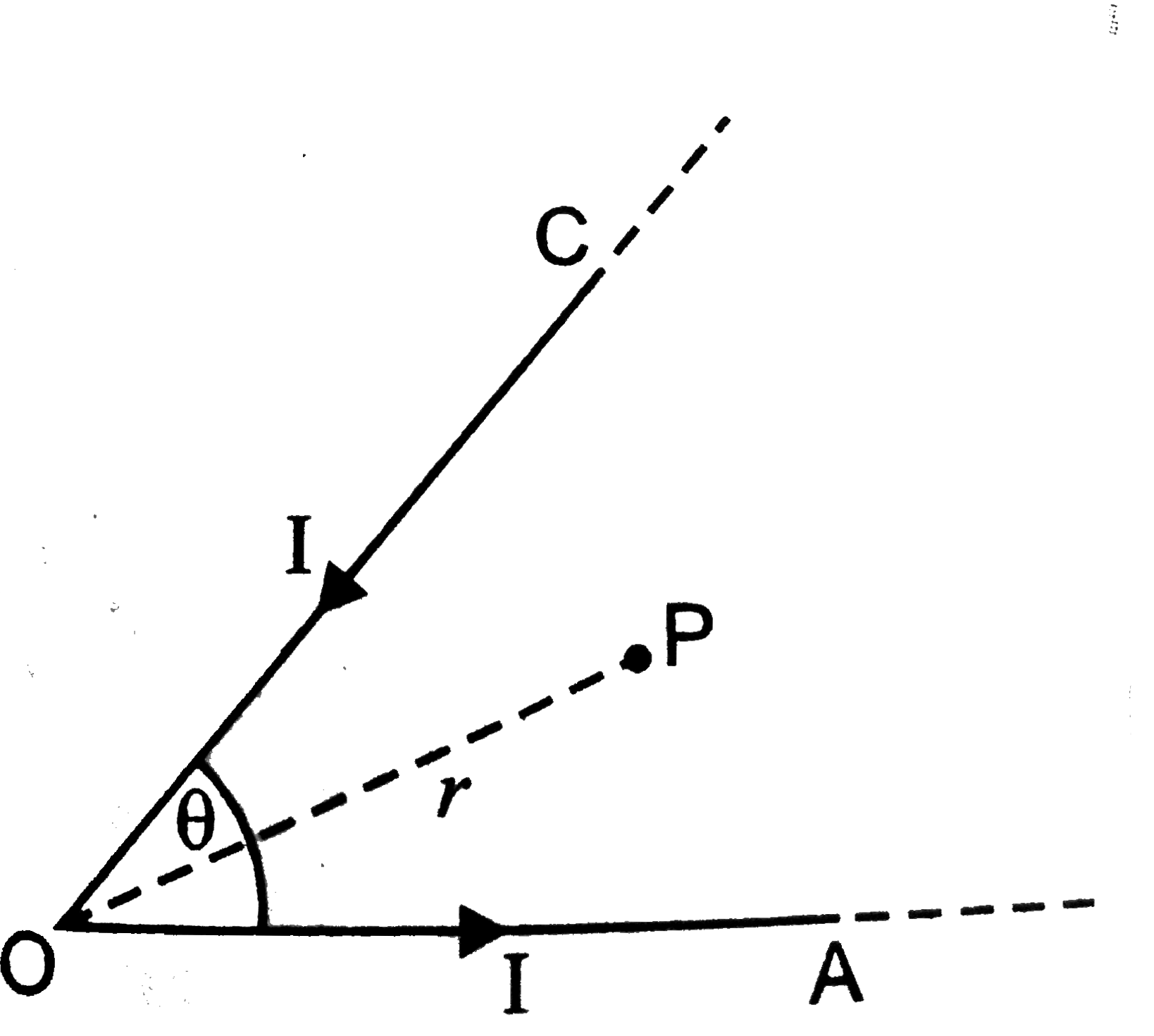
View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View Solution
Knowledge Check
A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
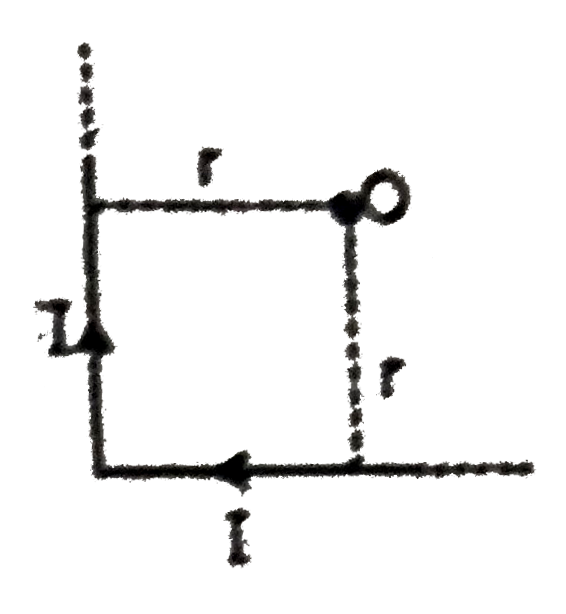 AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
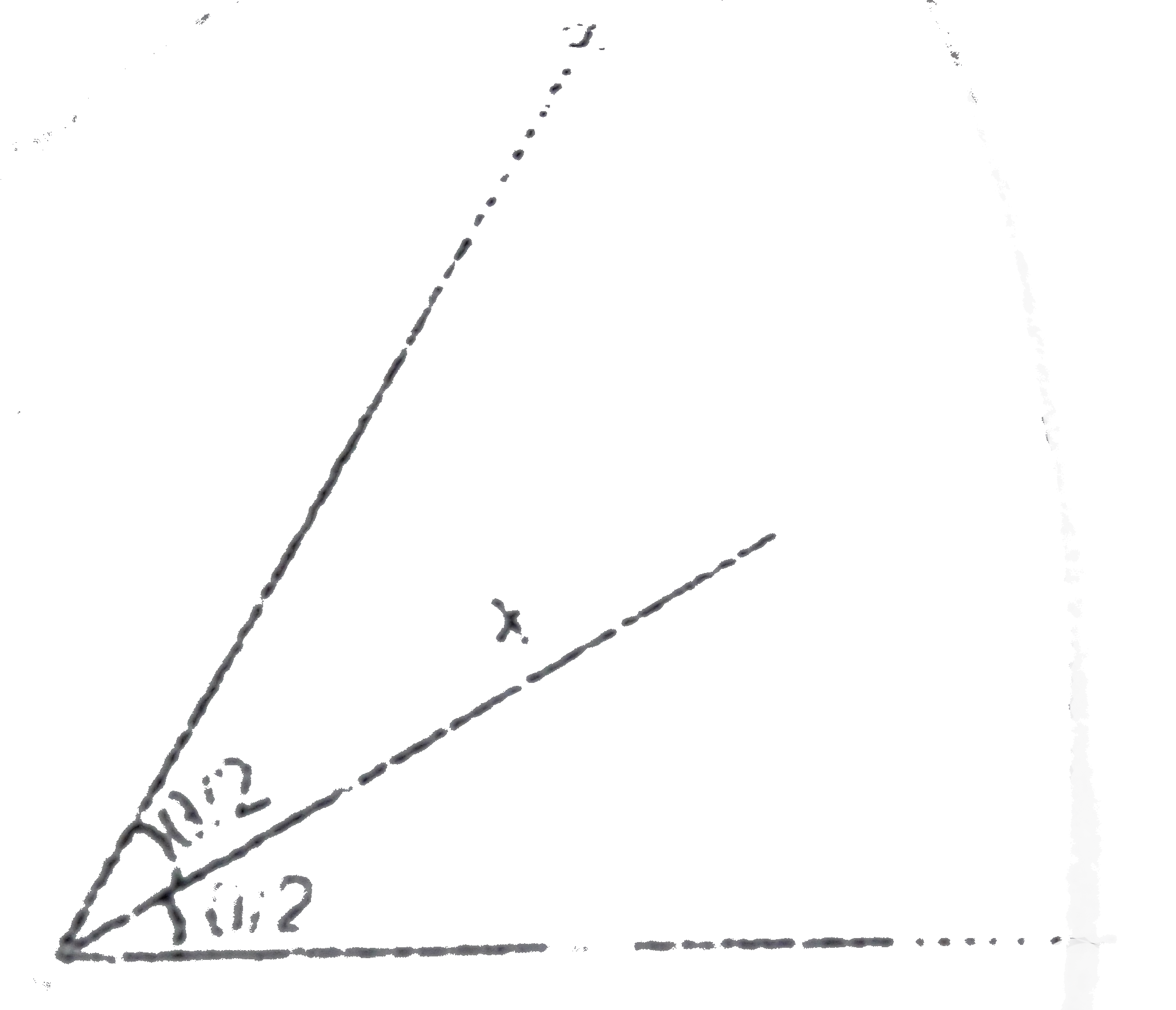 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
Alongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

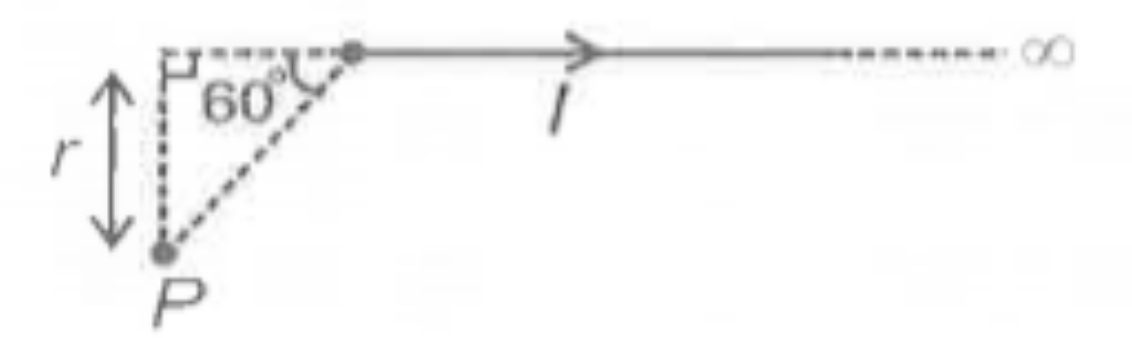
View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View Solution

