Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
μ0idπ(d2+x2)
μ0ixπ(d2−x2)
μ0ix(d2+x2)
μ0id(d2+x2)
The correct Answer is:B
To find the magnetic field B at a point P lying on the perpendicular line joining two long parallel wires carrying equal currents I in the same direction, we can follow these steps:
1. Identify the Configuration:
- We have two long parallel wires separated by a distance 2d.
- The point P is located at a distance x from the midpoint of the line joining the two wires.
2. Magnetic Field Due to a Single Wire:
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
3. Calculate the Distance from Each Wire:
- The distance from the first wire to point P is d−x.
- The distance from the second wire to point P is d+x.
4. Calculate the Magnetic Field at Point P:
- The magnetic field due to the first wire at point P (directed into the plane) is:
B1=μ0I2π(d−x)
- The magnetic field due to the second wire at point P (directed out of the plane) is:
B2=μ0I2π(d+x)
5. Determine the Net Magnetic Field:
- Since the currents are in the same direction, the magnetic fields will oppose each other. Thus, the net magnetic field B at point P is:
B=B1−B2=μ0I2π(d−x)−μ0I2π(d+x)
6. Combine the Terms:
- Factor out μ0I2π:
B=μ0I2π(1d−x−1d+x)
7. Simplify the Expression:
- To combine the fractions:
B=μ0I2π((d+x)−(d−x)(d−x)(d+x))
- This simplifies to:
B=μ0I2π(2xd2−x2)
- Therefore, the final expression for the magnetic field B at point P is:
B=μ0Ixπ(d2−x2)
- We have two long parallel wires separated by a distance 2d.
- The point P is located at a distance x from the midpoint of the line joining the two wires.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
- The distance from the first wire to point P is d−x.
- The distance from the second wire to point P is d+x.
- The magnetic field due to the first wire at point P (directed into the plane) is:
B1=μ0I2π(d−x)
- The magnetic field due to the second wire at point P (directed out of the plane) is:
B2=μ0I2π(d+x)
- Since the currents are in the same direction, the magnetic fields will oppose each other. Thus, the net magnetic field B at point P is:
B=B1−B2=μ0I2π(d−x)−μ0I2π(d+x)
- Factor out μ0I2π:
B=μ0I2π(1d−x−1d+x)
- To combine the fractions:
B=μ0I2π((d+x)−(d−x)(d−x)(d+x))
- This simplifies to:
B=μ0I2π(2xd2−x2)
- Therefore, the final expression for the magnetic field B at point P is:
B=μ0Ixπ(d2−x2)
Similar Questions
Two parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo long straight parallel wires A and B separated by a distance d, carry equal current I flowing in same direction as shown in the figure.
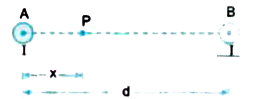
(a) Find the magnetic field at a point P situated between them at a distance x from one wire.
(b) Show graphically the variation of the magnetic field with distance x for 0<x<d.
View Solution
Knowledge Check
Two infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzeroTwo long parallel conducting wires carry current I in same direction, placed at distance b. Force per unit length of wire is
Aμ0I2πbBμ0I22πb2Cμ0I22πbDμ0I2πb2Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZero
A very long wire carrying a current I=5.0A A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance l=35cm from it.
View SolutionTwo parallel wires carrying currents I1 and I2 in opposite directions and separated by a distance d experience a
View SolutionTwo parallel wires carrying currents I1 and I2 in opposite directions and separated by a distance d experience a
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View Solution

