If an electron is not deflected in passing through a certain region of space can we be sure that there is no magnetic field in that region?
To determine whether we can be sure that there is no magnetic field in a region of space where an electron is not deflected, we can analyze the forces acting on the electron.
1. Understanding the Forces on a Charged Particle:
An electron is a charged particle and experiences forces when it moves through electric and magnetic fields. The force due to an electric field E is given by:
FE=qE
where q is the charge of the electron (which is negative).
2. Force Due to Magnetic Field:
The force acting on a charged particle moving in a magnetic field B is given by:
FB=q(v×B)
where v is the velocity of the electron.
3. Condition for No Deflection:
If the electron is not deflected, it means that the net force acting on it is zero. Therefore, we have:
FE+FB=0
This implies:
FE=−FB
4. Equating the Magnitudes of Forces:
The magnitudes of the electric and magnetic forces must be equal for the electron to travel in a straight line without deflection:
|qE|=|q(v×B)|
Since the charge q is the same for both forces, we can simplify this to:
|E|=|v×B|
5. Conclusion:
From the above analysis, we see that even if the electron is not deflected, it does not necessarily mean that there is no magnetic field present. It is possible that a magnetic field exists, but the force due to the electric field exactly balances the force due to the magnetic field, resulting in no net force and hence no deflection.
Final Answer:
No, we cannot be sure that there is no magnetic field in that region because the forces due to electric and magnetic fields could be equal and opposite, resulting in no net deflection of the electron.
---
An electron is a charged particle and experiences forces when it moves through electric and magnetic fields. The force due to an electric field E is given by:
FE=qE
where q is the charge of the electron (which is negative).
The force acting on a charged particle moving in a magnetic field B is given by:
FB=q(v×B)
where v is the velocity of the electron.
If the electron is not deflected, it means that the net force acting on it is zero. Therefore, we have:
FE+FB=0
This implies:
FE=−FB
The magnitudes of the electric and magnetic forces must be equal for the electron to travel in a straight line without deflection:
|qE|=|q(v×B)|
Since the charge q is the same for both forces, we can simplify this to:
|E|=|v×B|
From the above analysis, we see that even if the electron is not deflected, it does not necessarily mean that there is no magnetic field present. It is possible that a magnetic field exists, but the force due to the electric field exactly balances the force due to the magnetic field, resulting in no net force and hence no deflection.
No, we cannot be sure that there is no magnetic field in that region because the forces due to electric and magnetic fields could be equal and opposite, resulting in no net deflection of the electron.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Try Yourself
Explore 27 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Assignment (Section A) Objective Type Questions (One option is correct)
Explore 55 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Assignment Section J (Aakash Challengers Questions)
Explore 5 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
If a moving electron if deflected sideways in passing through a certain region of space, can we be sure that a magnetic field exists in that region?
View SolutionAn electron is not deflected an through a certain region because
View Solution(A) : If an electron is not deflected while passing through a certain region of space, then only possibility is that there is no magnetic field in this region
(R) : Force on an electron moving in a magnetic field is inversely proportional to the magnetic field applied.
View Solution(A) : If an electron is not deflected while passing through a certain region of space, then only possibility is that there is no magnetic field in this region.
(R) : Magnetic force on a charged particle is directly proportional to specific charge of particle.
View SolutionIf a beam of electrons travels in a straight line in a certain region. Can we say there is no magnetic field?
View SolutionAn electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field ?
View SolutionThe average electric field of electromagnetic waves in certain region of free space is 9×10–4NC–1. Then the average magnetic field in the same region is of the order of
View SolutionAssertion A beam of electron can pass undeflected through a region of E and B.
Reason Force on moving charged particle due to magnetic field may be zero in some cases.
View SolutionA beam consisting of protons and electrons moving at the same speed goes through athin region in which there is a magnetic field perpendicular to the beam. Protons and the electrons
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
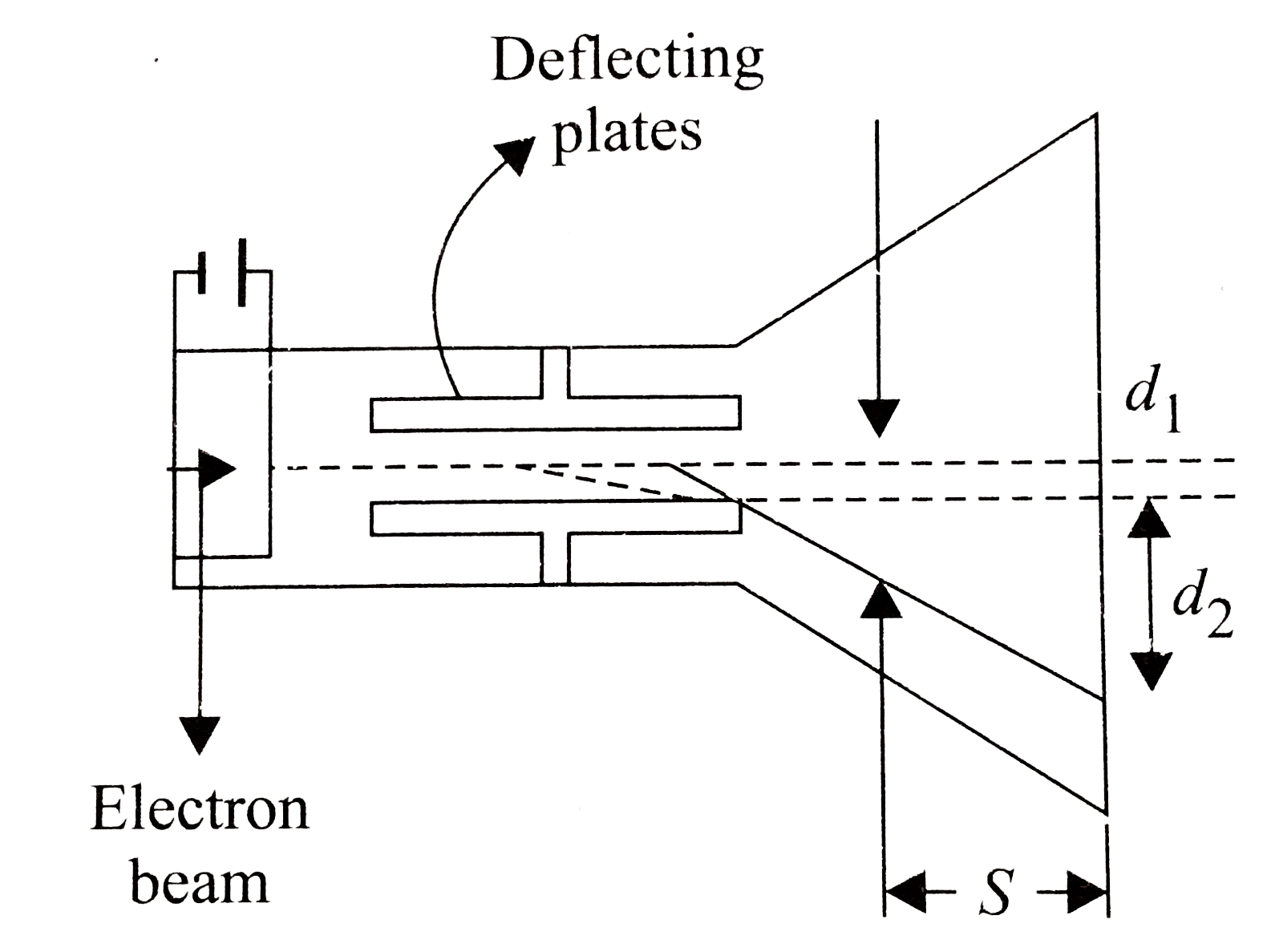
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View Solution

