Which of the following particles can't be accelerated in a cyclotron?
(1) Proton p+ (2) Antiproton p−
(3) Alpha particle α++ (4) Positron e+
To determine which of the following particles cannot be accelerated in a cyclotron, we need to consider the mass of the particles and the principles of how a cyclotron operates.
1. Understanding Cyclotron Operation: A cyclotron accelerates charged particles using a magnetic field and an alternating electric field. The effectiveness of this acceleration depends on the mass of the particle. Cyclotrons are particularly effective for particles with a mass that is not too small.
2. Analyzing the Options:
- Proton (p⁺): Protons have a relatively large mass compared to electrons. They can be effectively accelerated in a cyclotron.
- Antiproton (p⁻): Antiprotons have the same mass as protons (just opposite charge). Therefore, they can also be accelerated in a cyclotron.
- Alpha Particle (α²⁺): Alpha particles consist of two protons and two neutrons, giving them a mass greater than that of protons. They can also be accelerated in a cyclotron.
- Positron (e⁺): Positrons are the antimatter counterparts of electrons and have a very small mass, equal to that of electrons. Due to their very low mass, they cannot be effectively accelerated in a cyclotron.
3. Conclusion: Among the given options, the positron (e⁺) cannot be accelerated in a cyclotron due to its very small mass.
Final Answer: The particle that cannot be accelerated in a cyclotron is the Positron (e⁺).
---
- Proton (p⁺): Protons have a relatively large mass compared to electrons. They can be effectively accelerated in a cyclotron.
- Antiproton (p⁻): Antiprotons have the same mass as protons (just opposite charge). Therefore, they can also be accelerated in a cyclotron.
- Alpha Particle (α²⁺): Alpha particles consist of two protons and two neutrons, giving them a mass greater than that of protons. They can also be accelerated in a cyclotron.
- Positron (e⁺): Positrons are the antimatter counterparts of electrons and have a very small mass, equal to that of electrons. Due to their very low mass, they cannot be effectively accelerated in a cyclotron.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Try Yourself
Explore 27 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Assignment (Section A) Objective Type Questions (One option is correct)
Explore 55 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Assignment Section J (Aakash Challengers Questions)
Explore 5 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
Which of the following particle can be accelerated in cyclotron?
View SolutionThe increasing order (lowest first) for the values of e/m (charge/mass) for electron (e), proton (p), neutron (n), and alpha particle (α) is
View SolutionThe magnitude of the de-Broglie wavelength (λ) of an electron (e),proton(p),neutron (n) and α particle (a) all having the same energy of Mev, in the increasing order will follow the sequence:
View SolutionFor a given kinetic energy, which of the following has the smallest de Broglie wavelength : electron, proton and α−partic≤?
View SolutionWhich of the following path of α-particle is/are possible in the α-particle scattering experiment?
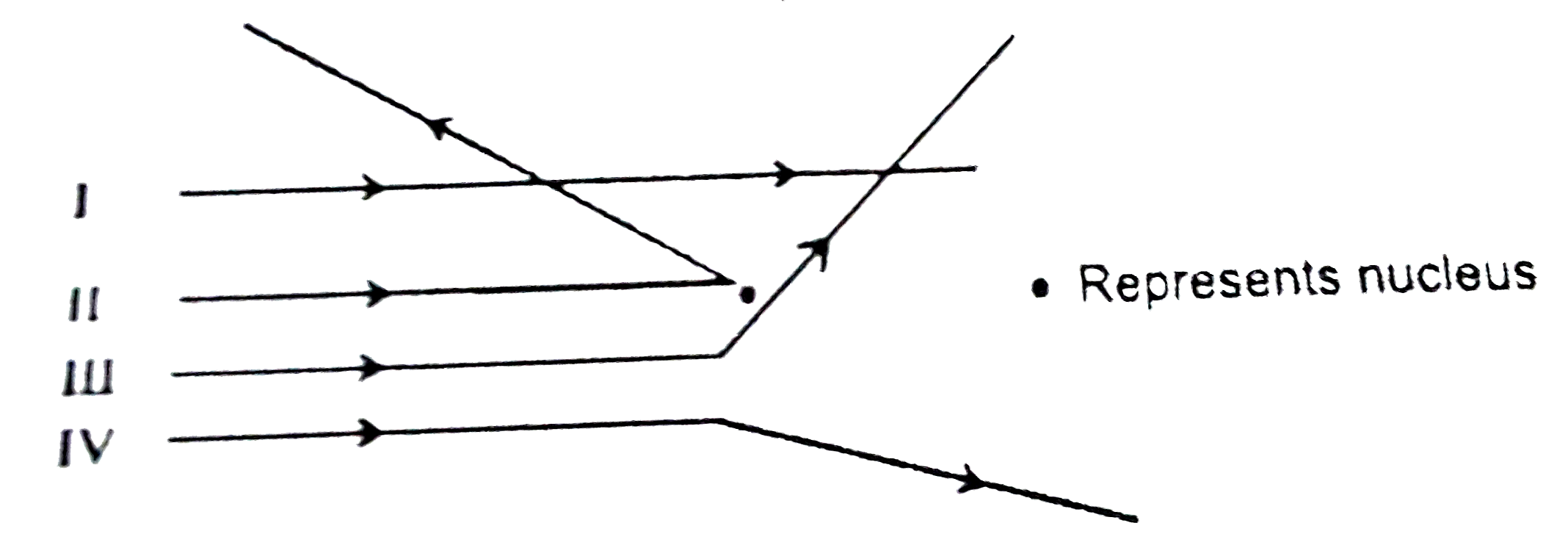
View SolutionFor which subatomic particle the ratio of charge and mass would be greater. (A) Proton, (B) Alpha particle, (C) Neutron, (D) Electron
View SolutionFor which of the following reaction the degree of dissociation (α) and equilibrium constant (Kp) are
related as Kp=4α2P(1−α2) ?
View SolutionAn α-particle is accelerated through a.p.d of 106 volt the K.E. of particle will be
View SolutionThe ration of spectific charge ( e//m) of a proton to that of an alpha-particle is :
View SolutionA particle of charge q and mass m moves rectilinearly under the action of an electric field E=α−βx. Here, αandβ are positive constants and x is the distance from the point where the particle was initially at rest. Then:
(1) the motion of the particle is oscillatory with amplitude αβ
(2) the mean position of the particles is at x=αβ
(3) the maximum acceleration of the particle is qαm
(4) All 1, 2 and 3
View Solution