A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as , where, k is a constant. Find an expression for the magnetic field B at a distance from the axis

Consider an Amperian loop of radius r as shown. The distribution of current shows that the field will be same everywhere on the Amperian loop
Now (by Ampere circuital law)
. To find current enclosed, consider a ring of radius x and thickness dx.
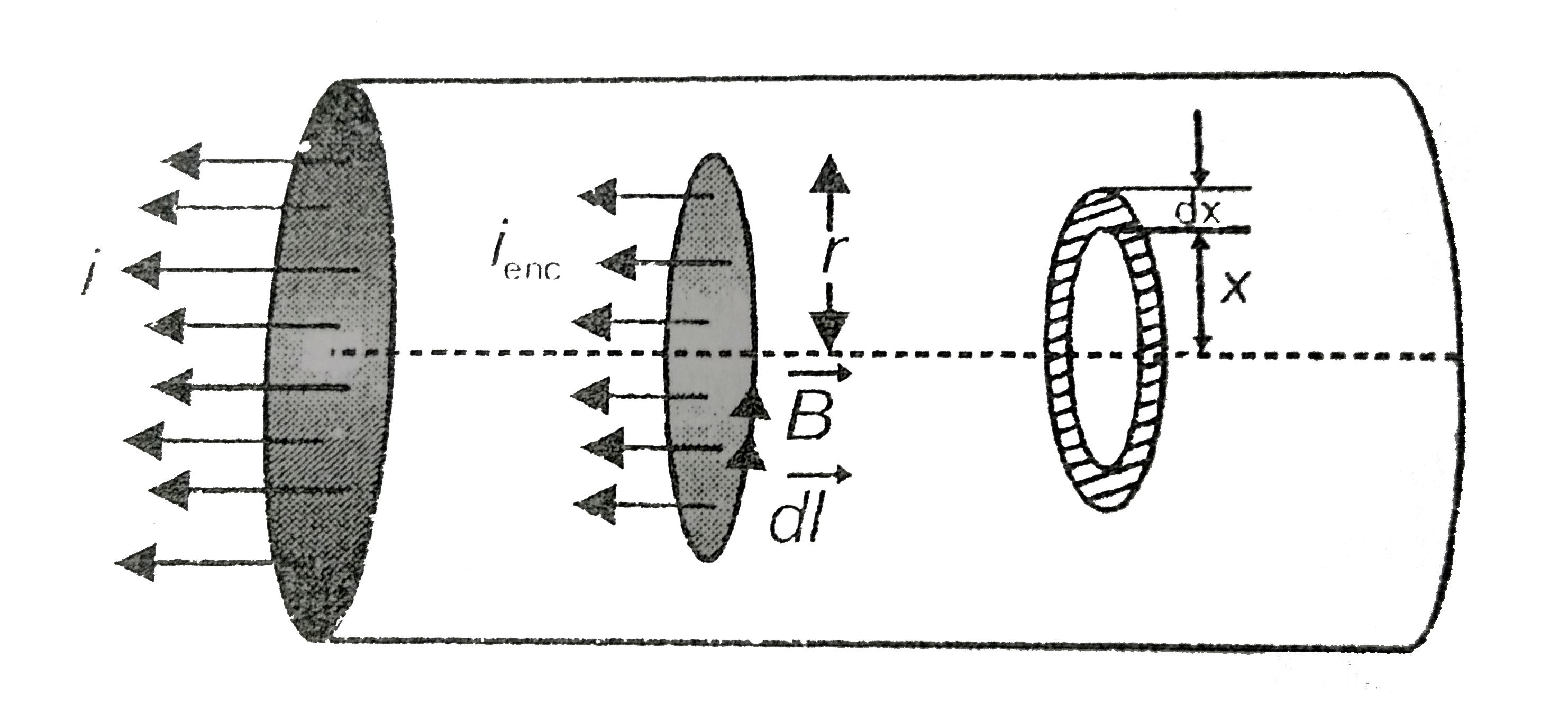
As
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
A long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
View SolutionA solid cylindrical conductor of radius R carries a current along its length.The current density J1 however, is not unifrom over the cross section of the conductor but is a function of the radius according to J=br, where b is a constant.the magnetic field B at r1<R is μ0br21N.Then find value of N
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionTwo large metal sheets carry surface currents as shown in figure . The current through a strip of width dl is Kdl where K is a constant . Find the magnetic field at the points P,Q and R.

View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
View SolutionAmpere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
View Solution
