A solid cylindrical conductor of radius R carries a current along its length.The current density J1 however, is not unifrom over the cross section of the conductor but is a function of the radius according to J=br, where b is a constant.the magnetic field B at r1<R is μ0br21N.Then find value of N
The correct Answer is:C
To solve the problem, we need to find the value of N in the expression for the magnetic field B at a distance r1 from the center of a solid cylindrical conductor carrying a non-uniform current density J=br. Here are the steps to arrive at the solution:
Step 1: Understand the Current Density
The current density J is given by:
J=br
where b is a constant and r is the radial distance from the center of the cylinder.
Step 2: Calculate the Differential Current Element
To find the total current flowing through a radius r1 (where r1<R), we consider a thin cylindrical shell of radius r and thickness dr. The area dA of this shell is:
dA=2πrdr
The differential current dI flowing through this area is:
dI=J⋅dA=(br)⋅(2πrdr)=2πbr2dr
Step 3: Integrate to Find the Total Current I
To find the total current I flowing through the area up to r1, we integrate dI from 0 to r1:
I=∫r10dI=∫r102πbr2dr
Calculating the integral:
I=2πb∫r10r2dr=2πb(r33)r10=2πbr313
Thus, the total current I is:
I=2πbr313
Step 4: Apply Ampère's Circuital Law
According to Ampère's law, the magnetic field B at a distance r1 from the center of the cylinder can be expressed as:
∮B⋅dl=μ0I
The left side of the equation simplifies to B⋅2πr1 (since B is constant along the circular path):
B⋅2πr1=μ0I
Substituting I:
B⋅2πr1=μ0(2πbr313)
Dividing both sides by 2πr1:
B=μ0br213
Step 5: Compare with Given Expression
The problem states that the magnetic field B at r1 is also given by:
B=μ0br21N
By comparing the two expressions for B:
μ0br213=μ0br21N
We can cancel μ0br21 (assuming r1≠0):
13=1N
Thus, we find:
N=3
Final Answer
The value of N is:
3
The current density J is given by:
J=br
where b is a constant and r is the radial distance from the center of the cylinder.
To find the total current flowing through a radius r1 (where r1<R), we consider a thin cylindrical shell of radius r and thickness dr. The area dA of this shell is:
dA=2πrdr
The differential current dI flowing through this area is:
dI=J⋅dA=(br)⋅(2πrdr)=2πbr2dr
To find the total current I flowing through the area up to r1, we integrate dI from 0 to r1:
I=∫r10dI=∫r102πbr2dr
Calculating the integral:
I=2πb∫r10r2dr=2πb(r33)r10=2πbr313
Thus, the total current I is:
I=2πbr313
According to Ampère's law, the magnetic field B at a distance r1 from the center of the cylinder can be expressed as:
∮B⋅dl=μ0I
The left side of the equation simplifies to B⋅2πr1 (since B is constant along the circular path):
B⋅2πr1=μ0I
Substituting I:
B⋅2πr1=μ0(2πbr313)
Dividing both sides by 2πr1:
B=μ0br213
The problem states that the magnetic field B at r1 is also given by:
B=μ0br21N
By comparing the two expressions for B:
μ0br213=μ0br21N
We can cancel μ0br21 (assuming r1≠0):
13=1N
Thus, we find:
N=3
The value of N is:
3
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3
18 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-1
5 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
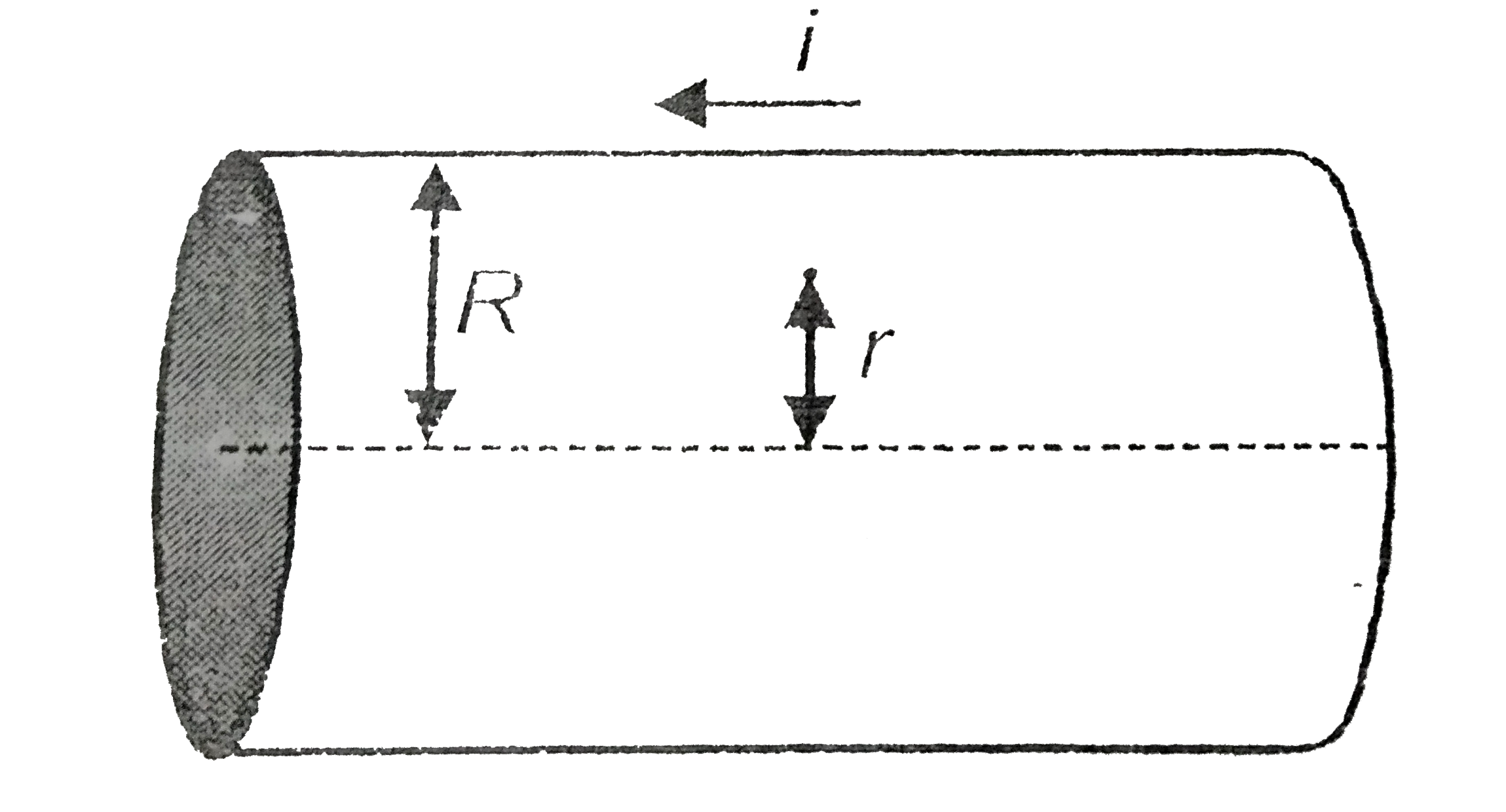
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
View SolutionA long thin walled pipe of radius R carries a current I along its length The current density is uniform over the circumference of the pipe The magnetic field at the center of the pipe due to quarter portion of the pipe shown, is
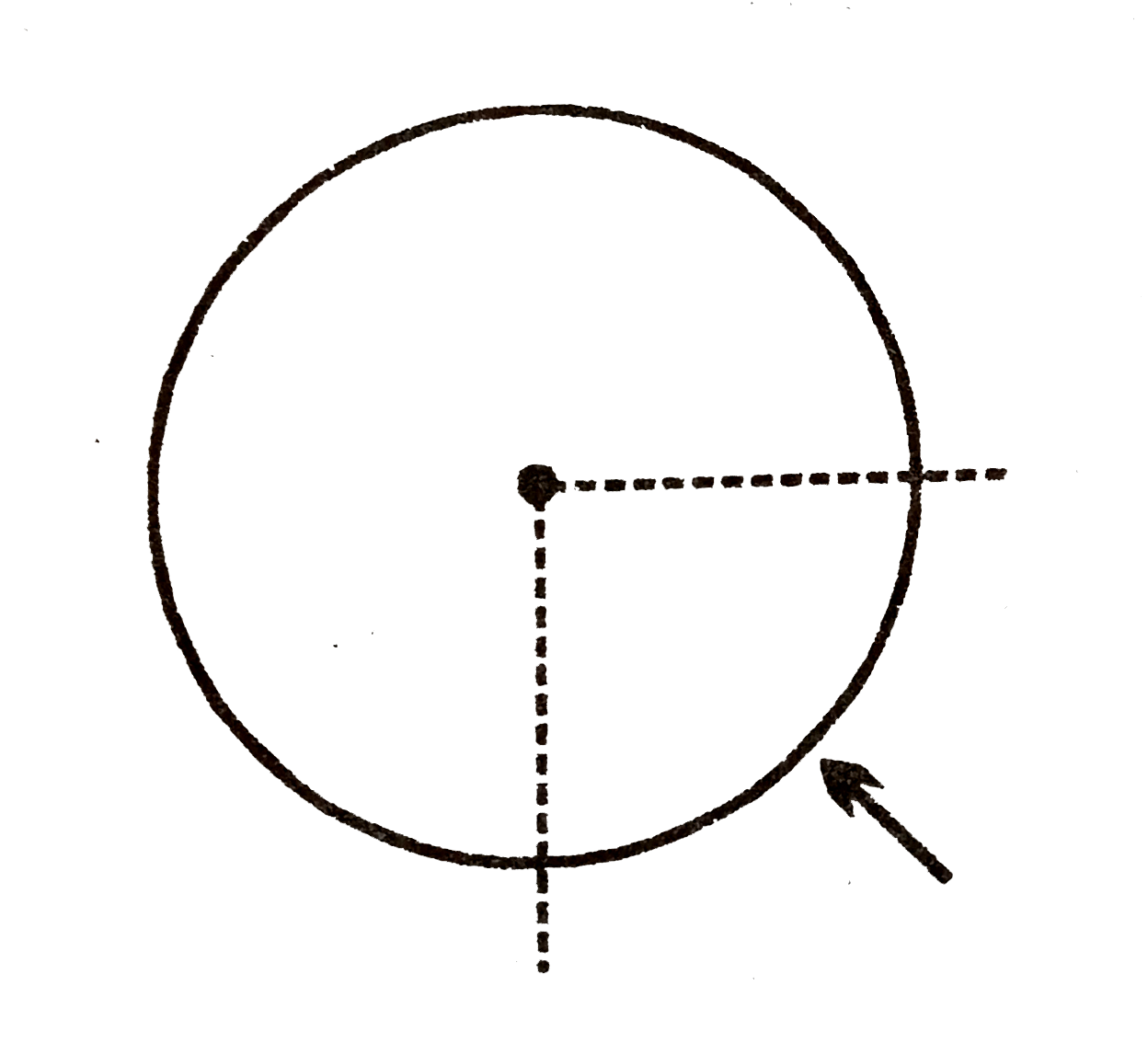 .
.
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View Solution
