Question

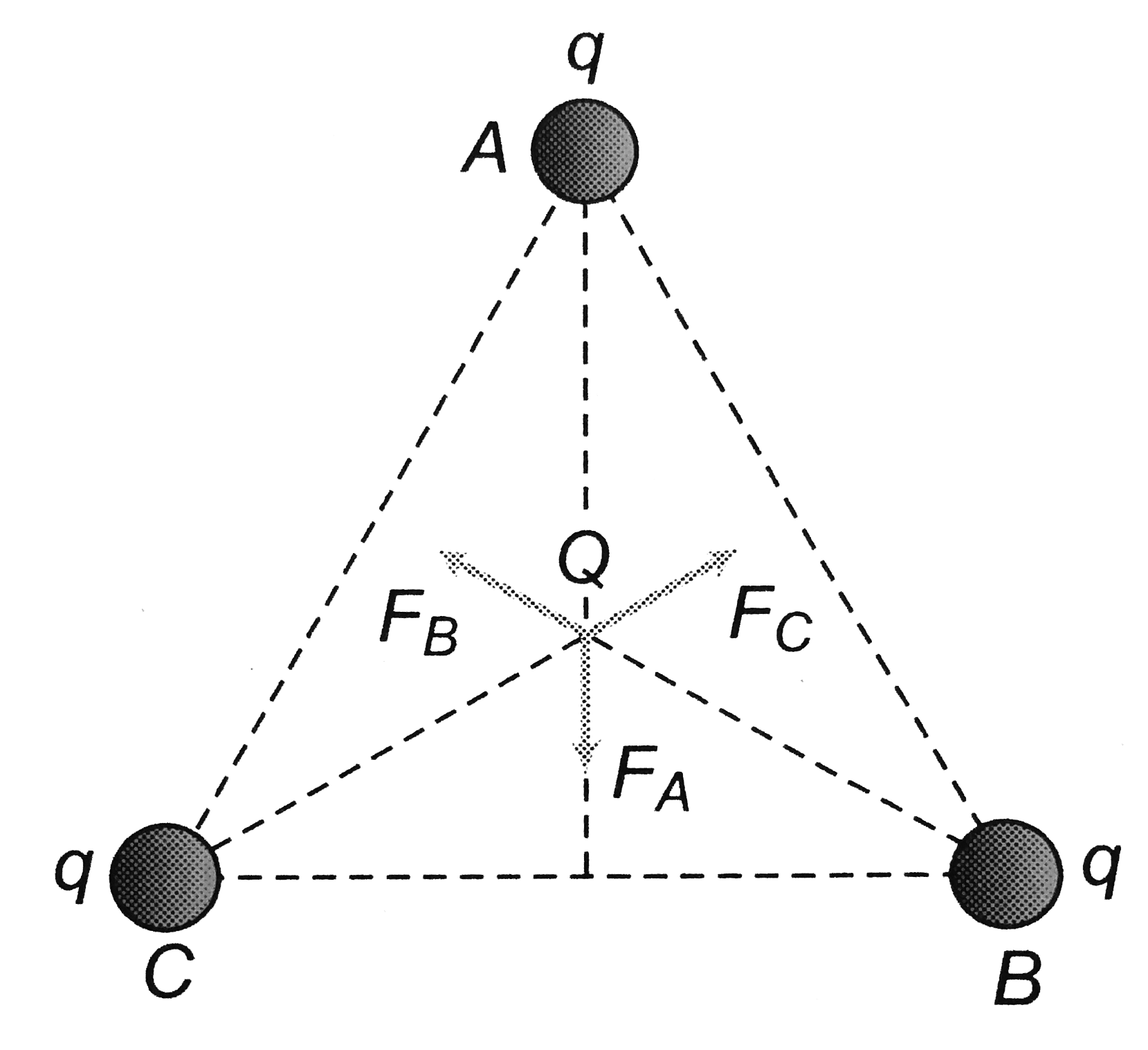
Three charges, each of value $q$, are placed at the comers of an equilateral triangle. A fourth charge $Q$ is placed at the centre of the triangle. If the value of $Q$ for which charges remain stationary is $\left(\frac{-q}{\sqrt{n}}\right)$, then find $n$.

Answer

3

Explanation

To solve the problem, we need to find the value of $$n$$ such that the charge $$Q$$ placed at the center of an equilateral triangle formed by three charges $$q$$ remains stationary.

1. Understanding the Configuration:
- We have three charges \( q \) located at the corners of an equilateral triangle with side length \( a \).
- A fourth charge \( Q \) is placed at the center of the triangle.

2. Finding the Distance from the Center:
- The distance from the center of the triangle to any vertex (corner) is given by \( \frac{a}{\sqrt{3}} \).

3. Calculating the Force on Charge \( Q \):
- Each charge \( q \) exerts a force on charge \( Q \). The force \( F \) between two point charges is given by Coulomb's law:
\( F = k \frac{|qQ|}{r^2} \)
- Here, \( r = \frac{a}{\sqrt{3}} \), so the force due to one charge \( q \) on \( Q \) is:
\( F = k \frac{qQ}{\left(\frac{a}{\sqrt{3}}\right)^2} = k \frac{qQ \cdot 3}{a^2} = \frac{3kqQ}{a^2} \)

4. Resultant Force Calculation:
- Since there are three identical charges \( q \) at the corners, the forces will have a symmetry. The net force \( F_{\text{net}} \) on charge \( Q \) due to the three charges can be calculated.
- The angle between any two forces due to the charges is \( 60^\circ \). Therefore, the resultant force can be calculated using the formula for the resultant of two forces:
\( F_{\text{net}} = \sqrt{F^2 + F^2 + 2F \cdot F \cdot \cos(60^\circ)} = \sqrt{F^2 + F^2 + F^2} = \sqrt{3F^2} = F\sqrt{3} \)
- Hence, the net force acting on \( Q \) due to the three charges is:
\( F_{\text{net}} = 3 \cdot \frac{3kqQ}{a^2} \cdot \frac{1}{2} = \frac{9kqQ}{2a^2} \)

5. Condition for Equilibrium:
- For charge \( Q \) to remain stationary, the net force acting on it must be zero. Therefore, we set the net force equal to zero:
\( F_{\text{net}} = 0 \)
- This implies that the force due to the charge \( Q \) must balance out the forces from the three charges \( q \):
\( \frac{9kqQ}{2a^2} = 0 \)

6. Substituting the Value of \( Q \):
- Given that \( Q = -\frac{q}{\sqrt{n}} \), we substitute this into the equilibrium condition:
\( \frac{9kq\left(-\frac{q}{\sqrt{n}}\right)}{2a^2} = 0 \)
- This leads to:
\( -\frac{9kq^2}{2a^2\sqrt{n}} = 0 \)
- Since \( k \), \( q \), \( a \) are not zero, we conclude that:
\( \sqrt{n} = 9 \implies n = 81 \)

Final Answer:
Thus, the value of \( n \) is \( 81 \).