A charged particle enters at point A and comes out from point B. Its velocity vector makes angle α and β with electric field at these two points, respectively. The ratio of kinetic energy of the charged particle at these two points (KδKA) will be (Given α=60∘ and β=30∘ ).
'(##CEN_KSR_PHY_JEE_C18_E01_014_Q05##)'
The correct Answer is:3
To find the ratio of kinetic energy of a charged particle at two points A and B when it enters and exits an electric field, we can follow these steps:
Step 1: Understand the relationship between velocity and kinetic energy
The kinetic energy K of a charged particle is given by the formula:
K=12mv2
where m is the mass of the particle and v is its velocity.
Step 2: Identify the components of velocity
At point A, the velocity VA makes an angle α with the electric field. The components of the velocity can be expressed as:
- Parallel component to the electric field: VA∥=VAcos(α)
- Perpendicular component to the electric field: VA⊥=VAsin(α)
At point B, the velocity VB makes an angle β with the electric field. The components of the velocity can be expressed as:
- Parallel component to the electric field: VB∥=VBcos(β)
- Perpendicular component to the electric field: VB⊥=VBsin(β)
Step 3: Apply the work-energy theorem
The work done by the electric field on the charged particle results in a change in kinetic energy. The change in kinetic energy can be related to the parallel component of the velocity, as only this component is affected by the electric field.
Step 4: Write the ratio of kinetic energies
The ratio of kinetic energies at points A and B can be expressed as:
KBKA=12mV2B12mV2A=V2BV2A
Step 5: Relate the velocities using the angles
Using the relationship between the components of the velocities and the angles:
VBVA=sin(β)sin(α)
Thus,
KBKA=(sin(β)sin(α))2
Step 6: Substitute the given angles
Given α=60∘ and β=30∘:
- sin(60∘)=√32
- sin(30∘)=12
Now substituting these values:
KBKA=⎛⎜⎝12√32⎞⎟⎠2=(1√3)2=13
Final Result
Thus, the ratio of kinetic energy at points B and A is:
KBKA=13
---
The kinetic energy K of a charged particle is given by the formula:
K=12mv2
where m is the mass of the particle and v is its velocity.
At point A, the velocity VA makes an angle α with the electric field. The components of the velocity can be expressed as:
- Parallel component to the electric field: VA∥=VAcos(α)
- Perpendicular component to the electric field: VA⊥=VAsin(α)
- Parallel component to the electric field: VB∥=VBcos(β)
- Perpendicular component to the electric field: VB⊥=VBsin(β)
The work done by the electric field on the charged particle results in a change in kinetic energy. The change in kinetic energy can be related to the parallel component of the velocity, as only this component is affected by the electric field.
The ratio of kinetic energies at points A and B can be expressed as:
KBKA=12mV2B12mV2A=V2BV2A
Using the relationship between the components of the velocities and the angles:
VBVA=sin(β)sin(α)
Thus,
KBKA=(sin(β)sin(α))2
Given α=60∘ and β=30∘:
- sin(60∘)=√32
- sin(30∘)=12
KBKA=⎛⎜⎝12√32⎞⎟⎠2=(1√3)2=13
Thus, the ratio of kinetic energy at points B and A is:
KBKA=13
Topper's Solved these Questions
Similar Questions
A charged particle enters at point A and comes out from point B. Its velocity vector makes angle α and β with electric field at these two points, respectively. The ratio of kinetic energy of the charged particle at these two points (KδKA) will be (Given α=60∘ and β=30∘ ).
'(##CEN_KSR_PHY_JEE_C18_E01_014_Q05##)'
View SolutionTwo particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles αandβ with horizontal. Find the time that elapses when their velocities are parallel.
View Solution
Knowledge Check
A charge particle is moving with a velocity 3ˆi+4ˆjm/sec and it has electric field E=10ˆkN/C at a given point. Find the magnitude of magneitc field at the same point due to the motion of the charge particle.
A100(μ0ɛ0)B25(μ0ɛ0)C12.5(μ0ɛ0)D50(μ0ɛ0)Two particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
A3(1−cos2α)=8sin2βBRange of A=maximum height of BCMaximum vlaue of β is 12sin−1(3)4DMaximum horizontal range of A =u2g and this occurs when β=12sin−1(3)8
A charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find
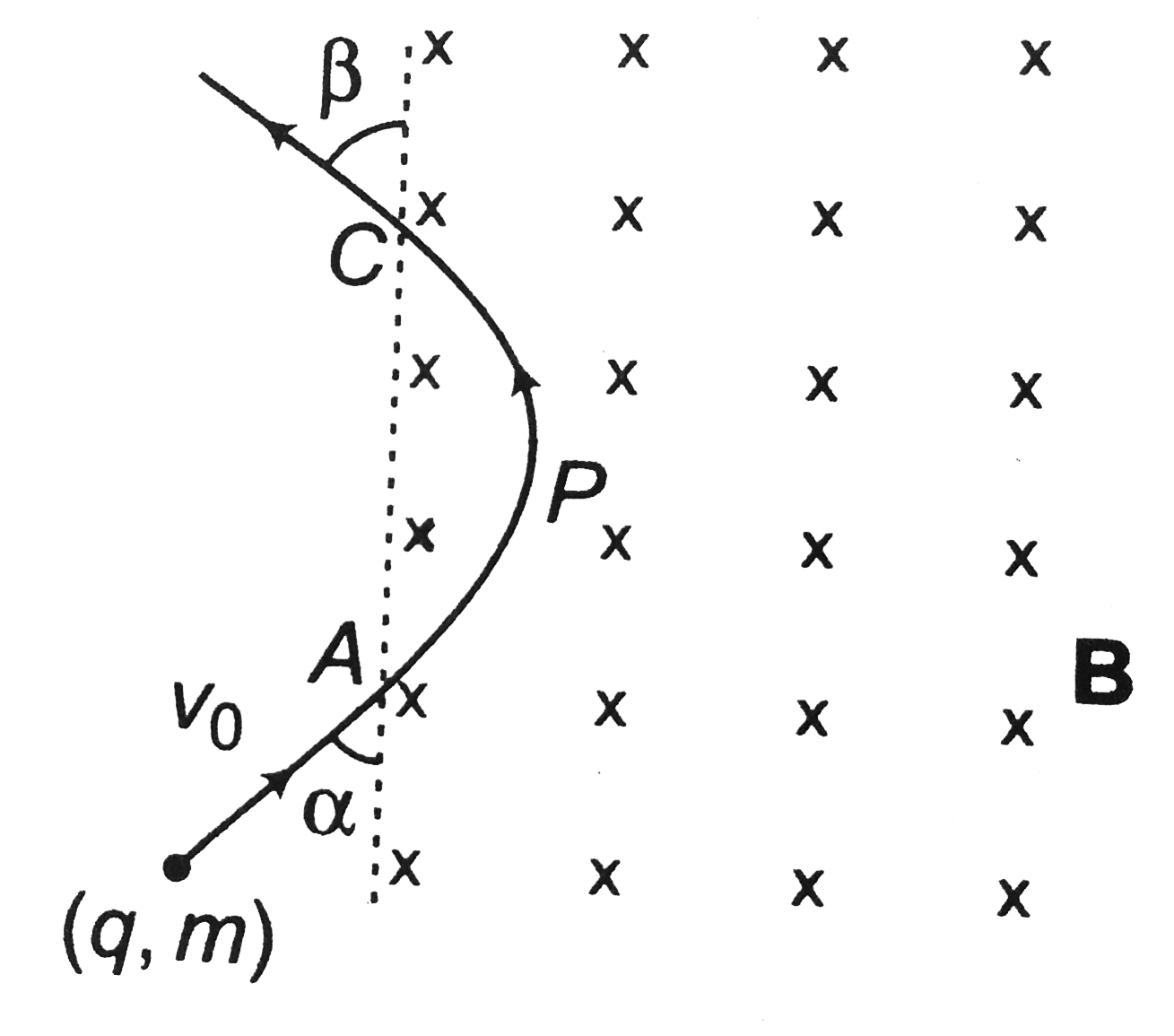
a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionTwo particles of masses m and 2m having same charges q each are placed in a uniform electric field E and allowed to move for the same time.If the ratio of their kinetic energies is ab then the value of a+b is _(--)
View SolutionFind the equivalent capacitance (in μF ) of the circuit between points A and B. (Given: C=5μF ).
'(##CEN_KSR_PHY_JEE_CO19_E01_018_Q08##)'
View SolutionA linear charge having linear charge density λ, penetrates a cube diagonally and that it penetrates a sphere diametrically as shown. The ratio of flux coming out of the cube and the sphere is √xy, Find (xy).
'(##CEN_KSR_PHY_JEE_C18_E01_011_Q03##)'
View SolutionAn electrostatic field line leaves at angle α from point charge +q1, and connects with point charge −q2 at angle β. Find the ratio q1/q2 (Given : α=60∘,β=90∘)
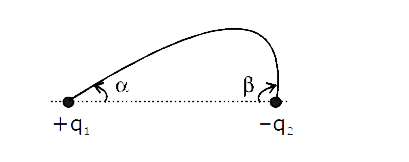
View SolutionA particle having charge q=+2.00μC and mess m=0.0100kg is connected to a string having length L=1.50 m and is tied to the pivot point P shown in the figure. The particle, string, and pivot point all lie op a frictionless horizontal table. The particle is released from rest when the string makes an angle θ=60∘ with a uniform electric field of magnitude E=300 V / m .The speed (in m / s ) of the particle when the string is parallel to the electric field (shown in figure) is x. Find 10x.
'(##CEN_KSR_PHY_JEE_C18_E01_021_Q09##)'
View Solution