Question

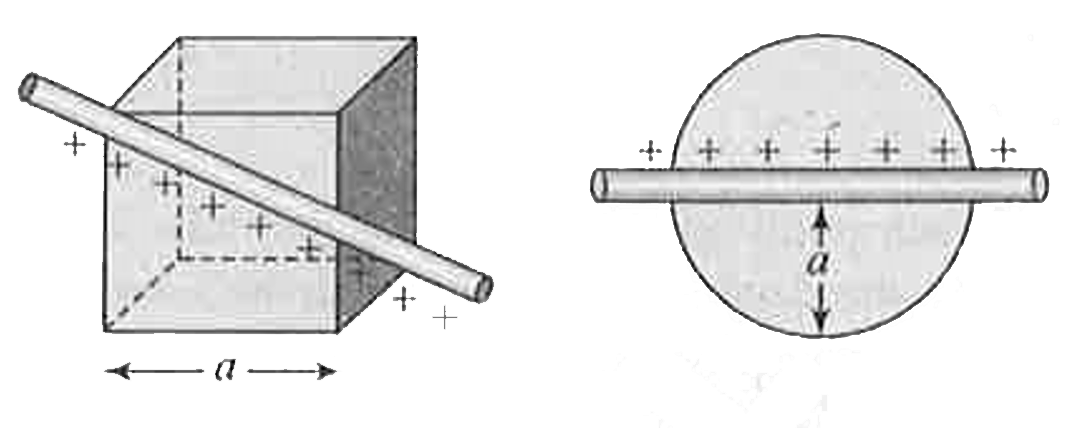
A linear charge having linear charge density $\lambda$, penetrates a cube diagonally and that it penetrates a sphere diametrically as shown. The ratio of flux coming out of the cube and the sphere is $\frac{\sqrt{x}}{y}$, Find $\left(xy\right)$.
'(##CEN_KSR_PHY_JEE_C18_E01_011_Q03##)'

Answer

6

Explanation

To find the ratio of the electric flux coming out of a cube and a sphere when a linear charge with linear charge density $$\lambda$$ penetrates both shapes, we can follow these steps:

Step 1: Understand the Geometry
- The linear charge penetrates the cube diagonally and the sphere diametrically.
- The length of the cube's diagonal can be represented as \( l \sqrt{3} \), where \( l \) is the side length of the cube.
- The diameter of the sphere is \( 2R \), where \( R \) is the radius of the sphere.

Step 2: Calculate the Charge Enclosed
- For the cube:
- The charge enclosed by the cube is given by:
\( Q_c = \lambda \cdot l \sqrt{3} \)
- For the sphere:
- The charge enclosed by the sphere is given by:
\( Q_s = \lambda \cdot 2R \)

Step 3: Apply Gauss's Law
- According to Gauss's Law, the electric flux \( \Phi \) through a closed surface is given by:
\( \Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0} \)
- For the cube, the electric flux \( \Phi_c \) is:
\( \Phi_c = \frac{Q_c}{\epsilon_0} = \frac{\lambda l \sqrt{3}}{\epsilon_0} \)
- For the sphere, the electric flux \( \Phi_s \) is:
\( \Phi_s = \frac{Q_s}{\epsilon_0} = \frac{\lambda \cdot 2R}{\epsilon_0} \)

Step 4: Find the Ratio of Fluxes
- The ratio of the electric fluxes is:
\( \frac{\Phi_c}{\Phi_s} = \frac{\frac{\lambda l \sqrt{3}}{\epsilon_0}}{\frac{\lambda \cdot 2R}{\epsilon_0}} = \frac{l \sqrt{3}}{2R} \)

Step 5: Substitute Values
- If we assume \( l = R \) (the side of the cube is equal to the radius of the sphere), then:
\( \frac{\Phi_c}{\Phi_s} = \frac{R \sqrt{3}}{2R} = \frac{\sqrt{3}}{2} \)

Step 6: Identify \( x \) and \( y \)
- From the ratio \( \frac{\Phi_c}{\Phi_s} = \frac{\sqrt{3}}{2} \), we can identify \( x = 3 \) and \( y = 2 \).

Step 7: Calculate \( xy \)
- Therefore, \( xy = 3 \cdot 2 = 6 \).

Final Answer
The value of \( xy \) is \( 6 \).

---