Three equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
kq/r2
3kq/r2
√3kq/r2
zero
The correct Answer is:D
To find the electric field intensity at the centroid of an equilateral triangle with three equal charges placed at its corners, we can follow these steps:
1. Understanding the Configuration:
We have three equal charges, each of magnitude +q, placed at the vertices of an equilateral triangle. Let's denote the vertices as A, B, and C.
2. Identifying the Centroid:
The centroid (G) of an equilateral triangle is the point where the three medians intersect. It is also the center of symmetry for the triangle.
3. Calculating the Electric Field due to One Charge:
The electric field →E due to a point charge +q at a distance r is given by the formula:
→E=k⋅qr2
where k is Coulomb's constant.
4. Distance from Vertices to Centroid:
In an equilateral triangle, the distance from each vertex to the centroid is 23 of the height of the triangle. If the side length of the triangle is a, the height h can be calculated as:
h=√32a
Therefore, the distance r from each vertex to the centroid is:
r=23h=23⋅√32a=√33a
5. Direction of Electric Fields:
The electric field vectors due to each charge will point away from the charges since they are positive. The angles between the electric fields at the centroid due to each charge will be 120∘.
6. Vector Addition of Electric Fields:
When we add the electric fields vectorially, we can use the symmetry of the triangle. The electric fields due to the three charges will have equal magnitudes and will be separated by 120∘.
7. Net Electric Field Calculation:
The symmetry of the arrangement means that the components of the electric fields in the horizontal direction will cancel out. Similarly, the vertical components will also cancel out. Therefore, the net electric field →Enet at the centroid is:
→Enet=→EA+→EB+→EC=0
Conclusion:
The net electric field intensity at the centroid of the triangle is zero.
We have three equal charges, each of magnitude +q, placed at the vertices of an equilateral triangle. Let's denote the vertices as A, B, and C.
The centroid (G) of an equilateral triangle is the point where the three medians intersect. It is also the center of symmetry for the triangle.
The electric field →E due to a point charge +q at a distance r is given by the formula:
→E=k⋅qr2
where k is Coulomb's constant.
In an equilateral triangle, the distance from each vertex to the centroid is 23 of the height of the triangle. If the side length of the triangle is a, the height h can be calculated as:
h=√32a
Therefore, the distance r from each vertex to the centroid is:
r=23h=23⋅√32a=√33a
The electric field vectors due to each charge will point away from the charges since they are positive. The angles between the electric fields at the centroid due to each charge will be 120∘.
When we add the electric fields vectorially, we can use the symmetry of the triangle. The electric fields due to the three charges will have equal magnitudes and will be separated by 120∘.
The symmetry of the arrangement means that the components of the electric fields in the horizontal direction will cancel out. Similarly, the vertical components will also cancel out. Therefore, the net electric field →Enet at the centroid is:
→Enet=→EA+→EB+→EC=0
The net electric field intensity at the centroid of the triangle is zero.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Comprehension
Explore 25 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Five equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionThree charges, each of value q, are placed at the vartices of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. (i) If Q=−q, will the charge at the vertices move towards the centre of fly away from it? (ii) For what value of Q will the charges remain stationary?
View Solution
Knowledge Check
Three charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If Q=−q:
Athe charges will move towards the centreBthe charges will move away from the centreCthe charges will remain stationaryDthe charges may move in any directionThree charges each of magnitude q are placed at the corners of an equilateral triangle, the electrostatic force on the charge place at the centre is (each side of triangle is L)
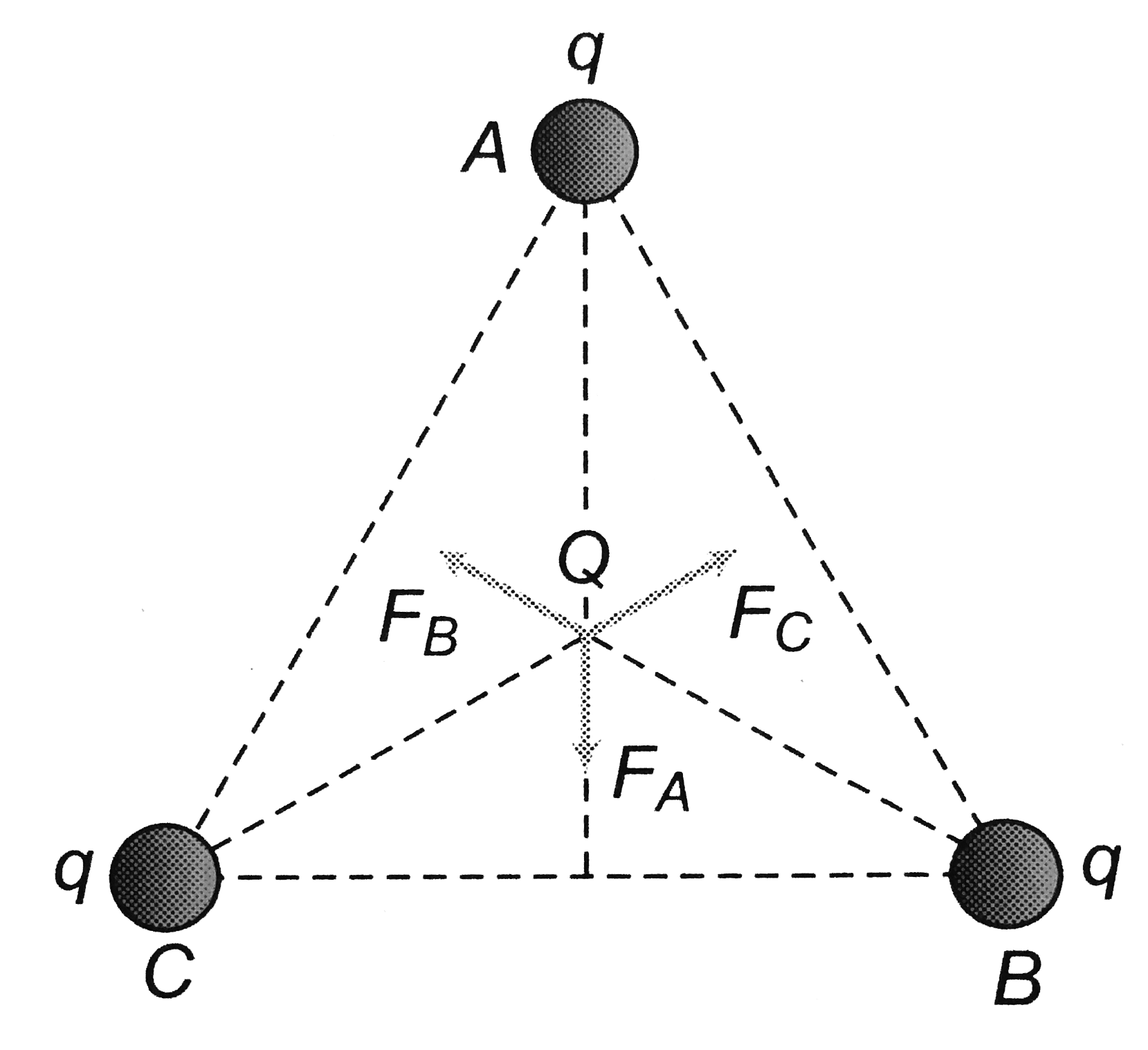 AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2
AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2At each corner of an equilateral triangle identical charges are placed. Then at the centre of the triangle
Athe resultant electric intensity is zeroBthe net potential is zeroCboth electric intensity and potential are zeroDneither electric intensity nor potential are zero
Three charges, each of value q, are placed at the comers of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If the value of Q for which charges remain stationary is (−q√n), then find n.
View SolutionThree charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the center of the triangle.
a. Find the net force on charge q.
b. If Q=−q, will the charges at the corners move toward the center or fly away from it ?
c. For what value of Q and O will the charges remain stationary ?
d. In situation (c), how much work is done in removing the charges to infinity ?
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
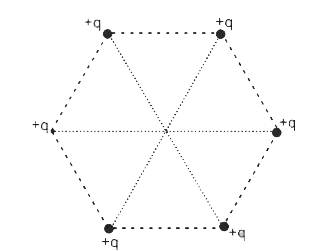
View SolutionTwo charged particles of charges +0.1 μC and -0.1 μC are kept on the vertices of an equilateral triangle of side 10 cm. Calculate the electric field intensity at the centroid of the triangle.
View SolutionAssertion: Three equal charges are situated on a circle of radius r such that they form on equilateral triangle, then the electric field intensity at the centre is zero.
Reason: The force on unit positive charge at the centre, due to the three equal charges are represented by three sides of a triangle taken in the same order. Therefore, electric field intensity at centre is zero.
View Solution

