The motion of a particle of mass m is given by x=0 for t<0s,x(t)=Asin4πt for 0<t<(14)s
(A>0) and x=0 for t>(14)s.
The force at t=(18)s on the particle is −16π2A−m
The particle is acted upon by on impulse of magnitude 4π2A−m at t=0s and t=(14)s
The particle is not acted upon by any force
The particle is not acted upon by a constant force
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the motion of the particle given by the equations provided.
Step 1: Understand the motion of the particle
The motion of the particle is defined in three intervals:
1. For t<0: x=0
2. For 0<t<14: x(t)=Asin(4πt) (where A>0)
3. For t>14: x=0
Step 2: Find the velocity of the particle
To find the velocity v(t), we differentiate the position function x(t) with respect to time t:
v(t)=dxdt=ddt(Asin(4πt))=4πAcos(4πt)
Step 3: Find the acceleration of the particle
Next, we differentiate the velocity function v(t) to find the acceleration a(t):
a(t)=dvdt=ddt(4πAcos(4πt))=−16π2Asin(4πt)
Step 4: Evaluate acceleration at t=18 seconds
Now, we will evaluate the acceleration at t=18 seconds:
a(18)=−16π2Asin(4π⋅18)=−16π2Asin(π2)=−16π2A
Step 5: Calculate the force acting on the particle
Using Newton's second law, we can find the force F acting on the particle:
F=m⋅a=m⋅(−16π2A)=−16π2mA
Step 6: Analyze the options
Now we can analyze the options given in the problem based on our calculations:
- Option A: The force at t=18 seconds is −16π2mA (Correct)
- Option B: The impulse at t=0 and t=14 is the same (Correct, since the impulse depends on the change in momentum)
- Option C: The particle is acted upon by a constant force (Incorrect, since the force changes with time)
- Option D: The particle is not acted upon by any constant force (Correct)
Conclusion
The correct options are A, B, and D.
The motion of the particle is defined in three intervals:
1. For t<0: x=0
2. For 0<t<14: x(t)=Asin(4πt) (where A>0)
3. For t>14: x=0
To find the velocity v(t), we differentiate the position function x(t) with respect to time t:
v(t)=dxdt=ddt(Asin(4πt))=4πAcos(4πt)
Next, we differentiate the velocity function v(t) to find the acceleration a(t):
a(t)=dvdt=ddt(4πAcos(4πt))=−16π2Asin(4πt)
Now, we will evaluate the acceleration at t=18 seconds:
a(18)=−16π2Asin(4π⋅18)=−16π2Asin(π2)=−16π2A
Using Newton's second law, we can find the force F acting on the particle:
F=m⋅a=m⋅(−16π2A)=−16π2mA
Now we can analyze the options given in the problem based on our calculations:
- Option A: The force at t=18 seconds is −16π2mA (Correct)
- Option B: The impulse at t=0 and t=14 is the same (Correct, since the impulse depends on the change in momentum)
- Option C: The particle is acted upon by a constant force (Incorrect, since the force changes with time)
- Option D: The particle is not acted upon by any constant force (Correct)
The correct options are A, B, and D.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Multiple correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
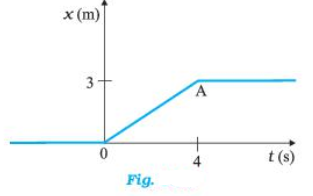
Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
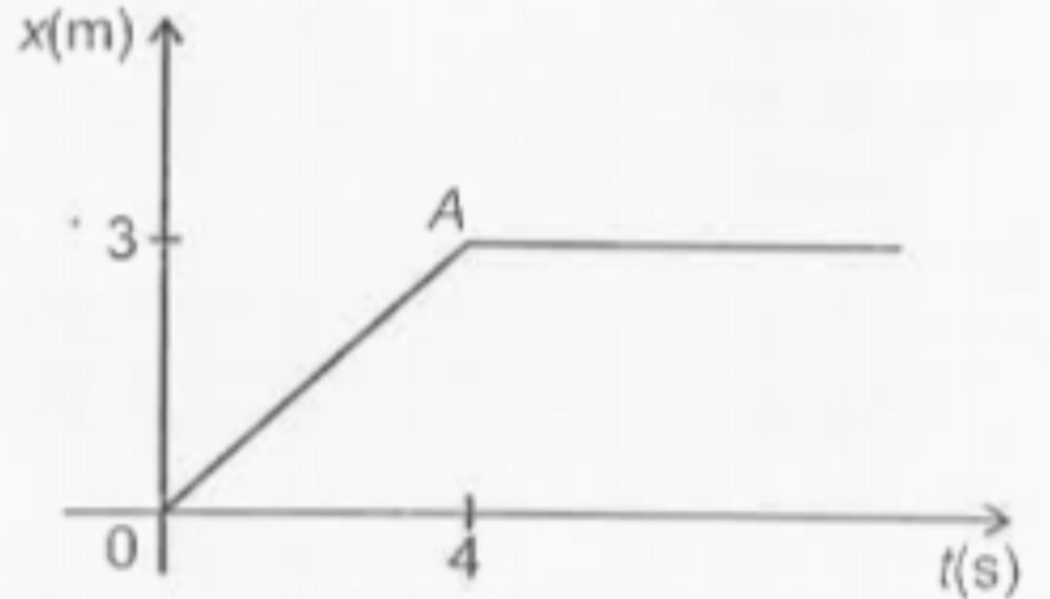
View SolutionThe figure shows the position time graph of a particle of mass 40 kg. What is the force acting on the particle of 0<t<4 s
View Solution
Knowledge Check
Figure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
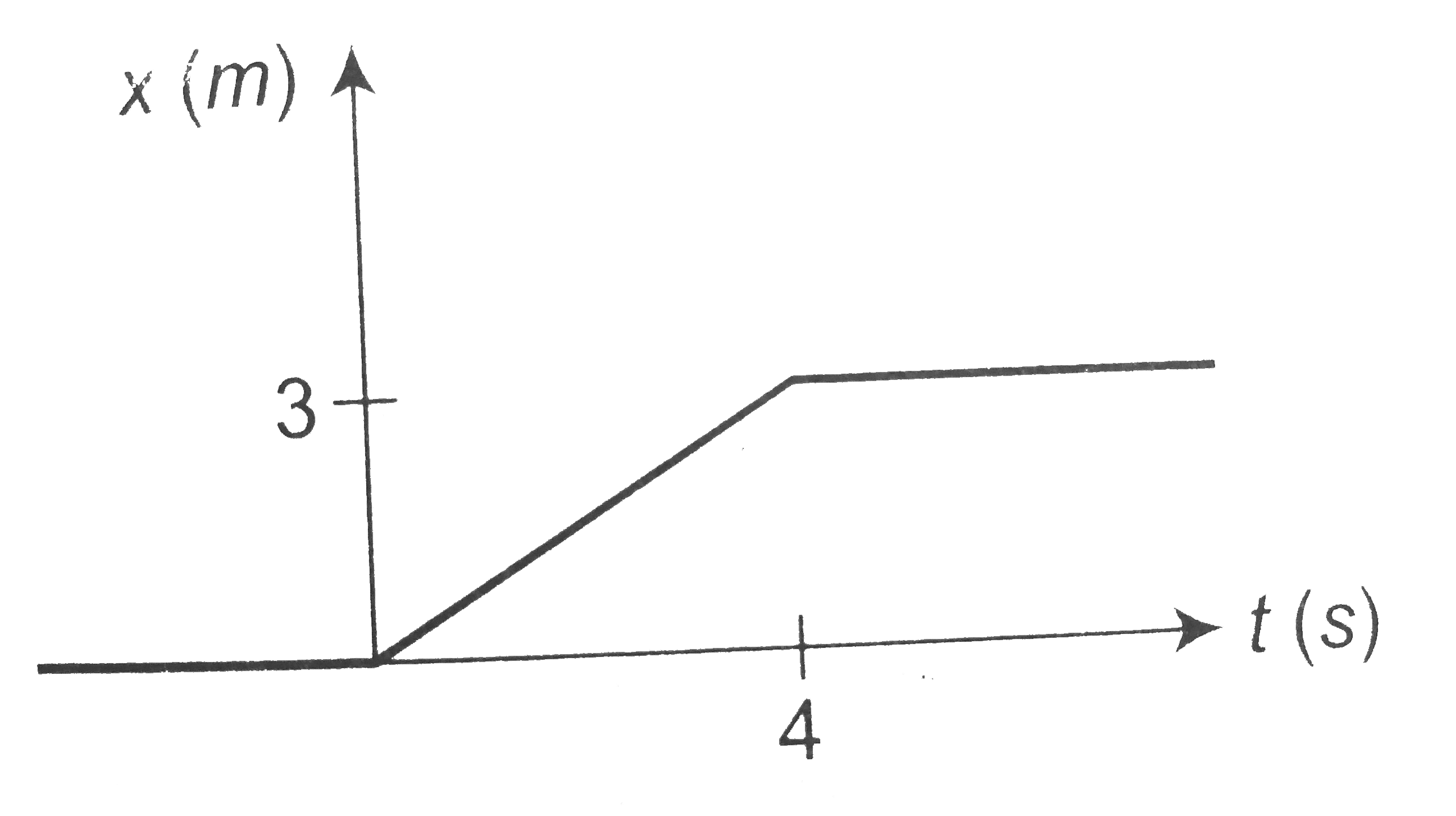 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
The equation of a wave on a string of linear mass density 0.04kgm−1 is given by
y=0.02(m)sin[2π(t0.04(s)−x0.50(m))].
Then tension in the string is
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionThe acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
View SolutionThe body moves along the x−axis . At time t=0 the velocity of particle is +0.5m/s. The acceleration of particle in different time interval is given as:
a=⎧⎪ ⎪⎨⎪ ⎪⎩−1m/s2 0s≤t≤3s−2m/s2 3s<t<6s+4m/s2 6s≤t≤10s
View SolutionThe position of a particle moving on X-axis is given by
x=At3+Bt2+Ct+D.
The numerical values of A,B,C,D are 1,4,-2 and 5 respectively and I units are used. Find a. the dimensions of A,B, C and D b. the velocity of the particle at t=4s, the acceleration of he particle at t=4s, d. The average velocity during the interval t=0 to t=4s, the average accelerationduring the interval t=0 to t=4s.
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionAcceleration of a particle is given by
a=1/V
Where V is the velocity . Find
(i) Velocity of particle at time t, given that v = 10 m/s at t = 0.
(ii) Velocity of particle when its position is x, given that speed is 3 m/s at x = 0.
View Solution