Velocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
12m
16m
4m
8m
The correct Answer is:B
To solve the problem, we need to calculate the distance traveled by the particle in the time interval from t=0 to t=4 seconds using the given velocity equations.
Step 1: Identify the time intervals and corresponding velocity equations
The velocity equations are:
- For t≤2 seconds: v=2t−4
- For t>2 seconds: v=4−2t
Step 2: Calculate the distance from t=0 to t=2 seconds
We will integrate the velocity function from t=0 to t=2:
Distance1=∫20(2t−4)dt
Calculating the integral:
∫(2t−4)dt=t2−4t
Now, evaluate it from 0 to 2:
Distance1=(t2−4t)20=(22−4⋅2)−(02−4⋅0)=(4−8)−0=−4
Since distance cannot be negative, we take the absolute value:
Distance1=|−4|=4 meters
Step 3: Calculate the distance from t=2 to t=4 seconds
Now we will integrate the velocity function from t=2 to t=4:
Distance2=∫42(4−2t)dt
Calculating the integral:
∫(4−2t)dt=4t−t2
Now, evaluate it from 2 to 4:
Distance2=(4t−t2)42=(4⋅4−42)−(4⋅2−22)=(16−16)−(8−4)=0−4=−4
Again, taking the absolute value:
Distance2=|−4|=4 meters
Step 4: Calculate the total distance traveled
Now, we add the distances from both intervals:
Total Distance=Distance1+Distance2=4+4=8 meters
Final Answer
The distance traveled by the particle from t=0 to t=4 seconds is 8 meters.
---
The velocity equations are:
- For t≤2 seconds: v=2t−4
- For t>2 seconds: v=4−2t
We will integrate the velocity function from t=0 to t=2:
Distance1=∫20(2t−4)dt
∫(2t−4)dt=t2−4t
Now, evaluate it from 0 to 2:
Distance1=(t2−4t)20=(22−4⋅2)−(02−4⋅0)=(4−8)−0=−4
Since distance cannot be negative, we take the absolute value:
Distance1=|−4|=4 meters
Now we will integrate the velocity function from t=2 to t=4:
Distance2=∫42(4−2t)dt
∫(4−2t)dt=4t−t2
Now, evaluate it from 2 to 4:
Distance2=(4t−t2)42=(4⋅4−42)−(4⋅2−22)=(16−16)−(8−4)=0−4=−4
Again, taking the absolute value:
Distance2=|−4|=4 meters
Now, we add the distances from both intervals:
Total Distance=Distance1+Distance2=4+4=8 meters
The distance traveled by the particle from t=0 to t=4 seconds is 8 meters.
Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:MCQ_TYPE
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
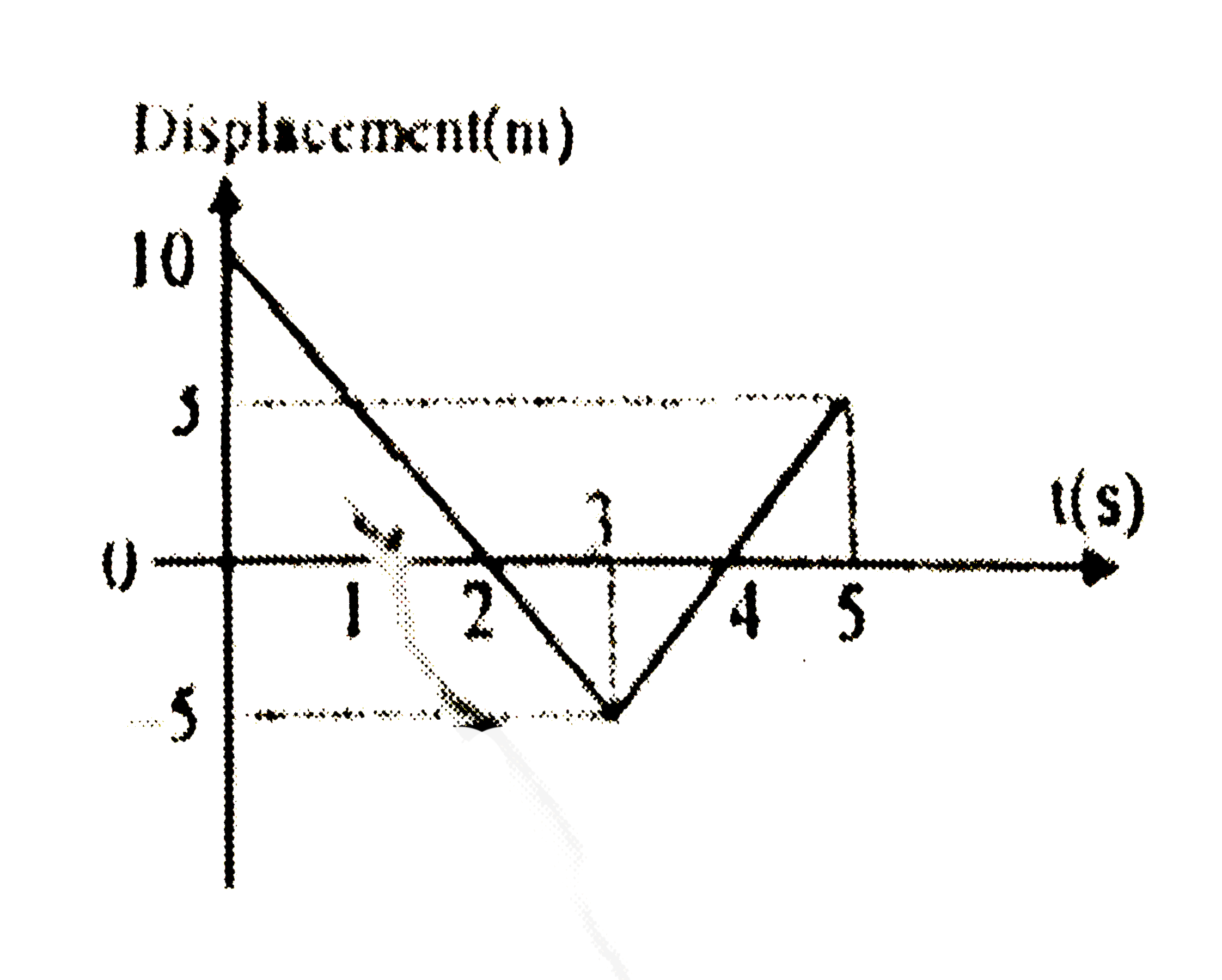
The diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is
View SolutionDisplacement-time graph of a particle moving in a straight line is as shown in figure. Mass of the particle is 2 kg. The total impulse imparted to the particle in a time interval from t=0 to t=6 s in N-s will be

View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
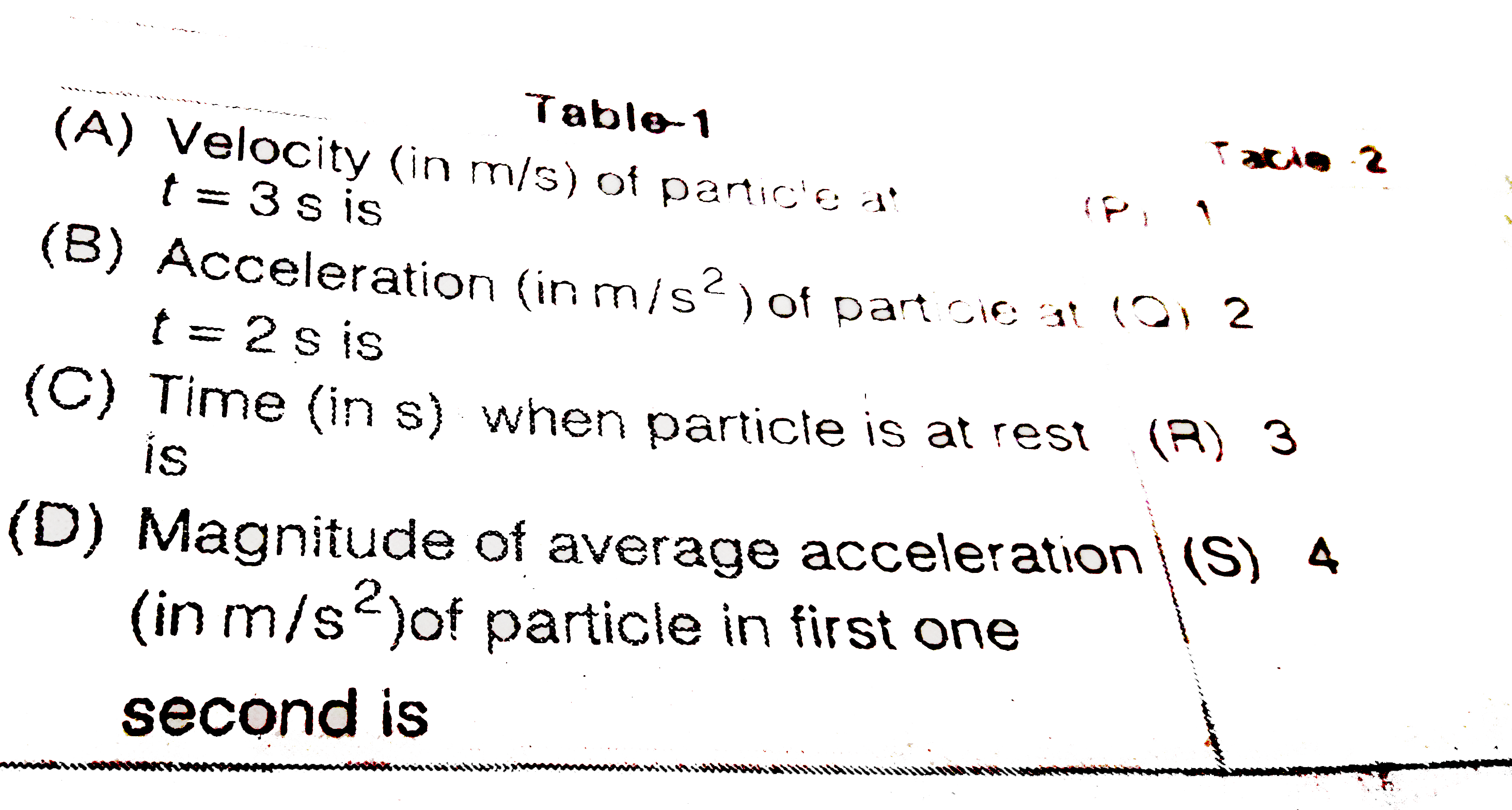
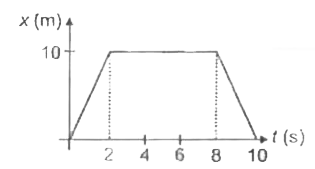
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
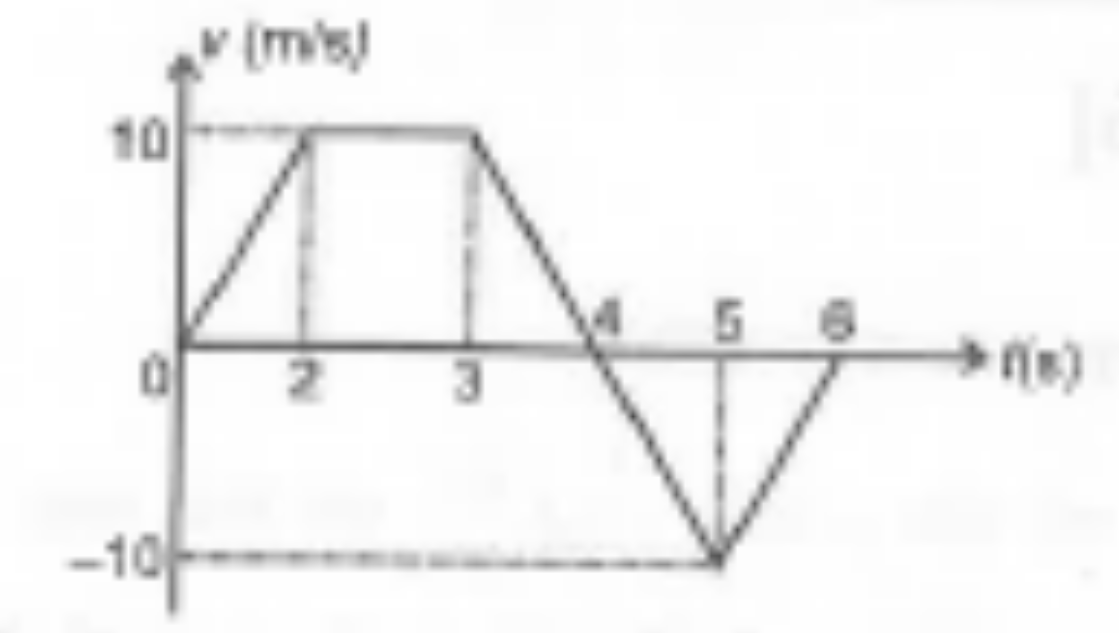
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is

View SolutionA particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution

