The speed of a body moving on a straight trach varies according to v=45t2+3 for 0<t<5 sec and v=3t+8 for t>5 sec. If dinstances are in meters, find the distance moved by a particle at the end of 10 sec.
The correct Answer is:(1453+3052)m
To solve the problem of finding the distance moved by a particle at the end of 10 seconds, we will break the process down into steps.
1. Identify the velocity functions:
- For 0<t<5 seconds:
v=45t2+3
- For t≥5 seconds:
v=3t+8
2. Calculate the distance for the first interval (0 to 5 seconds):
- The distance x1 can be found by integrating the velocity function from t=0 to t=5:
x1=∫50vdt=∫50(45t2+3)dt
3. Perform the integration:
- The integral can be split:
x1=∫5045t2dt+∫503dt
- Calculate each part:
- For ∫5045t2dt:
=45⋅(t33)50=45⋅1253=1003
- For ∫503dt:
=3(t)50=3⋅5=15
- Combine the results:
x1=1003+15=1003+453=1453 meters
4. Calculate the distance for the second interval (5 to 10 seconds):
- The distance x2 can be found by integrating the second velocity function from t=5 to t=10:
x2=∫105(3t+8)dt
5. Perform the integration:
- Calculate the integral:
x2=∫105(3t+8)dt=(3t22+8t)105
- Evaluate at the limits:
- For t=10:
=3(102)2+8(10)=3002+80=150+80=230
- For t=5:
=3(52)2+8(5)=752+40=37.5+40=77.5
- Combine the results:
x2=230−77.5=152.5 meters
6. Total distance moved in 10 seconds:
- Combine the distances from both intervals:
xtotal=x1+x2=1453+152.5
- Convert 152.5 to a fraction:
152.5=3052
- Find a common denominator (6):
xtotal=1453+9156=2906+9156=12056≈200.83 meters
Final Answer:
The total distance moved by the particle at the end of 10 seconds is approximately 200.83 meters.
- For 0<t<5 seconds:
v=45t2+3
- For t≥5 seconds:
v=3t+8
- The distance x1 can be found by integrating the velocity function from t=0 to t=5:
x1=∫50vdt=∫50(45t2+3)dt
- The integral can be split:
x1=∫5045t2dt+∫503dt
- Calculate each part:
- For ∫5045t2dt:
=45⋅(t33)50=45⋅1253=1003
- For ∫503dt:
=3(t)50=3⋅5=15
- Combine the results:
x1=1003+15=1003+453=1453 meters
- The distance x2 can be found by integrating the second velocity function from t=5 to t=10:
x2=∫105(3t+8)dt
- Calculate the integral:
x2=∫105(3t+8)dt=(3t22+8t)105
- Evaluate at the limits:
- For t=10:
=3(102)2+8(10)=3002+80=150+80=230
- For t=5:
=3(52)2+8(5)=752+40=37.5+40=77.5
- Combine the results:
x2=230−77.5=152.5 meters
- Combine the distances from both intervals:
xtotal=x1+x2=1453+152.5
- Convert 152.5 to a fraction:
152.5=3052
- Find a common denominator (6):
xtotal=1453+9156=2906+9156=12056≈200.83 meters
The total distance moved by the particle at the end of 10 seconds is approximately 200.83 meters.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Single Correct Answer type
Explore 491 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
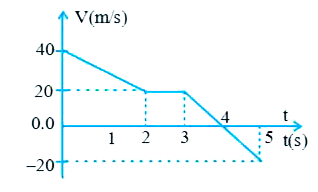
In the given v-t graph, the distance travelled by the body in 5 sec will be :
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Acceleration of particle at the end of 3rd second of motion is :
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionA particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
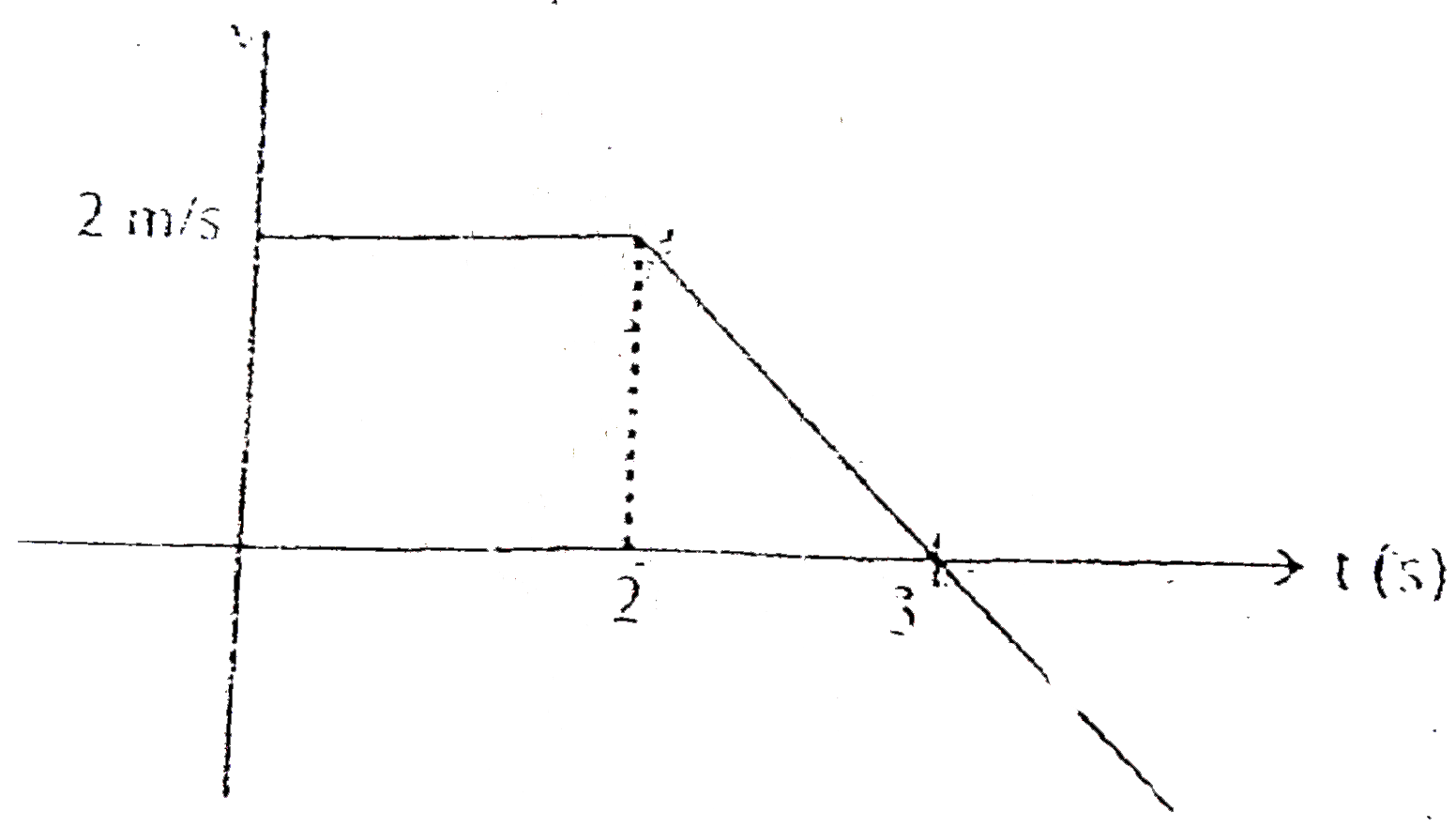
View SolutionA particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
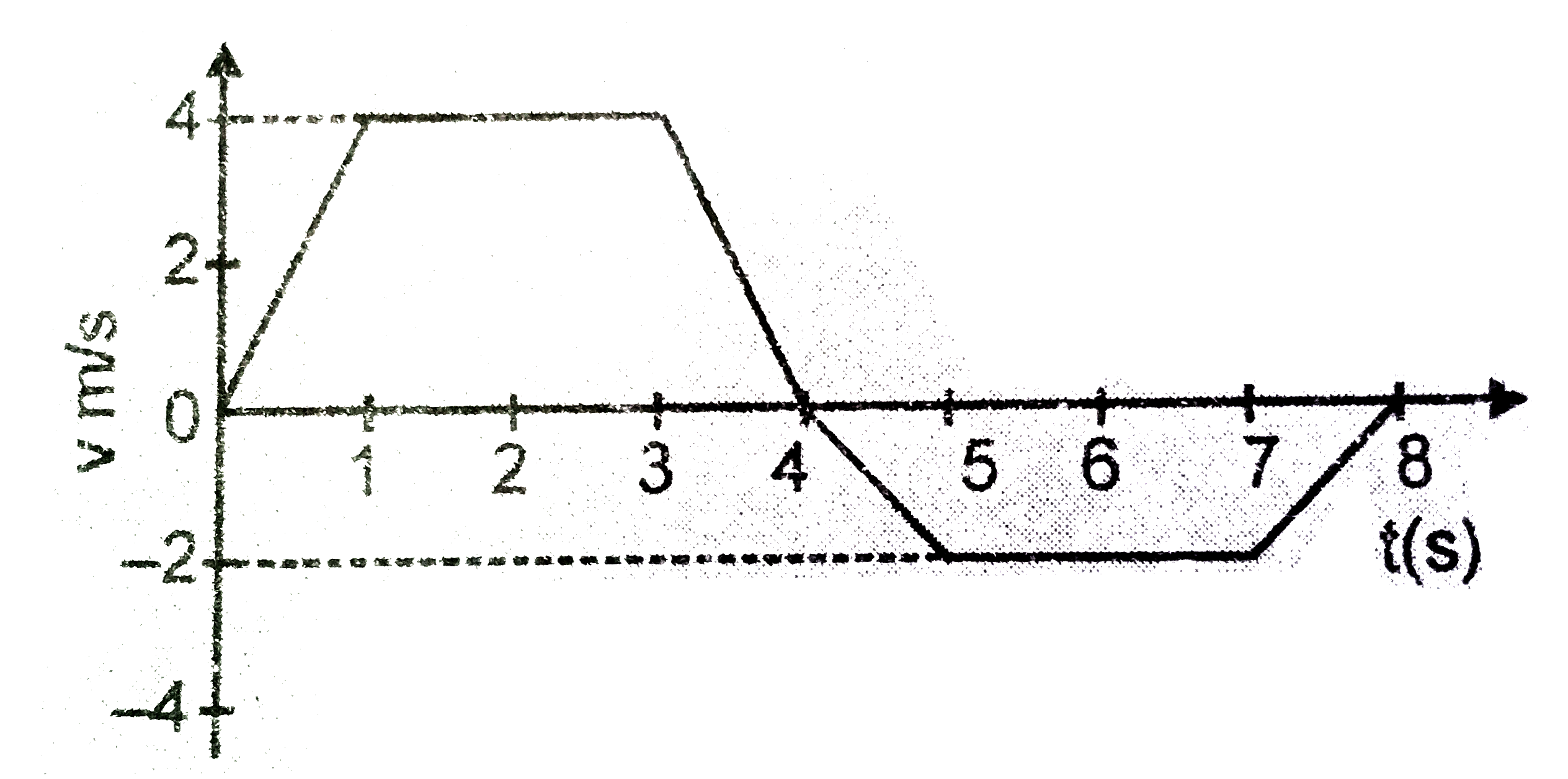
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
View SolutionVelocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View Solution