A man of mass m is standing on a lift which moves down with an upward acceleration a. Find the pseudo force acting on the man as observed by himself. Find the pseudo force acting on the man if the lift falls freely.
To solve the problem, we will analyze the two scenarios separately: when the lift moves down with an upward acceleration a and when the lift falls freely.
Step 1: Pseudo Force when the Lift Moves Down with Upward Acceleration a
1. Understanding the Situation: The man is in a lift that is moving downward but accelerating upward with an acceleration a.
2. Identifying the Pseudo Force: In a non-inertial frame (the frame of the man in the lift), a pseudo force acts on the man. This pseudo force acts in the opposite direction to the acceleration of the lift.
3. Direction of the Pseudo Force: Since the lift is accelerating upward, the pseudo force will act downward.
4. Calculating the Pseudo Force: The magnitude of the pseudo force Fpseudo can be calculated using the formula:
Fpseudo=m⋅a
where m is the mass of the man and a is the upward acceleration of the lift.
Step 2: Pseudo Force when the Lift Falls Freely
1. Understanding the Situation: In this case, the lift is in free fall, meaning it is accelerating downward with an acceleration equal to the acceleration due to gravity g.
2. Identifying the Pseudo Force: Again, in the non-inertial frame of the man, a pseudo force acts on him. This time, since the lift is accelerating downward, the pseudo force will act upward.
3. Direction of the Pseudo Force: The pseudo force acts in the opposite direction of the lift's acceleration, which is upward.
4. Calculating the Pseudo Force: The magnitude of the pseudo force when the lift is in free fall is given by:
Fpseudo=m⋅g
where g is the acceleration due to gravity.
Final Summary
- When the lift moves down with an upward acceleration a:
- Pseudo Force Fpseudo=m⋅a (acting downward)
- When the lift falls freely:
- Pseudo Force Fpseudo=m⋅g (acting upward)
2. Identifying the Pseudo Force: In a non-inertial frame (the frame of the man in the lift), a pseudo force acts on the man. This pseudo force acts in the opposite direction to the acceleration of the lift.
3. Direction of the Pseudo Force: Since the lift is accelerating upward, the pseudo force will act downward.
4. Calculating the Pseudo Force: The magnitude of the pseudo force Fpseudo can be calculated using the formula:
Fpseudo=m⋅a
where m is the mass of the man and a is the upward acceleration of the lift.
2. Identifying the Pseudo Force: Again, in the non-inertial frame of the man, a pseudo force acts on him. This time, since the lift is accelerating downward, the pseudo force will act upward.
3. Direction of the Pseudo Force: The pseudo force acts in the opposite direction of the lift's acceleration, which is upward.
4. Calculating the Pseudo Force: The magnitude of the pseudo force when the lift is in free fall is given by:
Fpseudo=m⋅g
where g is the acceleration due to gravity.
- Pseudo Force Fpseudo=m⋅a (acting downward)
- When the lift falls freely:
- Pseudo Force Fpseudo=m⋅g (acting upward)
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type
491 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
A man of mass m is standing in an elevator moving downward with an acceleration g4. The force exerted by the bottom surface of the elevator on the man will be
View SolutionA man of mass 70 kg stands on a weighing scale in a lift which is moving downward with the uniform acceleration of 5ms2 . The reading on the weighing scale is
View SolutionA man of mass M stands on a weighing machine in an elevator accelerating upwards with an acceleration a. Draw the free-body diagram of the man as observed by the observer A (stationary on the ground) and observer B (stationary on the elevator). Also, calculate the reading of the weighing machine.

View SolutionA person of mass m is on the floor of a lift. The lift is moving down with an acceleration 'a'. Then :
a) the net force is acting in downward direction and is equal to mg
b) the force mg must be greater than reaction force
c) the man appears to be lighter than his true weight by a factor (a/g)
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View SolutionA man of mass m is on the floor of a lift. The lift moving up with acceleration 'a', then :
a) the net unbalanced force on him is 'ma'
b) the normal reaction exerted by the floor on the man is m(g + a)
c) the apparent weight is greater than his true weight
View SolutionThe apparent weight of a man in a lift is W1 when lift moves upwards with some acceleration and is W2 when it is accerating down with same acceleration. Find the true weight of the man and acceleration of lift .
View SolutionTwo trolleys A and B are moving with accelerations a and 2a, respectively, in the same direction. To an observer in trolley A. Find the magnitude of the pseudo force acting on a block of mass m on trolley B.
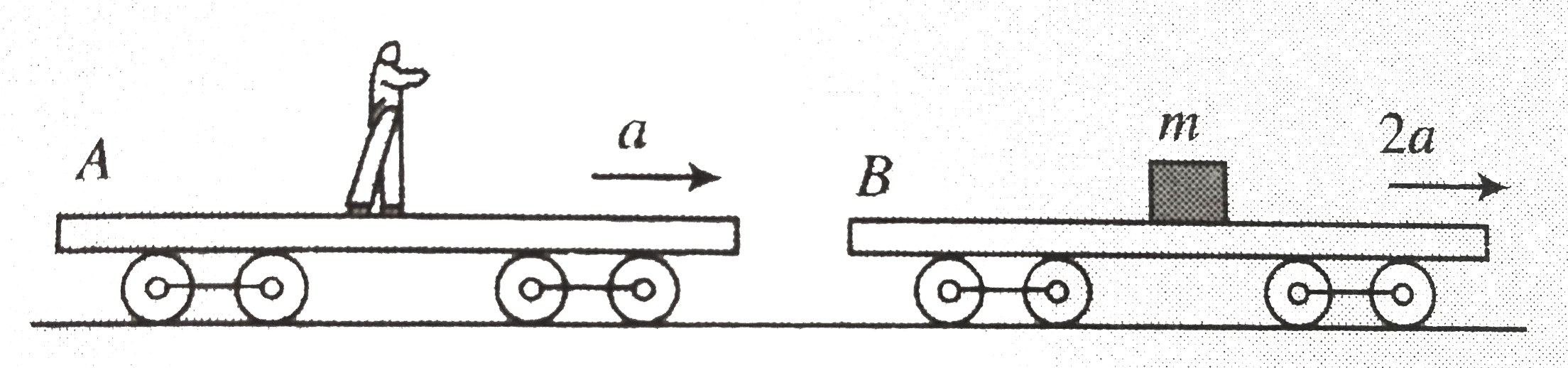
View SolutionA smooth block of mass m moves up from bottom to top of a wedge which is moving with an acceleration a10. Find the work done by the pseudo force measured by the person sitting at the edge of the wedge.

View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing on the ground are, respectively:
View Solution
