Two canoes are 10 m apart on a lake. Each bobs up and down with a period of 4.0 s. when one canoe is at its highest point, the other canoe is at its lowest point. Both canoes are always within a single cycle of the waves determine the speed of the wave.
The correct Answer is:B
To determine the speed of the wave created by the two canoes, we can follow these steps:
1. Identify the Period of the Wave:
The problem states that each canoe bobs up and down with a period (T) of 4.0 seconds.
T=4.0s
2. Calculate the Frequency of the Wave:
The frequency (f) is the reciprocal of the period. We can calculate it using the formula:
f=1T=14.0s=0.25Hz
3. Determine the Distance Between the Canoes:
The problem states that the two canoes are 10 m apart. When one canoe is at its highest point, the other is at its lowest point. This means they are separated by half of the wavelength (λ/2).
Distance=λ2=10m
4. Calculate the Wavelength:
From the distance, we can find the wavelength (λ) by rearranging the equation:
λ=2×Distance=2×10m=20m
5. Calculate the Speed of the Wave:
The speed (v) of the wave can be calculated using the formula:
v=f×λ
Substituting the values we found:
v=0.25Hz×20m=5m/s
Final Answer:
The speed of the wave created by the canoes is 5 m/s.
---
The problem states that each canoe bobs up and down with a period (T) of 4.0 seconds.
The frequency (f) is the reciprocal of the period. We can calculate it using the formula:
The problem states that the two canoes are 10 m apart. When one canoe is at its highest point, the other is at its lowest point. This means they are separated by half of the wavelength (λ/2).
From the distance, we can find the wavelength (λ) by rearranging the equation:
The speed (v) of the wave can be calculated using the formula:
The speed of the wave created by the canoes is 5 m/s.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple
26 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Two small boats are 10m apart on a lake. Each pops up and down with a period of 4.0 seconds due to wave motion on the surface of water. When one boat is at its highest point, the other boat is its lowest point. Both boats are always within a single cycle of the waves. The speed of the waves is:
View SolutionA simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
View SolutionA cork floating on the pond water executes a simple harmonic motion, moving up and down over a range of 4 cm. The time period of the motion is 1 s. at t=0, the cork is at its lowest position of oscillation, the position and velocity of the cork at t=10.5s, would be
View SolutionA thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length √3meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
View SolutionThe bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
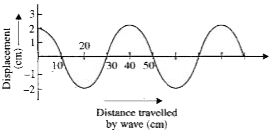
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
View SolutionA projectile is fired from a gun at an angle of 45∘ with the horizontal and with a speed of 20m/s relative to ground. At the highest point in its flight the projectile explodes into two fragments of equal masses. One fragement, whose initial speed is zero falls vertically. How far from the gun does the other fragment land, assuming a level terrain? Take g=10m/s2?
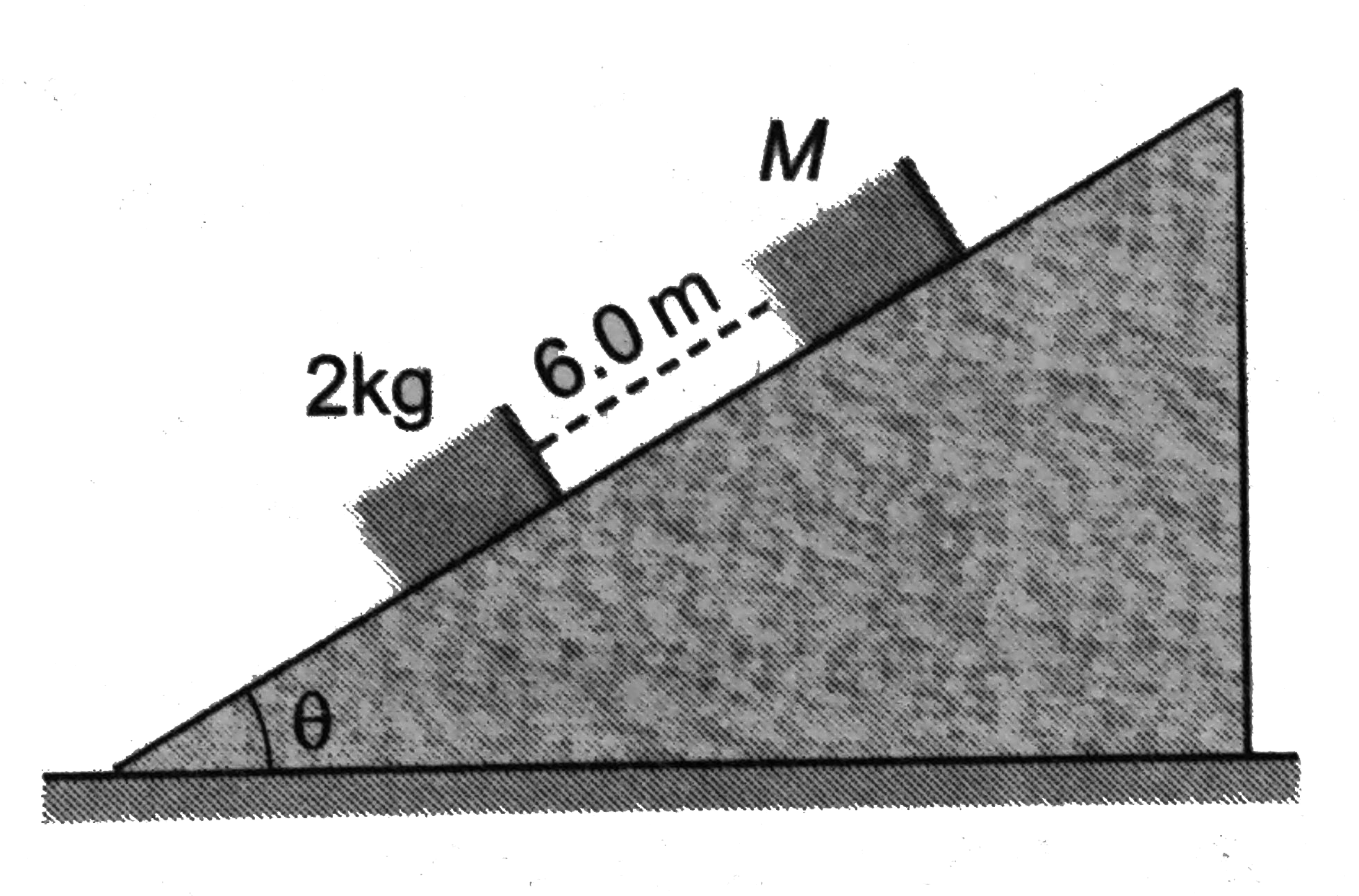
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
View SolutionThe given figure shows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.

(a) write down the equation of the curve.
(b) find the angle θ made by the tangent at point P with the x-axis.
(c ) If the particle at P has a velocity vpm/s, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave.
(d) find the frequency of the wave.
(e) find the displacement equation of the particle at the origin as a function of time.
(f) find the displacement equation of the wave.
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
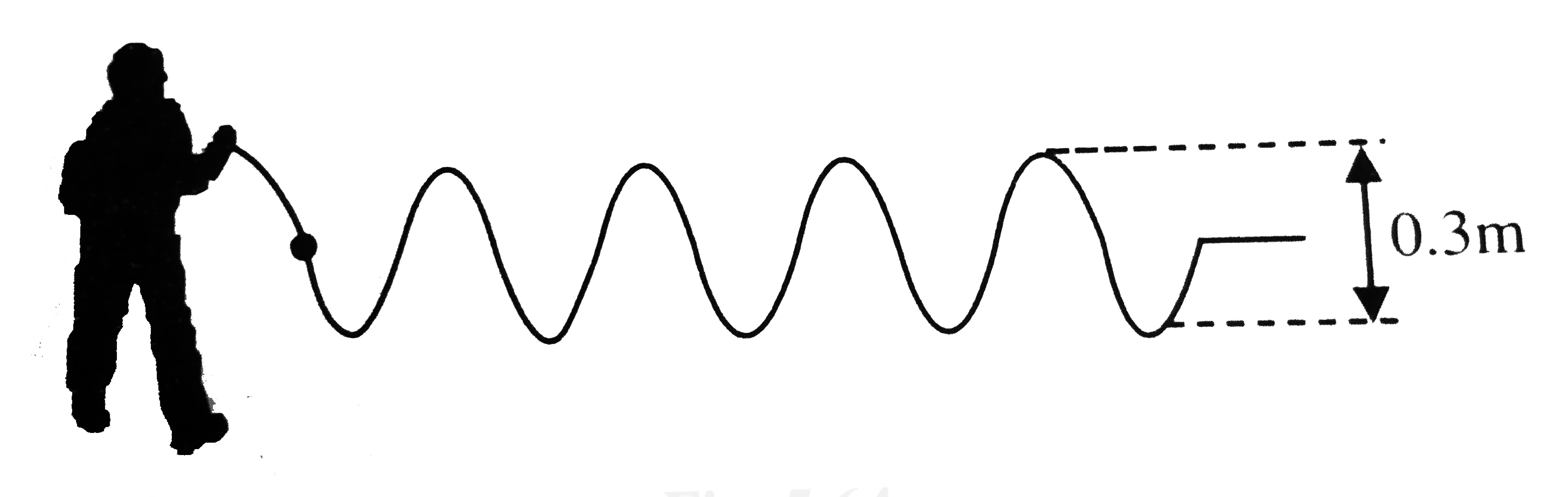
The amplitude of the wave is
View Solution
