A 40cm long brass rod is dropped one end first onto a hard floor but is caught before it topples over . With an 3kHz tone . The speed of sound in brass is
600m/s
1200m/s
2400m/s
4800m/s
The correct Answer is:C
To find the speed of sound in the brass rod, we can follow these steps:
Step 1: Understand the Problem
We have a brass rod that is 40 cm long, and it produces a sound with a frequency of 3 kHz when dropped. We need to find the speed of sound in brass.
Step 2: Convert Units
First, we convert the length of the rod from centimeters to meters:
- Length of the rod, L=40cm=0.4m
Step 3: Identify the Wave Properties
Since the rod is fixed at both ends when it is dropped, it can be modeled as a standing wave. The fundamental frequency (first harmonic) of a fixed rod has nodes at both ends.
Step 4: Relate Wavelength and Length
For a rod fixed at both ends, the length of the rod is equal to half the wavelength (λ) of the fundamental frequency:
L=λ2
Thus, we can express the wavelength as:
λ=2L
Step 5: Calculate the Wavelength
Substituting the length of the rod into the equation:
λ=2×0.4m=0.8m
Step 6: Use the Speed of Sound Formula
The speed of sound (v) is given by the formula:
v=f⋅λ
where f is the frequency. We need to convert the frequency from kHz to Hz:
f=3kHz=3000Hz
Step 7: Calculate the Speed of Sound
Now we can substitute the values of f and λ into the speed of sound formula:
v=3000Hz×0.8m=2400m/s
Step 8: Conclusion
The speed of sound in brass is 2400m/s.
We have a brass rod that is 40 cm long, and it produces a sound with a frequency of 3 kHz when dropped. We need to find the speed of sound in brass.
First, we convert the length of the rod from centimeters to meters:
- Length of the rod, L=40cm=0.4m
Since the rod is fixed at both ends when it is dropped, it can be modeled as a standing wave. The fundamental frequency (first harmonic) of a fixed rod has nodes at both ends.
For a rod fixed at both ends, the length of the rod is equal to half the wavelength (λ) of the fundamental frequency:
L=λ2
Thus, we can express the wavelength as:
λ=2L
Substituting the length of the rod into the equation:
λ=2×0.4m=0.8m
The speed of sound (v) is given by the formula:
v=f⋅λ
where f is the frequency. We need to convert the frequency from kHz to Hz:
f=3kHz=3000Hz
Now we can substitute the values of f and λ into the speed of sound formula:
v=3000Hz×0.8m=2400m/s
The speed of sound in brass is 2400m/s.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple
26 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
A steel rod 100 cm long is clamped at its centre. The fundmental frequency of longitudinal viberations of the rod are given to be 2.53kHz. What is the speed of sound is steel?
View SolutionA metal rod 40cm long is dropped on to a wooden floor and rebounds into air . Compressional waves of many frequencies are thereby set up in the rod . If the speed of compressional waves in the rod in 5500m/s, what is the lowest frequency of compressional waves to which the rod resonates as it rebounds?
View Solution
Knowledge Check
A pipe 17 cm long is closed at one end. Which harmonic mode of the pipe resonates a 1.5 kHz source? (Speed of sound in air = 340 m s−1)
AFirstBThirdCFifthDSeventhA pipe 30 cm long, is open at both ends. Which harmonic mode of the pipe resonates a 1.1 kHz source? (Speed of sound in air = 330 m s−1) a) First b) Third c) Second d) Fourth
AFirstBThirdCSecondDFourth
The air column in a pipe closed at one end is made to vibrate in its third over tone by tuning fork of frequency 220Hz. The speed of sound in air is 330m/sec. End correction may be neglected. Let P0 denote the mean pressure at any point in the pipe and ΔP0 the maximum amplitude of pressure vibration
Find the length of the air column
View SolutionA closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
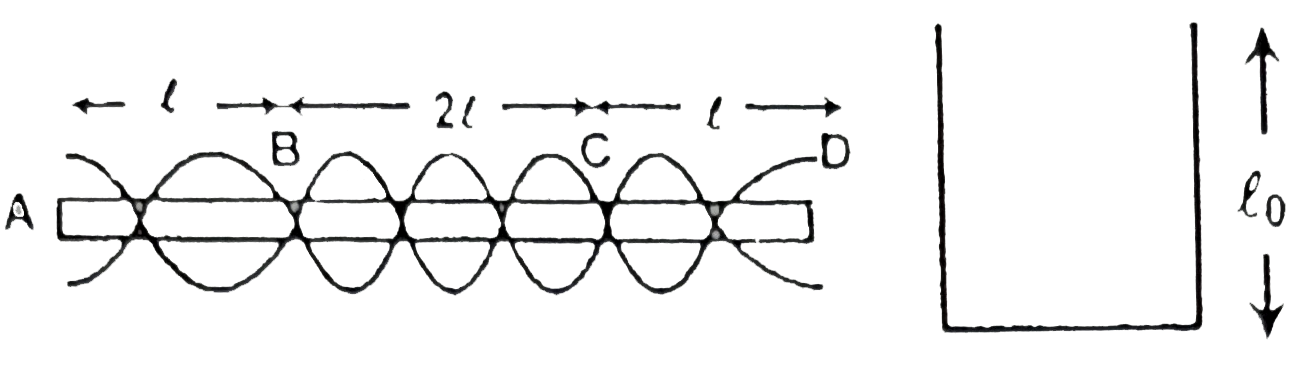
View SolutionA closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]

View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionA pipe 20cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430Hz source? Will the same source be in resonance with the pipe if both ends are open? Take speed of sound in air 340m/s.
View Solution
