A particle of mass m=1kg oscillates simple harmonically with angular frequency 1rad/s. Find the phase of the particle at t=1sand2s. Start calculating time when the particle moves up passing through the mean position.
To solve the problem step by step, we will follow the principles of simple harmonic motion (SHM) and the given parameters.
1. Understand the Problem: We have a particle of mass m=1kg that oscillates with an angular frequency ω=1rad/s. We need to find the phase of the particle at t=1s and t=2s, starting from when the particle is at the mean position (displacement x=0).
2. Displacement Equation: The displacement x of a particle in SHM can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
3. Determine the Phase Constant: At t=0, the particle is at the mean position, which means x(0)=0. Substituting t=0 into the displacement equation:
0=Asin(0+ϕ)
For this equation to hold true, sin(ϕ) must be zero. This occurs when ϕ=0 or ϕ=π (but we choose ϕ=0 for upward motion). Thus, we have:
ϕ=0
4. Simplify the Displacement Equation: With ϕ=0, the displacement equation simplifies to:
x(t)=Asin(ωt)
5. Substitute the Angular Frequency: Given ω=1rad/s, the equation becomes:
x(t)=Asin(t)
6. Find the Phase at t=1s: The phase of the particle at any time t can be represented as:
Phase=ωt
Therefore, at t=1s:
Phase at t=1s=1⋅1=1rad
7. Find the Phase at t=2s: Similarly, at t=2s:
Phase at t=2s=1⋅2=2rad
Final Answers:
- The phase of the particle at t=1s is 1rad.
- The phase of the particle at t=2s is 2rad.
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
0=Asin(0+ϕ)
For this equation to hold true, sin(ϕ) must be zero. This occurs when ϕ=0 or ϕ=π (but we choose ϕ=0 for upward motion). Thus, we have:
ϕ=0
x(t)=Asin(ωt)
x(t)=Asin(t)
Phase=ωt
Therefore, at t=1s:
Phase at t=1s=1⋅1=1rad
Phase at t=2s=1⋅2=2rad
- The phase of the particle at t=1s is 1rad.
- The phase of the particle at t=2s is 2rad.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.
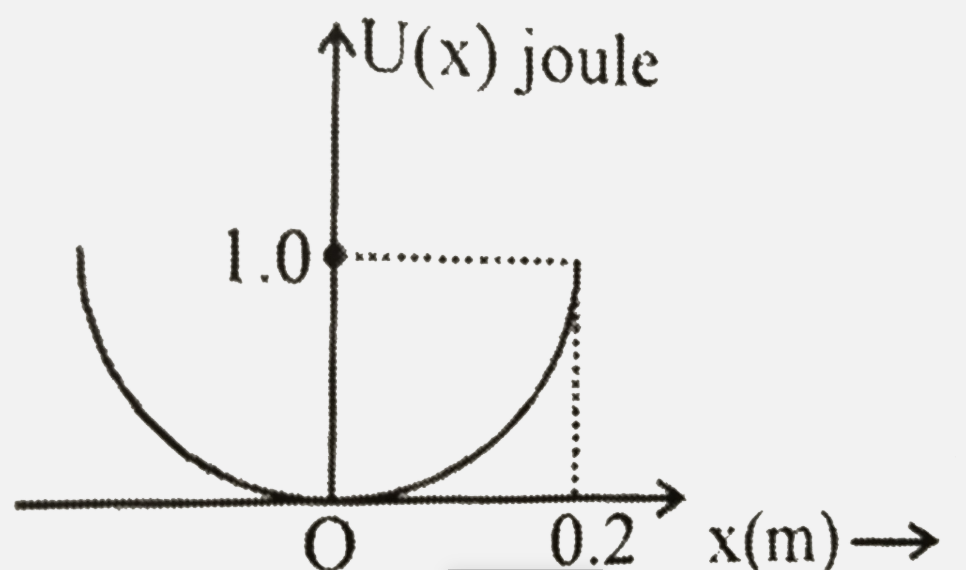
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass m=1kg excutes SHM about mean position O with angular frequency ω=1.0rad/s and total energy 2J. x is positive if measured towards right from O. At t=0, particle is at O and movel towards right.
View SolutionA particle executes simple harmonic motion with an amplitude of 4cm At the mean position the velocity of the particle is 10cm/s. distance of the particle from the mean position when its speed 5 cm/s is
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
