A flask of mercury is sealed off at 20∘C and is completely filled with mercury. If the bulk modulus for mercury is 250 Mpa and the coefficient of volume expansion of mercury is 1.82×10−4/∘C and the expansion of glass is ignored, the pressure of mercury within flask at 100∘C will be
100MPa
72MPa
36MPa
24MPa
The correct Answer is:C
To find the pressure of mercury within the flask at 100∘C, we can follow these steps:
Step 1: Identify the given values
- Initial temperature, T1=20∘C
- Final temperature, T2=100∘C
- Change in temperature, ΔT=T2−T1=100−20=80∘C
- Bulk modulus of mercury, B=250 MPa=250×106 Pa
- Coefficient of volume expansion of mercury, β=1.82×10−4 ∘C−1
Step 2: Calculate the change in volume
The change in volume ΔV can be calculated using the formula:
ΔV=V0⋅β⋅ΔT
Where V0 is the original volume of mercury in the flask. Since we are looking for the pressure change, we will keep V0 as a variable.
Substituting the values:
ΔV=V0⋅(1.82×10−4)⋅(80)
Calculating this gives:
ΔV=V0⋅1.456×10−2
Step 3: Use the bulk modulus to find the pressure change
The pressure change ΔP is given by the formula:
ΔP=−B⋅ΔVV0
Substituting ΔV from the previous step:
ΔP=−250×106⋅1.456×10−2V0V0
Here, V0 cancels out:
ΔP=−250×106⋅1.456×10−2
Calculating this gives:
ΔP=−250×1.456×104 Pa
ΔP=−364000 Pa=−364 kPa
Since pressure is typically expressed as a positive value, we take the absolute value:
ΔP=364 kPa=0.364 MPa
Step 4: Final pressure calculation
The initial pressure at 20∘C is atmospheric pressure, which is approximately 101.3 kPa. Therefore, the final pressure at 100∘C will be:
Pfinal=Pinitial+ΔP
Assuming Pinitial≈0 for the change:
Pfinal=0+0.364 MPa=0.364 MPa
Final Answer
The pressure of mercury within the flask at 100∘C will be approximately 0.364 MPa.
---
- Initial temperature, T1=20∘C
- Final temperature, T2=100∘C
- Change in temperature, ΔT=T2−T1=100−20=80∘C
- Bulk modulus of mercury, B=250 MPa=250×106 Pa
- Coefficient of volume expansion of mercury, β=1.82×10−4 ∘C−1
The change in volume ΔV can be calculated using the formula:
ΔV=V0⋅β⋅ΔT
Where V0 is the original volume of mercury in the flask. Since we are looking for the pressure change, we will keep V0 as a variable.
ΔV=V0⋅(1.82×10−4)⋅(80)
Calculating this gives:
ΔV=V0⋅1.456×10−2
The pressure change ΔP is given by the formula:
ΔP=−B⋅ΔVV0
Substituting ΔV from the previous step:
ΔP=−250×106⋅1.456×10−2V0V0
Here, V0 cancels out:
ΔP=−250×106⋅1.456×10−2
Calculating this gives:
ΔP=−250×1.456×104 Pa
ΔP=−364000 Pa=−364 kPa
Since pressure is typically expressed as a positive value, we take the absolute value:
ΔP=364 kPa=0.364 MPa
The initial pressure at 20∘C is atmospheric pressure, which is approximately 101.3 kPa. Therefore, the final pressure at 100∘C will be:
Pfinal=Pinitial+ΔP
Assuming Pinitial≈0 for the change:
Pfinal=0+0.364 MPa=0.364 MPa
The pressure of mercury within the flask at 100∘C will be approximately 0.364 MPa.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
Mercury has a small coefficient of volume expansion.
View SolutionCoefficient of volume expansion of mercury is 0.18×10−3/.∘C. If the density of mercury at 0∘C is 13.6g/cc, then its density at 200∘C is
View SolutionA flask of volume 103 cc is completely filled with mercury at 0∘C The coefficient of cubical expansion of mercury is 180×10−6/∘C and heat of glass is 40×10−6/∘C. If the flask in now placed in boiling water at 100∘C how much mercury will overflow?
View SolutionA glass flask of volume one litre at 0∘C is filled, level full of mercury at this temperature. The flask and mercury are now heated to 100∘C. How much mercury will spill out if coefficient of volume expansion of mercury is 1.82×10−4/∘C and linear expansion of glass is 0.1×10−4/∘C respectively?
View SolutionCoefficient of apparent expansions of mercury is 0.18×10−3/0C. If the density of mercury at 00C is 13.6g/cc its density at 473K will be
View SolutionThe bulk modulus of mercury is 2.8×1010 N/m2 and the density is 13600 kg/m2. What is the speed of sound in mercury ?
View SolutionA glass cylinder contains m0=100g of mercury at a temperature of t0=0∘C. When temperature becomes t1=20∘C the cylinder contains m1=99.7g of mercury The coefficient of volume expansion of mercury γHe=18×(10−5/∘C Assume that the temperature of the mercury is equal to that of the cylinder. The coefficient of linear expansion of glass α is
View SolutionA glass cylinder contains m0=100g of mercury at a temperature of t0=0∘C. When temperature becomes t1=20∘C the cylinder contains m1=99.7g of mercury The coefficient of volume expansion of mercury γHe=18×(10−5/∘C Assume that the temperature of the mercury is equal to that of the cylinder. The corfficient of linear expansion of glass α is
View SolutionState true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
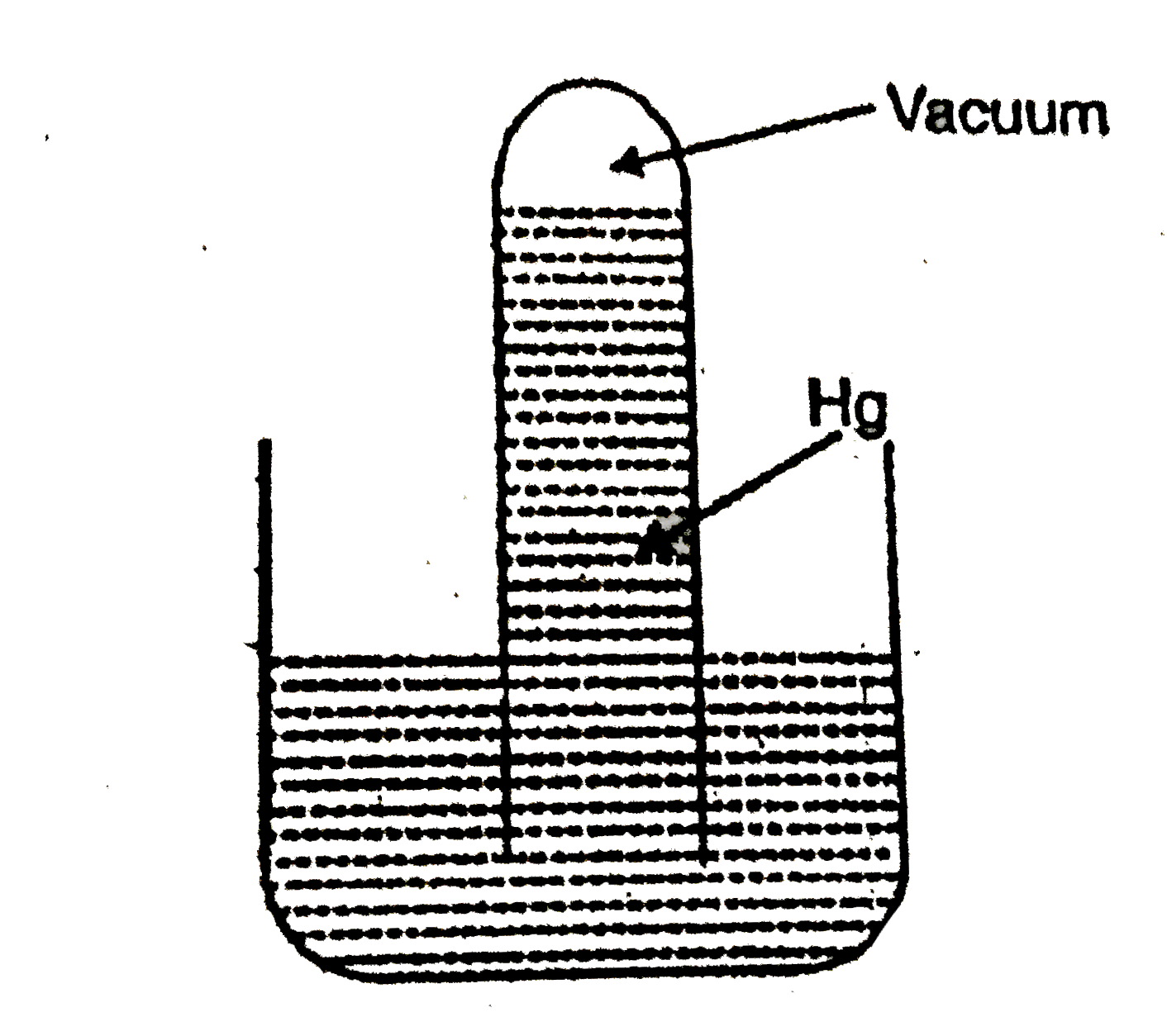
View SolutionA glass vessel of volume 100cm3 is filled with mercury and is heated from 25∘C→75∘C. What volume of mercury will overflow? Coefficient of linear expansion of glass =1.8×10−6/'∘C and coefficeient of volume expansion of mercury is 1.8×10−4/'∘C.
View Solution
