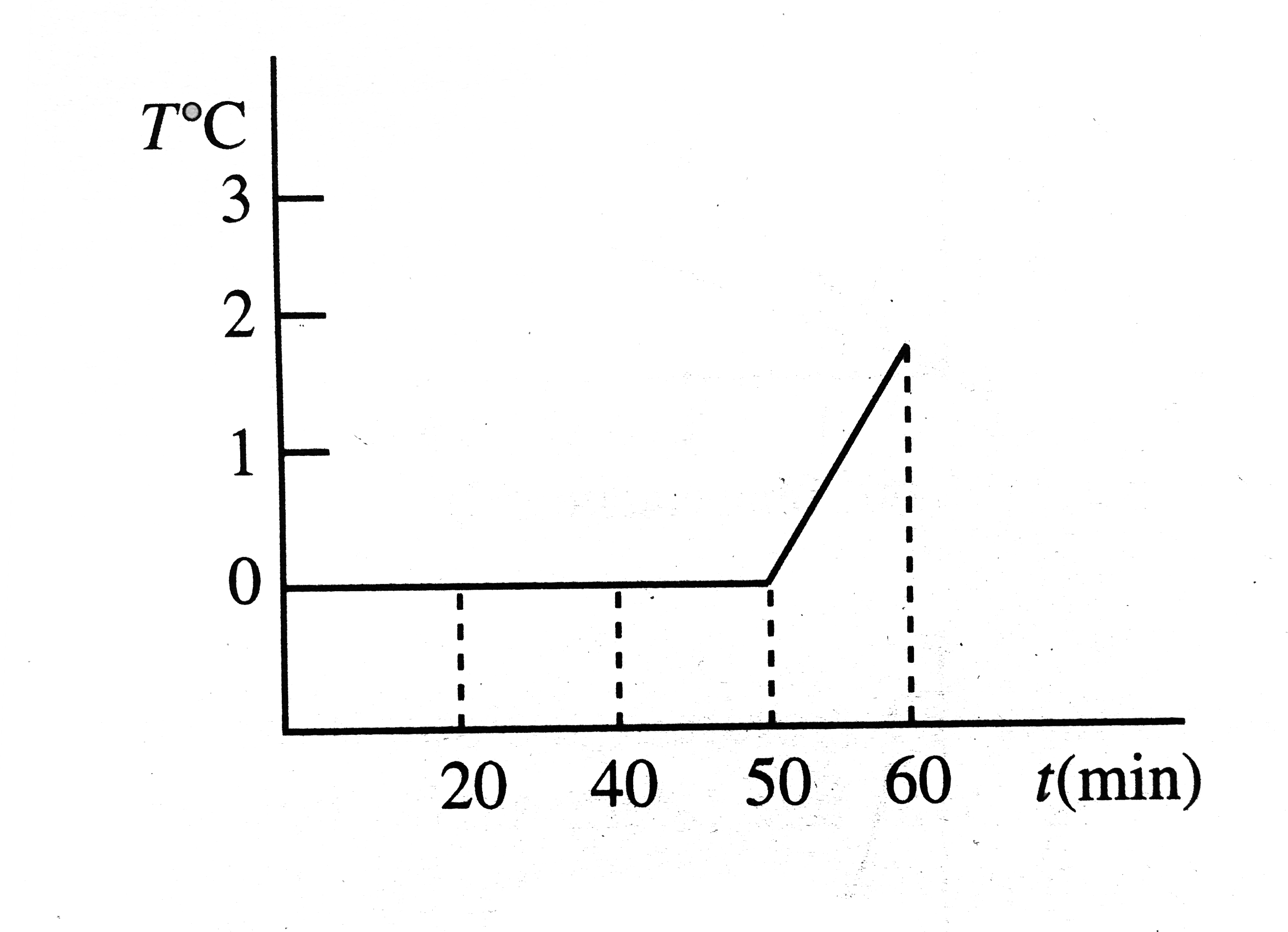
A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at $0^{\circ} C$ at time $t = 0$ . The temperature of the mixture is measured at various times and the result is plotted as shown in Fig. During the first 50 min the mixture remains at $0^{\circ} C$ . From 50 min to 60 min, the temperature increases to $2^{\circ} C$ Neglecting the heat capacity of the vessel, the initial mass of the ice is

A

$\frac{10}{7} k g$

B

$\frac{5}{7} k g$

C

$\frac{5}{4} k g$

D

$\frac{5}{8} k g$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let m be the mass of ice.
Rate of heat given by the burner is constant.
In the first 50 min
$\frac{d Q}{d t} = \frac{m L}{t_{1}} = \frac{m k g \times (80 \times 4.2 \times 10^{3}) J / k g}{(50 min)}$ .(i)
From 50 min to 60 min
$\frac{d Q}{d t} = \frac{(m + 5) S_{H_{2} O} Δ θ}{t_{2}}$
$= \frac{(m + 5) k g (4.2 \times 10^{3}) J / k g \times 2^{\circ} C}{10 min}$ ..(ii)
From Eqs. (i) and (ii)
$\frac{80 m}{50} = \frac{2 (m + 5)}{10}$
$7 m = 5 \Rightarrow m = \frac{5}{7} k g = 0.7 k g$

Updated on:21/07/2023

|

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-CALORIMETRY-Single Correct

Home
Ask Doubt
Profile