Find the current passing through battery immediately after key (K) is closed. It is given that initially all the capacitors are uncharged. (Given that R=6Ω and C=4μF)
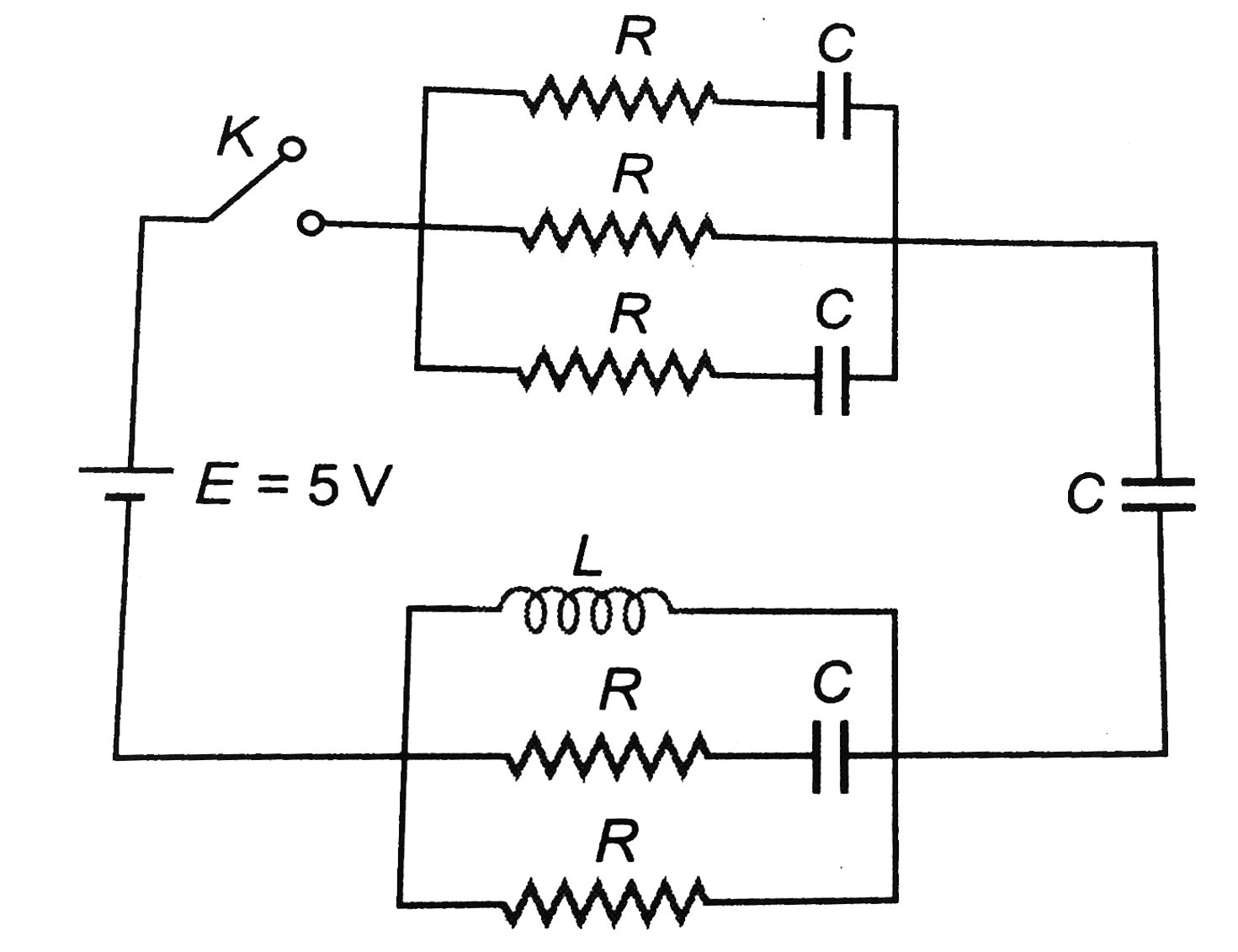
1A
5A
3A
2A
The correct Answer is:A
Req=5R6⇒I=6E5R=1A
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
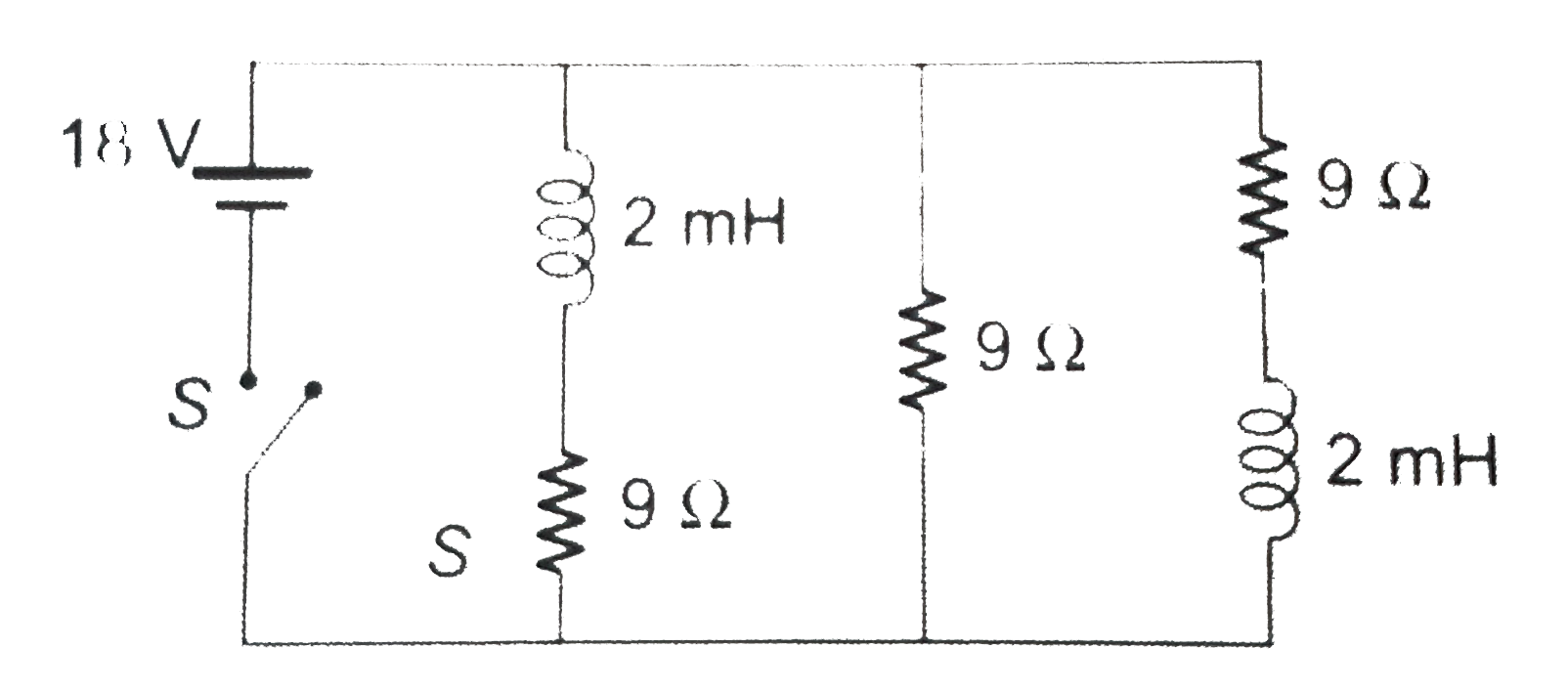
In the circuit diagram the current through the battery immediately after the switch S is closed is
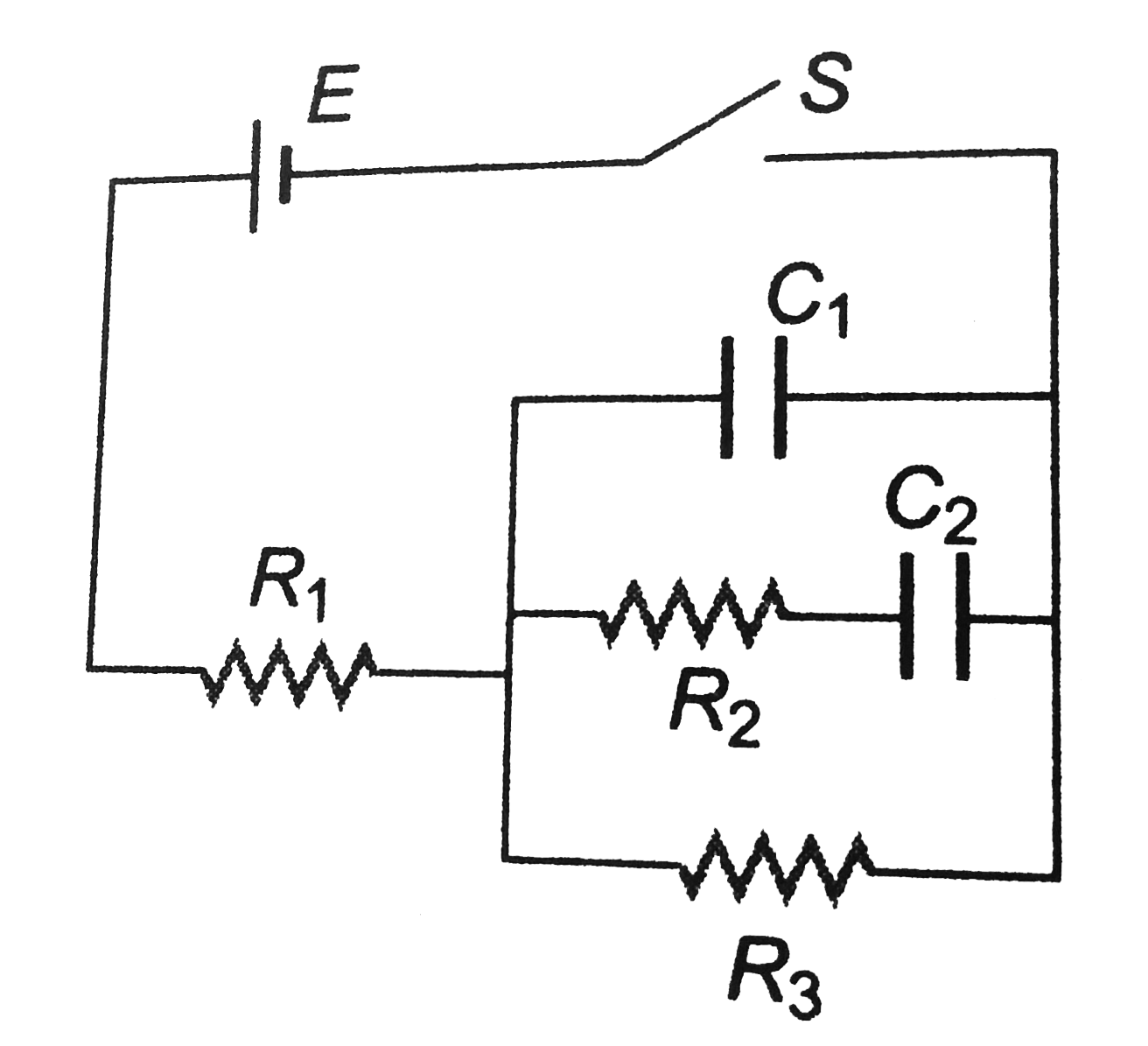
View SolutionThe current through the battery just after the switch S is Closed is (the capacitors are initially uncharged )
_PHY_E01_002_Q01.png)
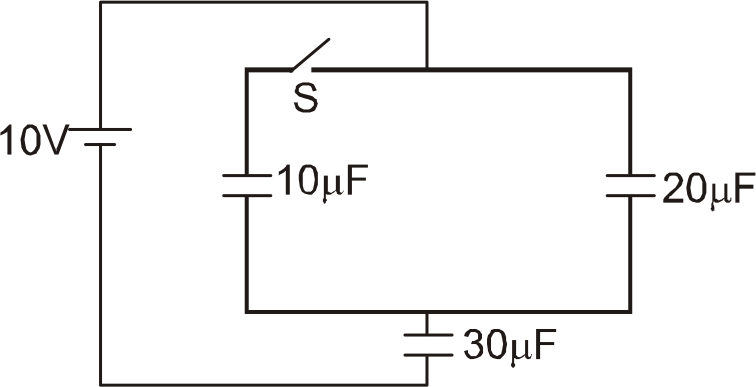
View SolutionCharge flow through the battery after closing the switch is (initially all capacitors are uncharged) :
View SolutionFind the current through the battery
(i) just after the switch is closed.
(ii) long after the switch has been closed.
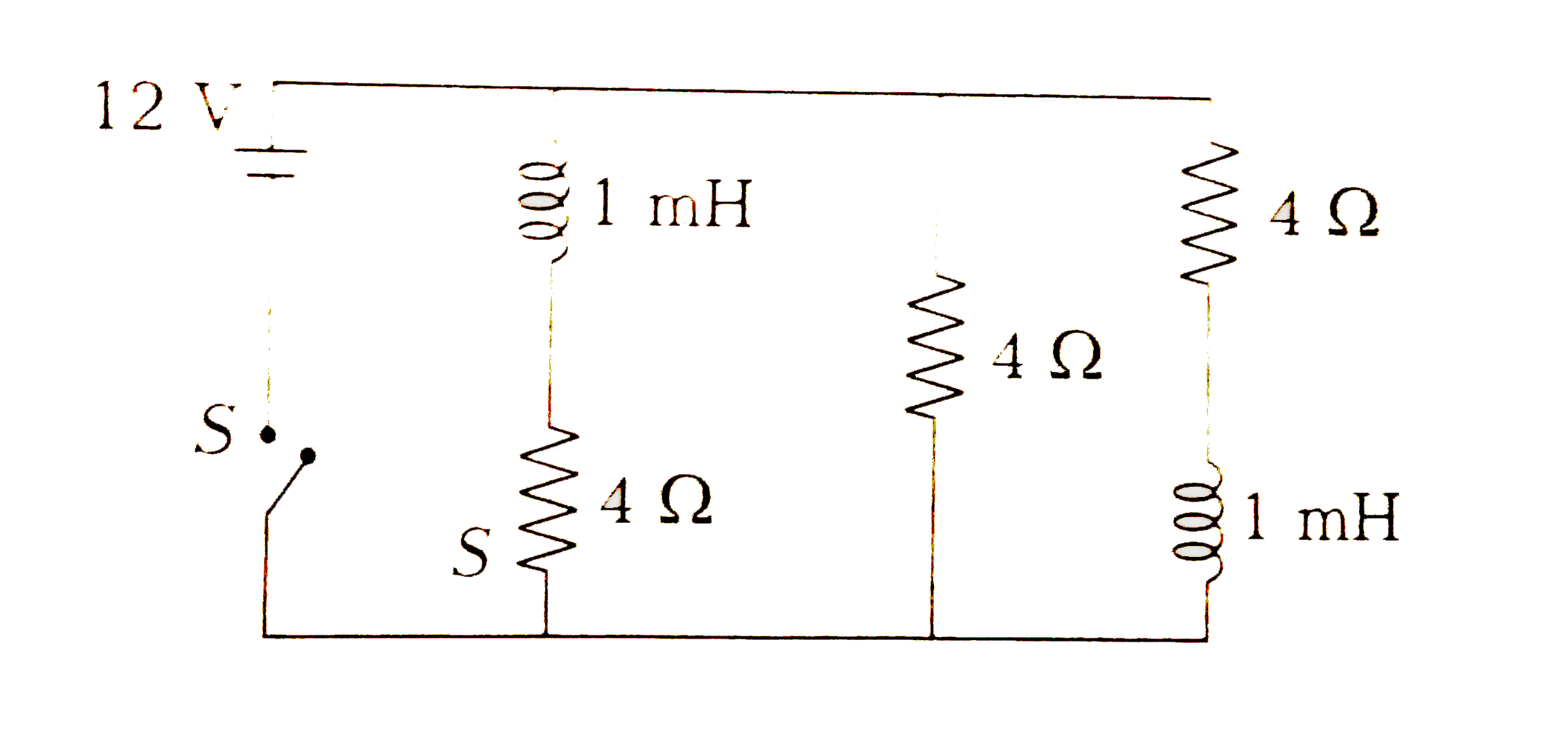
View Solution(i) Find the total charge flown through the battery in the arrangement shown in figure after switch S is closed (initially all the capacitors are uncharged).
(ii) Find out final charge on each capacitor.

View SolutionFind current through the battery
(a) just after the switch is closed
(b) long after the switch has been closed
View SolutionIn the figure given below, the current passing through 6Ω resistor is
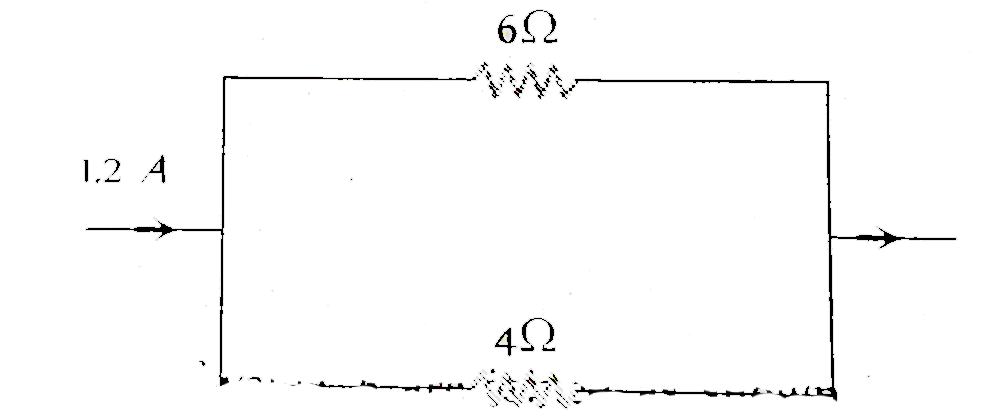
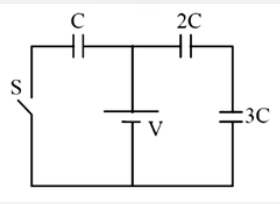
View SolutionIn the given diagram. Find the heat generated on closing the switch S (Initially the capacitor of capacitance C is uncharged ) -
View SolutionA capacitor C(=100μF) is charged with a total charge of 1.2×10−3C and connected in a circuit as shown. Find the current in the circuit after the key k is closed ( t= 0) as a function of time (t). Notice that the positively charged plate of the capacitor is connected to the negative terminal of the cell

View SolutionFigure shows a LCR circuit connected with a battery emf ε and internal resistance 'R'. After a long time (initially the capacitor was uncharged)

View Solution
