A closed circuit of a resistor , inductor of inductance and a source of emf are connected is series. If the inductance of the coil is abruptly decreaed to (by removing its magnetic core), the new current immediately after this moment is (before decreasing the inductance the circuit is in steady state)
zero
The correct Answer is:C
To solve the problem, we need to analyze the circuit before and after the inductance change. Here’s a step-by-step solution:
Step 1: Determine the initial current in the circuit
In a steady state, the current through the circuit can be calculated using Ohm's law. The total voltage in the circuit is equal to the EMF (E) provided by the source.
The initial current I0 in the circuit can be given by:
I0=ER
Step 2: Understand the effect of changing inductance
When the inductance L is abruptly decreased to L4, the inductor will try to maintain the current flowing through it due to its property of opposing changes in current.
Step 3: Apply the inductor's property
The inductor's property states that the voltage across the inductor is given by:
VL=Ldidt
Since the inductance is changed abruptly, we can assume that the change in current di happens over an infinitesimally small time dt.
Step 4: Calculate the new current immediately after the change
At the moment the inductance changes, the inductor will still have the same current flowing through it as it did just before the change. Therefore, we can set up the equation:
E=Ldidt+RI
However, since the inductance has changed to L4, we can express the voltage across the inductor just after the change as:
E=L4didt+RI
At the moment of change, I is still I0, so we can substitute I0 into the equation:
E=L4⋅0+RI0
This means that the current immediately after the change remains the same as it was before the change, which is:
I=I0=ER
Step 5: Conclusion
Thus, the new current immediately after the inductance is decreased to L4 is:
I=ER
Final Answer
The new current immediately after the change is ER.
In a steady state, the current through the circuit can be calculated using Ohm's law. The total voltage in the circuit is equal to the EMF (E) provided by the source.
I0=ER
When the inductance L is abruptly decreased to L4, the inductor will try to maintain the current flowing through it due to its property of opposing changes in current.
The inductor's property states that the voltage across the inductor is given by:
VL=Ldidt
Since the inductance is changed abruptly, we can assume that the change in current di happens over an infinitesimally small time dt.
At the moment the inductance changes, the inductor will still have the same current flowing through it as it did just before the change. Therefore, we can set up the equation:
E=Ldidt+RI
However, since the inductance has changed to L4, we can express the voltage across the inductor just after the change as:
E=L4didt+RI
At the moment of change, I is still I0, so we can substitute I0 into the equation:
E=L4⋅0+RI0
This means that the current immediately after the change remains the same as it was before the change, which is:
I=I0=ER
Thus, the new current immediately after the inductance is decreased to L4 is:
I=ER
The new current immediately after the change is ER.
Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (multiple Correct )
Explore 7 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (assertion-reasoning)
Explore 2 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (subjective)
Explore 7 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
Similar Questions
A coil of self-inductance L is connected in series with a bulb B and an AC source. Brightness of the bulb decreases when
View SolutionA circuit contains two inductors of self-inductance L1 and L2 in series (Fig) If M is the mutual inductence, then the effective inductance of the circuit shows will be

View Solution
Knowledge Check
Two inductors of inductance L each are connected in series with opposite magnetic fluxes. The resultant inductance is
(Ignore mutual inductance)AzeroBLC2LD3L
An AC circuit consists of an inductor of inductance 0.5H and a capacitor of capacitance 8μF in series. The current in the circuit is maximum when the angular frequency of AC source is
View SolutionA closed circuit consists of a source of constant emfE and a choke coil of inductance L connected in series.The active resistance of the whole circuit is equal to R.It is in steady state.At the moment L=0 the choke coil inductance was decreased abruptly 4 times.The current in the circuit as a function of time t is ER[1−xc−4tR/L].Find out value of x.
View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionAn inductor of inductance L and ressistor of resistance R are joined in series and connected by a source of frequency ω. Power dissipated in the circuit is
View SolutionIn the circuit, a battery of emf E, a resistance R and inductance coil L1andL2 and switch S are connected as shown. In Fig. Initially the switch is open
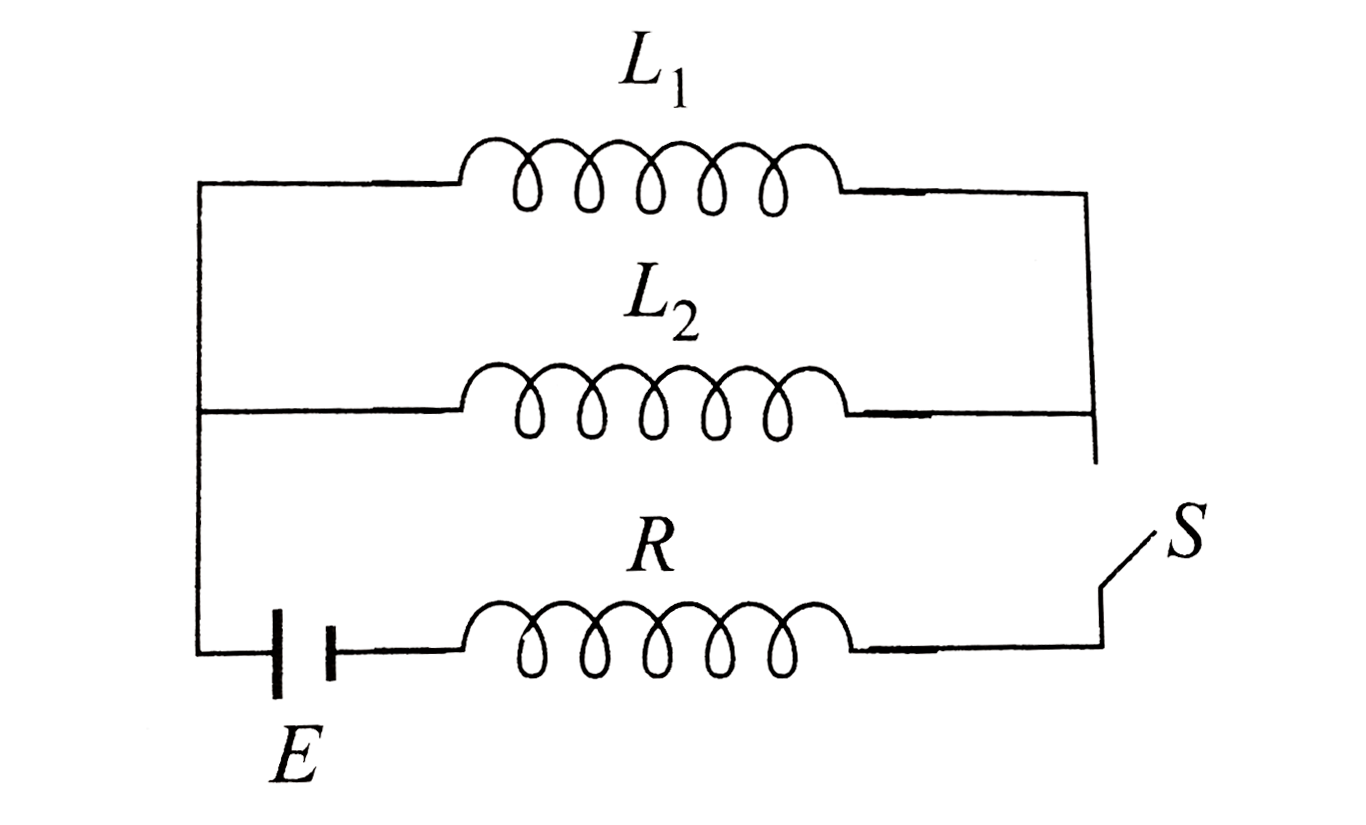
View SolutionAn inductor of inductance L = 8 H and a resistor of resistance R = 2Ω are connected in series with a battery of emf E = 10 V as shown in the figure. If the switch is closed at t = 0, then the voltage drop across the inductor at t = 1 s will be in volts)
View SolutionAn inductance L and a resistance R are first connected to a battery. After some time the battery is disconnected but L and R remain connected in a closed circuit. Then the current reduces to 37% of its initial value in
View Solution