A magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of heat the generated in the loop during that time
(a) aT3R
(b) a2T23R
( c) a2T2R
( d) a2T33R
The correct Answer is:D
(D) Given that ϕ=at(T−t)
Induced emf, E=dϕdt=ddt[at(T−t)]
=at(0−1)+a(T−t)
=a(T−2t)
So, induced emf is also a function of time.
∴ Heat generated in time T is
H=∫T0E2Rdt=a2R∫T0(T−2t)2dt=a2T33R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
View SolutionThe magnetic field through a single loop of wire, 12cm in radius and of 8.5Ω resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) t=0 to t=2.0s (b) t=2.0s to t=4.0s (c) t=4.0s to t=6.0s.
The magnetic field is perpendicular to the plane of the loop.
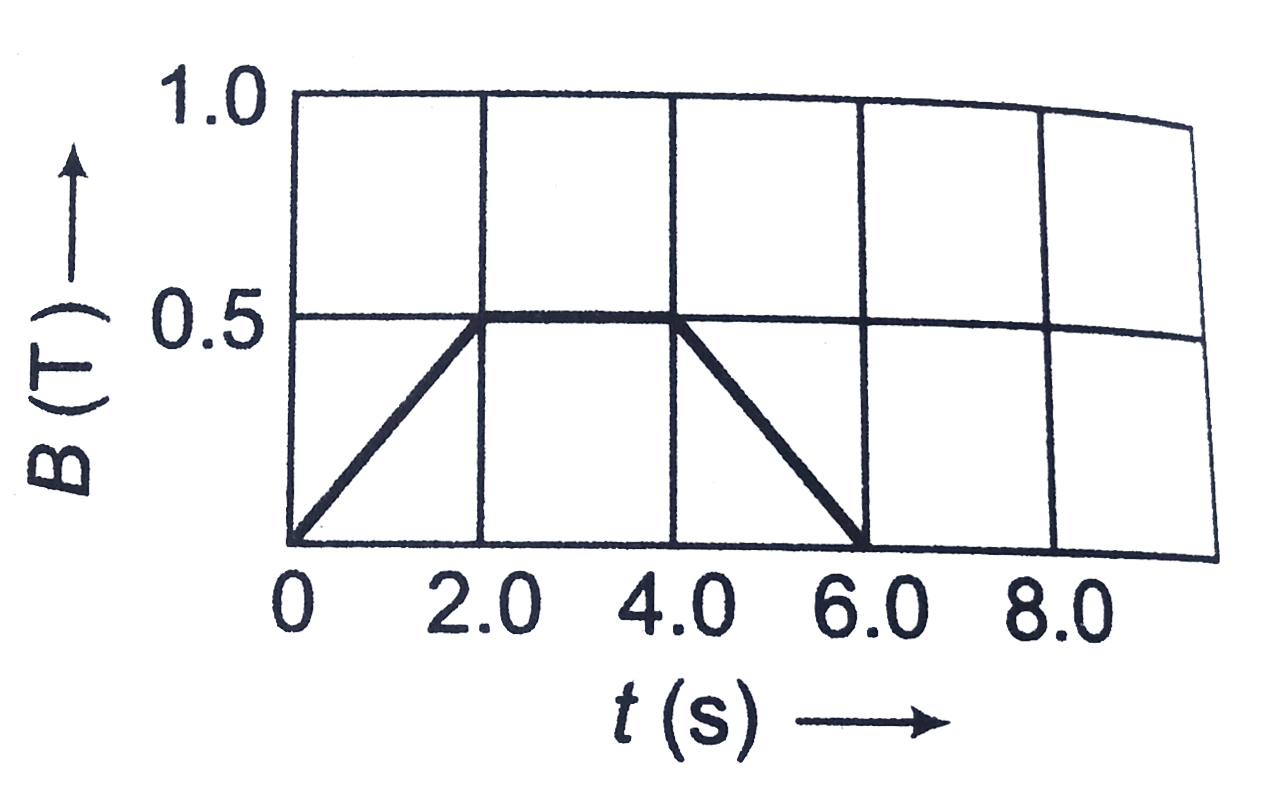
View Solution
Knowledge Check
The charge flowing through a resistance R varies with time t as Q=at−bt2. The total heat produced in R is
Aa3RbBa3R2bCa3R3bDa3R6bThe magnetic flux through a coil perpendicluar to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 V
Current passing through a resistor of resistance 5Ω varies with time as shown in the graph.Heat generated in the resistance during 3s is equal to
_PHY_E05_283_Q01.png)
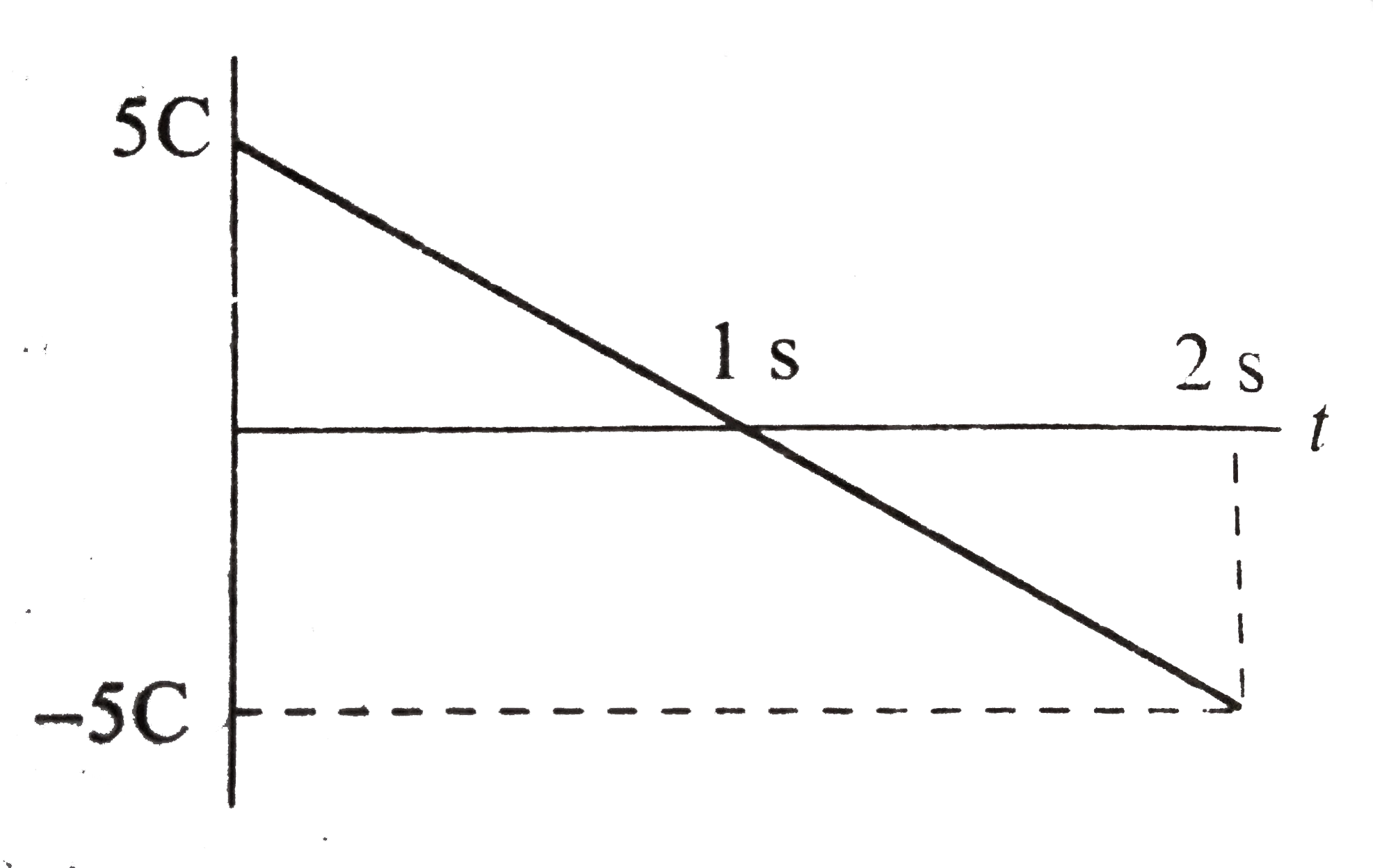
View SolutionA charge passing through a resistor varies with time as shown in the figure. The amount of heat generated in time t is best represented (as a function of time ) by
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View SolutionA triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be :

View SolutionThe charge Q( in coulomb) flowing through a resistance R=10Ω varies with time t (in second) as Q=2t−t2 . The total heat produced in resistance R is
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View Solution
