A copper rod is bent inot a semi-circle of radius a and at ends straight parts are bent along diameter of the semi-circle and are passed through fixed, smooth and conducting ring O and O' as shown in figure. A capacitor having capacitance C is connected to the rings. The system is located in a uniform magnetic field of induction B such that axis of rotation OO' is perpendicular to the field direction. At initial moment of time (t=0), plane of semi-circle was normal to the field direction and the semi-circle is set in rotation with constant angular velocity ω. Neglect the resistance and inductance of the circuit. The current flowing through the circuit as function of time is

(a) 14πω2a2Cbcosωt
( b) 12πω2a2CBcosωt
( c) 14πω2a2CBsinωt
(d) 12πω2a2CBsinωt
The correct Answer is:B
(b) When the copper rod is rotated, flux linked with the circuit varies with time.
Therefore, an emf is induced in the circuit.
At time t, plane of semi-circle makes angle ωt with the plane of rectangular part of the circuit. Hence, comonent of the magnetic inducetion normal to plane of semi-circle is equal to Bcosωt.
ϕ1=12πa2Bcosωt
Let area of rectangular part of the circuit be A.
∴ Flux linked with this part is
ϕ2=BA
∴ Total flux linked with the circuit is
ϕ=12πa2Bcos(ωt)+BA
∴ Induced emf in the circuit,
e=−dϕdt=12πωa2Bsin(ωt)
Since resistance of the circuit is negligible, therefore, potential difference acroos the capacitor is equal to induced emf in the circuit.
∴ Change on the capacitor at time t is q=Ce
=12πωa2CBsin(ωt)
But current I=dqdt=12πω2a∘CBcos(ωt)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
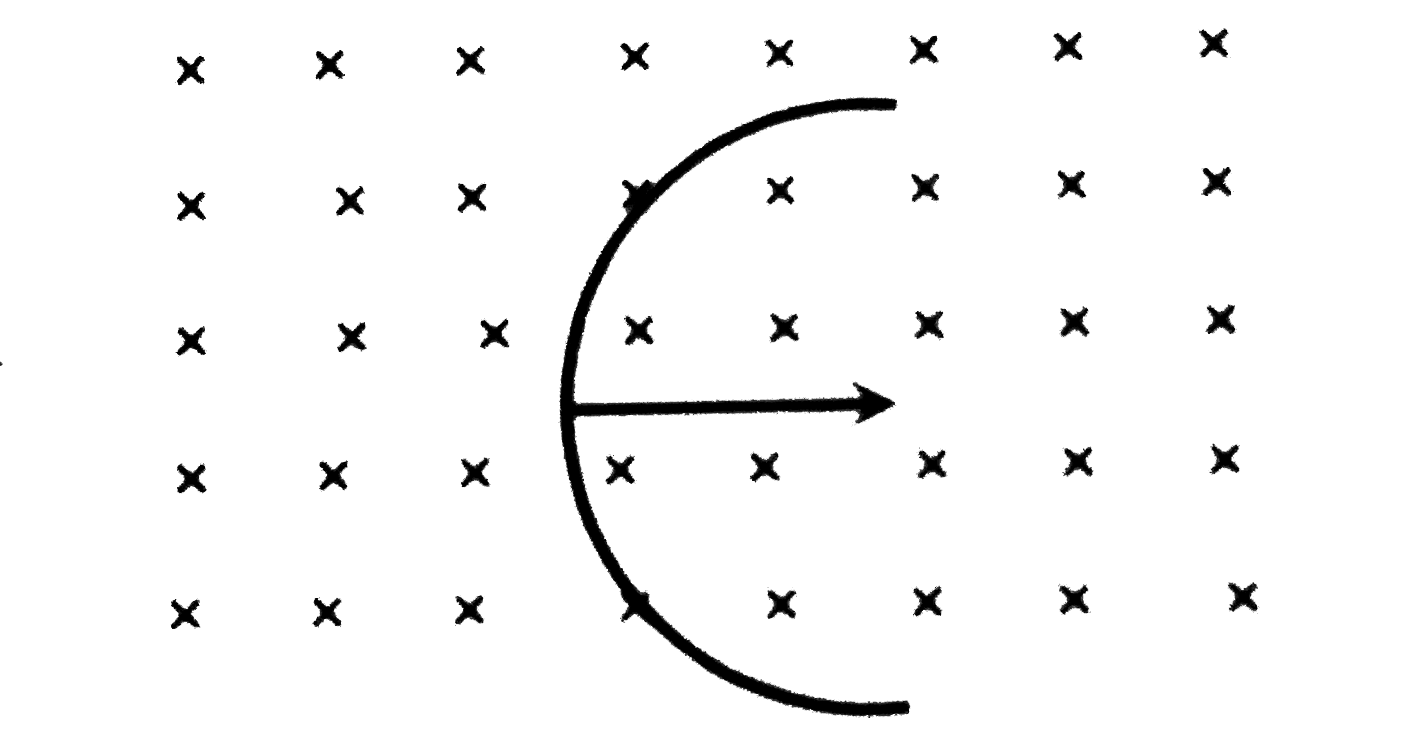
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
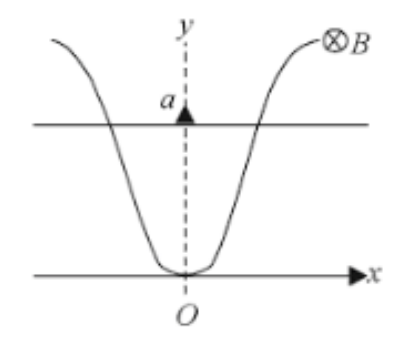
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View SolutionA wire is bent to form a semi-circle of radius a. the wire rotates about its one end with angular velocity ω.Axis of rotation being perpendicular to plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the axis of rotation as shown . The correct statement is :
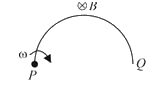
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View Solution

