Two identical sources each of intensity I0 have a separation d=λ/8, where λ is the wavelength of the waves emitted by either source. The phase difference of the sources is π/4 The intensity distribution I(θ) in the radiation field as a function of θ Which specifies the direction from the sources to the distant observation point P is given by
I(θ)=I0cos2θ
I(θ)=I04cos2(πθ8)
I(θ)=4I0cos2[π8(sinθ+1)]
I(θ)=I0sin2θ
The correct Answer is:c
To solve the problem, we need to derive the intensity distribution I(θ) in the radiation field as a function of the angle θ for two coherent sources with given conditions. Here’s a step-by-step solution:
Step 1: Understand the parameters
We have two identical sources, each with intensity I0. The separation between the sources is given by d=λ8, where λ is the wavelength of the emitted waves. The phase difference between the two sources is Δϕ=π4.
Step 2: Calculate the path difference
The path difference Δx between the two waves reaching a point P at an angle θ can be expressed as:
Δx=dsinθ
Substituting d:
Δx=λ8sinθ
Step 3: Relate path difference to phase difference
The phase difference Δϕ due to the path difference can be calculated using the formula:
Δϕ=2πλΔx
Substituting Δx:
Δϕ=2πλ(λ8sinθ)=π4sinθ
Step 4: Total phase difference
The total phase difference ϕ at point P is the sum of the initial phase difference and the phase difference due to path difference:
ϕ=Δϕ+initial phase difference=π4+π4sinθ
Step 5: Calculate the intensity
The intensity I(θ) at point P for two coherent sources can be expressed as:
I(θ)=4I0cos2(ϕ2)
Substituting for ϕ:
I(θ)=4I0cos2(12(π4+π4sinθ))
This simplifies to:
I(θ)=4I0cos2(π8(1+sinθ))
Final Expression
Thus, the intensity distribution I(θ) is given by:
I(θ)=4I0cos2(π8(1+sinθ))
We have two identical sources, each with intensity I0. The separation between the sources is given by d=λ8, where λ is the wavelength of the emitted waves. The phase difference between the two sources is Δϕ=π4.
The path difference Δx between the two waves reaching a point P at an angle θ can be expressed as:
Δx=dsinθ
Substituting d:
Δx=λ8sinθ
The phase difference Δϕ due to the path difference can be calculated using the formula:
Δϕ=2πλΔx
Substituting Δx:
Δϕ=2πλ(λ8sinθ)=π4sinθ
The total phase difference ϕ at point P is the sum of the initial phase difference and the phase difference due to path difference:
ϕ=Δϕ+initial phase difference=π4+π4sinθ
The intensity I(θ) at point P for two coherent sources can be expressed as:
I(θ)=4I0cos2(ϕ2)
Substituting for ϕ:
I(θ)=4I0cos2(12(π4+π4sinθ))
This simplifies to:
I(θ)=4I0cos2(π8(1+sinθ))
Thus, the intensity distribution I(θ) is given by:
I(θ)=4I0cos2(π8(1+sinθ))
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Multiple Correct
Explore 8 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Subjective
Explore 11 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
Similar Questions
Two identical radiators have a separation of d=λ/4 where λ is the wavelength of the waves emitted by either source. The initial phase difference between the sources is π/4. Then the intensity on the screen at a distant point situated at an angle θ=30∘ from the radiators is (here I0 is intensity at that point due to one radiator alone)
View SolutionTwo light sources with intensity I0 each interfere in a medium where phase difference between them us π2. Resultant intensity at the point would be.
View SolutionFour monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View SolutionIn Youngs double slit experiment, the phase different between two coherent sources of equal intensity is π/3.The intensity at a point which is at equal distance from the two slits is (l0 is maximum intensity)
View SolutionTwo coherent sources each emitting light of intensity I0 Interfere, in a medium at a point, where phase different between them is 2π3. Then, the resultant intensity at that point would be.
View SolutionTwo point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources ?
View SolutionS1 and S2 in List I represent coherent point sources, S represents a point source λ = wavelength of light emitted by the sources. Fringe pattern is observed on the screen. Exclude the position of source while detecting the fringe pattern.
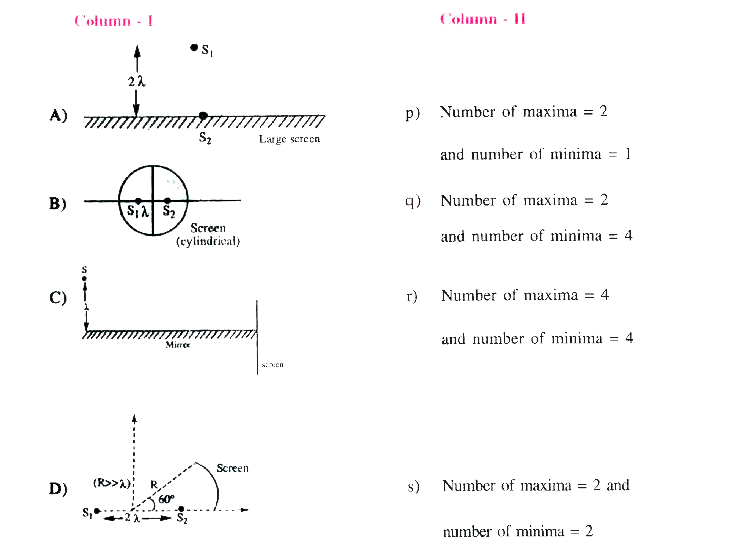
View SolutionTwo sources of intensity I and 4I are used in an interference experiment. Find the intensity at a point where the waves from two sources superimpose with a phase difference of (a) zero, (b) π/2, (c ) π and (d) ratio of maximum and minimum intensity.
View SolutionTwo identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.
View SolutionTwo incoherent sources of light emitting light of intensity I0 and 3I0 interfere in a medium. Calculate, the resultant intensity at any point.
View Solution