A slab of water is on the top of a glass slab of refractive index 2. At what angle to the normal must a ray be incident on the top sureface of th eglass slab so that it is reflected from the bottom surface as shown in figure ?
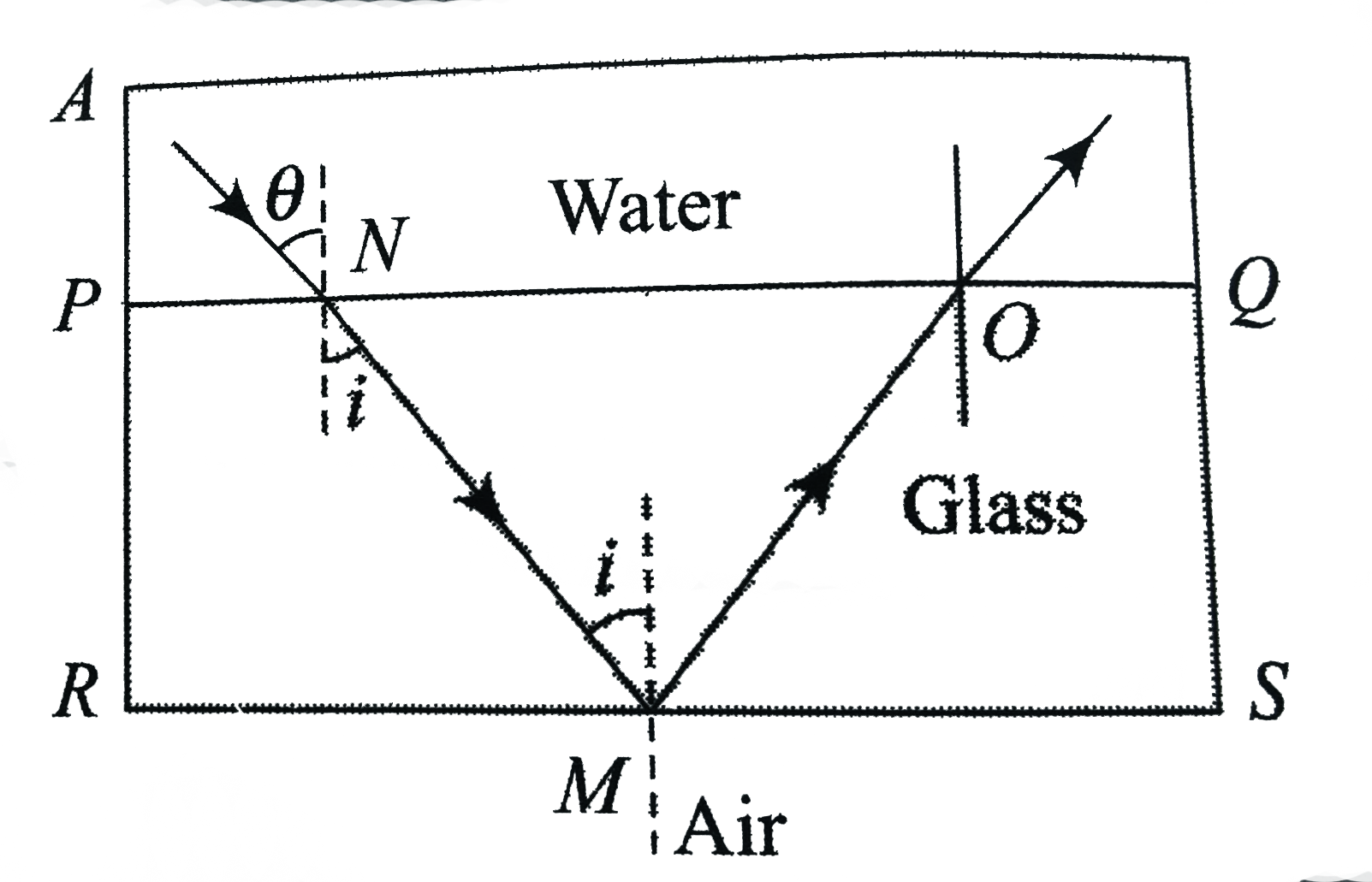
$A slab of water is on the top of a glass slab of refractive index 2. At what angle to the normal must a ray be incident on the top sureface of th eglass slab so that it is reflected from the bottom surface as shown in figure ?$

Video Solution

Text Solution

Verified by Experts

For the light ray to be reflected from the lower surface RS, the angle of incidence must be greater than the critival angle for the glass-air interface (at N).
$i > {sin}^{- 1} (\frac{1}{2})$ or $i > 30^{\circ}$
At the water-glass interface,
$μ_{'} = \frac{4}{3}, μ_{2} = 2$
$θ_{1} = θ = ?, θ_{2} = i = 30^{\circ}$
Since $μ_{1} {sin θ}_{1} = μ_{2} {sin θ}_{2},$ we get
$θ = {sin}^{- 1} [\frac{μ_{1}}{μ_{2}} {sin θ}_{1}]$
$\Rightarrow θ = {sin}^{- 1} (\frac{3}{4})$

Updated on:21/07/2023

Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle $θ$ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
A $\frac{4 π d}{λ} {(1 - \frac{1}{n^{2}} {sin}^{2} θ)}^{1 / 2} + π$
B $\frac{4 π d}{λ} {(1 - \frac{1}{n^{2}} {sin}^{2} θ)}^{1 / 2}$
C $\frac{4 π d}{λ} {(1 - \frac{1}{n^{2}} {sin}^{2} θ)}^{1 / 2} + \frac{π}{2}$
D $\frac{4 π d}{λ} {(1 - \frac{1}{n^{2}} {sin}^{2} θ)}^{1 / 2} + 2 π$