A ray of light falls on a transparent glass slab of refractive index 1.62. If the reflected ray and the refracted rays are mutually perpendicular, what is the angle of refraction ?
To solve the problem, we need to find the angle of refraction (R) when a ray of light falls on a transparent glass slab with a refractive index (μ) of 1.62, and the reflected ray and refracted ray are mutually perpendicular.
1. Understanding the Geometry:
- When the light ray strikes the glass slab, it is incident at an angle I.
- According to the law of reflection, the angle of reflection is also I.
- The angle between the reflected ray and the refracted ray is given to be 90 degrees.
2. Setting Up the Angles:
- If the angle of reflection is I, then the angle of refraction R can be expressed in terms of I since the reflected and refracted rays are perpendicular:
I+R=90∘
- Rearranging gives:
R=90∘−I
3. Applying Snell's Law:
- Snell's Law states that:
n1sinI=n2sinR
- Here, n1=1 (refractive index of air) and n2=1.62 (refractive index of glass).
- Substituting the values, we have:
1⋅sinI=1.62⋅sinR
4. Substituting for I:
- From the previous step, we know I=90∘−R.
- Therefore, we can substitute this into the equation:
sin(90∘−R)=1.62⋅sinR
- Using the identity sin(90∘−R)=cosR, we rewrite the equation:
cosR=1.62⋅sinR
5. Rearranging the Equation:
- Dividing both sides by sinR (assuming sinR≠0):
cotR=1.62
6. Finding the Angle R:
- To find R, we take the cotangent inverse:
R=cot−1(1.62)
- Using a calculator, we find:
R≈31.7∘
Final Answer:
The angle of refraction R is approximately 31.7∘.
- When the light ray strikes the glass slab, it is incident at an angle I.
- According to the law of reflection, the angle of reflection is also I.
- The angle between the reflected ray and the refracted ray is given to be 90 degrees.
- If the angle of reflection is I, then the angle of refraction R can be expressed in terms of I since the reflected and refracted rays are perpendicular:
I+R=90∘
- Rearranging gives:
R=90∘−I
- Snell's Law states that:
n1sinI=n2sinR
- Here, n1=1 (refractive index of air) and n2=1.62 (refractive index of glass).
- Substituting the values, we have:
1⋅sinI=1.62⋅sinR
- From the previous step, we know I=90∘−R.
- Therefore, we can substitute this into the equation:
sin(90∘−R)=1.62⋅sinR
- Using the identity sin(90∘−R)=cosR, we rewrite the equation:
cosR=1.62⋅sinR
- Dividing both sides by sinR (assuming sinR≠0):
cotR=1.62
- To find R, we take the cotangent inverse:
R=cot−1(1.62)
- Using a calculator, we find:
R≈31.7∘
The angle of refraction R is approximately 31.7∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A ray of light falls on a transparent glass slab of refractive index √2. If the reflected and refracted rays are mutually perpendicular, then the angle of incidence is
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

View Solution
Knowledge Check
A ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
A12B√32C32D√3
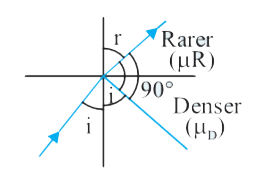
A ray of light is incident at an angle i from denser to rare medium. The reflected and the refracted rays are mutually perpendicular. The angle of reflection and the angle of refraction are respectively r and r'. Then the critical angle will be:
View SolutionA ray of light from a denser medium strikes a rarer medium at an angle of incidence i=tan−1(1/2). If the reflected and the refracted rays are mutually perpendicular to each-other, what is the value of the critical angle in degree?
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
View SolutionA : When an unpolarised light is incident on a glass plate at Brewster angle, the reflected ray and refracted ray are matually perpendicular.
R : The refractive index of glass is equal to sine of the angle of polarisation.
View SolutionWhen light is polarised by reflection from a transparent surface.
a) reflection and refracted rays are mutually perpendicular
b) both reflected and refracted rays are plane polarised
c) refraction ray is partially polarised
d) the R.I., of transparent surface is equal to tangent of Brewster.s angle
View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View Solution
