Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
4πdλ(1−1n2sin2θ)−1/2+π
4πdλ(1−1n2sin2θ)1/2
4πdλ(1−1n2sin2θ)1/2+π2
4πdλ(1−1n2sin2θ)1/2+2π
The correct Answer is:A
Consider the diagram the ray (P) is incident at an angle θ and gets reflected in the direction P and refracted in the direction P Due to reflection from the glass medium there is a phase change of π
Time taken to travel along OP
Δt=OPv=d/cosrc/n=ndccosr
From Snell's law n=sinθsinr⇒sinr=sinθn
cosr=√1−sin2r=√1−sin2θn2
∴Δt=ndc(1−sin2θn2)1/2=n2dc(1−sin2θn2)−1/2
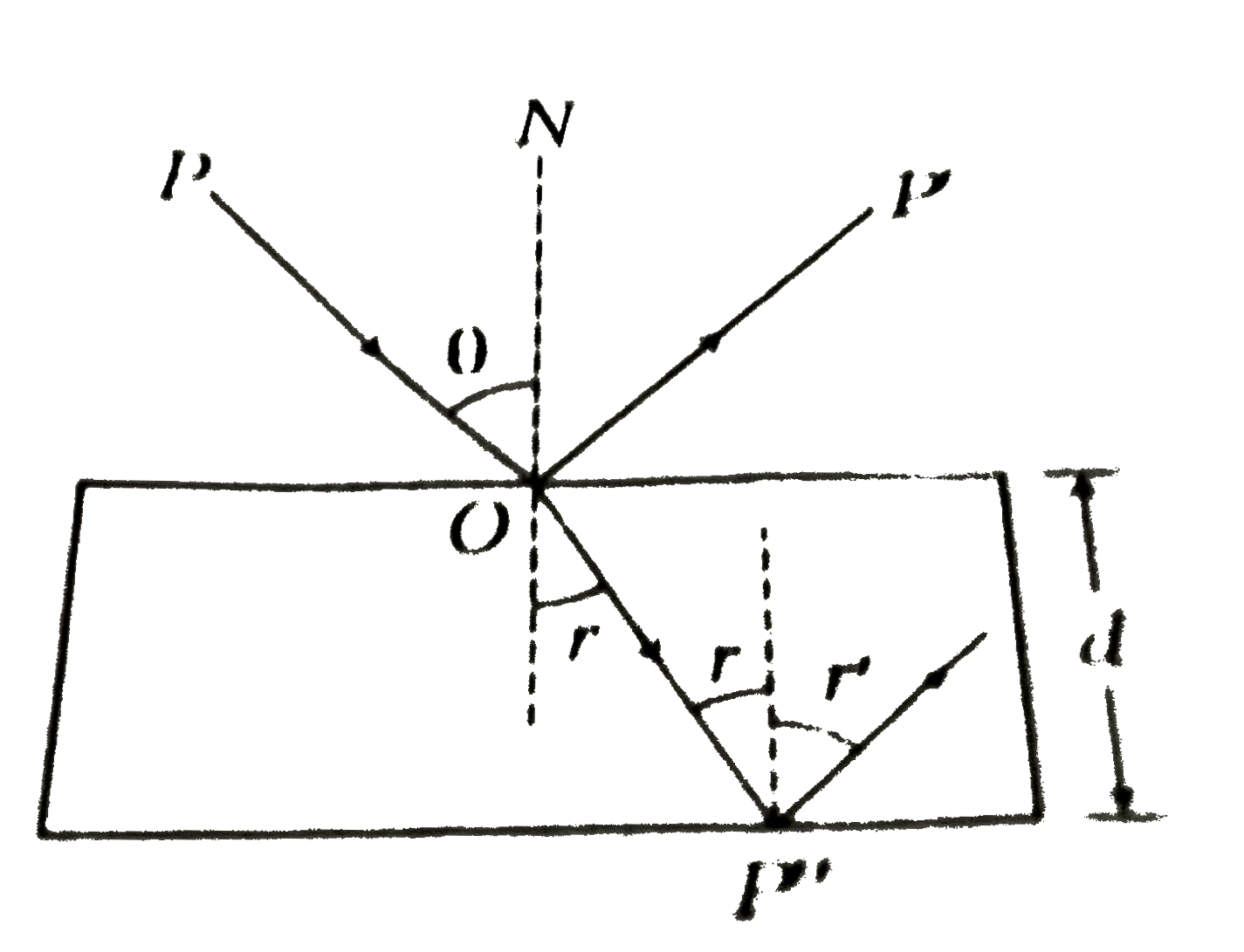
Phase difference =Δϕ=2πT×Δt=2πndλ(1−sin2θn2)−1/2
So, net phase difference =Δϕ+π=4πdλ(1−1n2sin2θ)−1/2+π
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason
8 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - match column
4 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Check point
65 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View Solution
Knowledge Check
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
A4πdλ(1−1n2sin2θ)1/2+πB4πdλ(1−1n2sin2θ)1/2C4πdλ(1−1n2sin2θ)1/2+π2D4πdλ(1−1n2sin2θ)1/2+2πA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
When a ray of light enters a glass slab from air
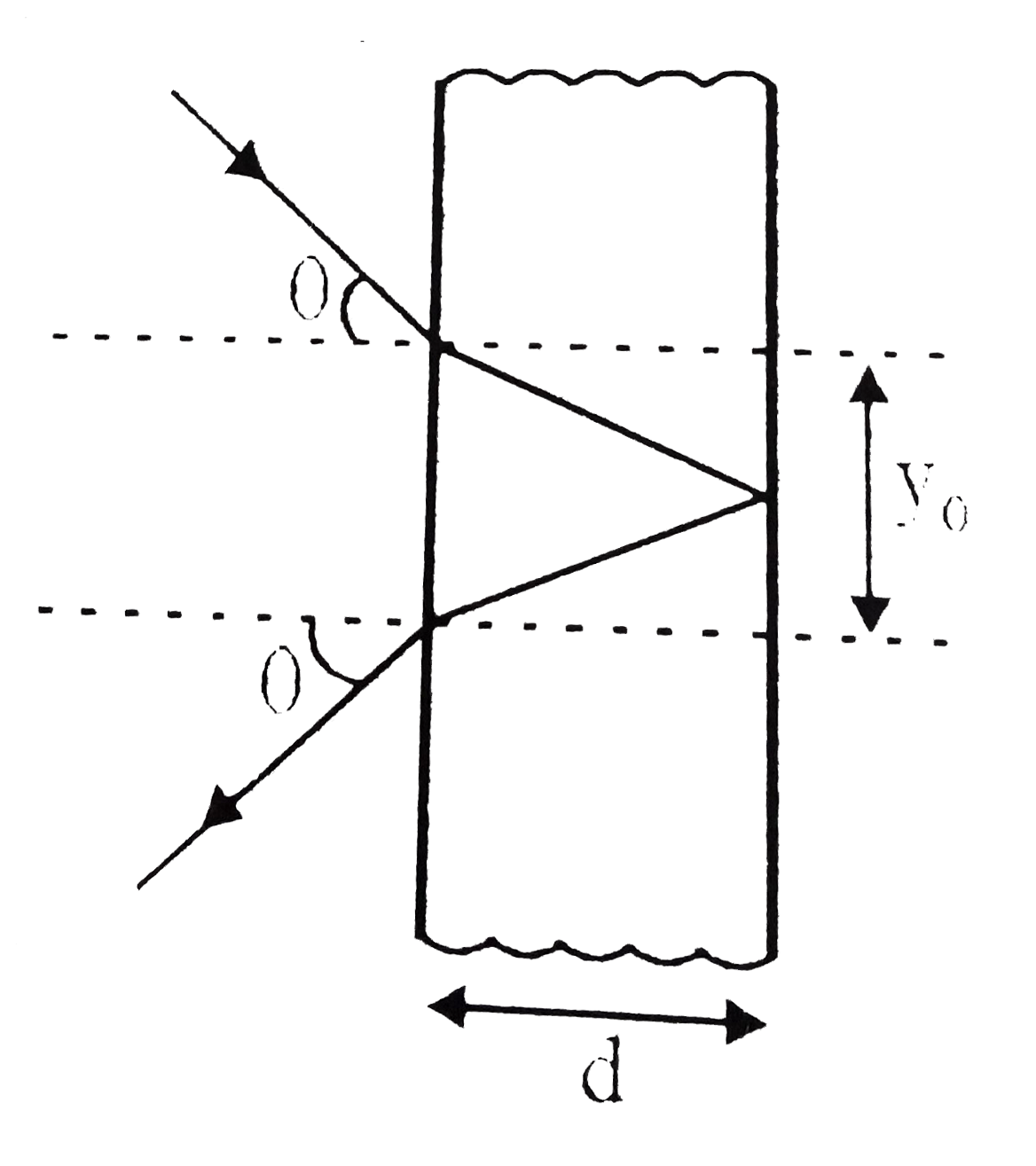
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
View SolutionWhen a ray of light enters a glass slab from air.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution
