The n transparent slabs of refractive index1.5 each having thickness 1cm, 2 cm,…to n cm are arranged one over another. A point object is seen through this combineation with near perpendicular light. If the shift of object by the combination is 1 cm, then find the value of n.
To solve the problem, we need to find the value of n given that n transparent slabs, each with a refractive index of 1.5 and thicknesses of 1 cm, 2 cm, ..., n cm, cause a shift of 1 cm when viewed through them.
1. Understanding the Shift Formula:
The shift Δx caused by a single slab of thickness t and refractive index μ is given by:
Δx=(1−1μ)t
For n slabs, the total shift Δxtotal can be expressed as:
Δxtotal=n∑i=1(1−1μ)ti
where ti is the thickness of the ith slab.
2. Calculating the Total Thickness:
The thicknesses of the slabs are 1 cm, 2 cm, ..., n cm. The sum of the thicknesses can be calculated using the formula for the sum of the first n natural numbers:
S=1+2+3+…+n=n(n+1)2
3. Substituting Values:
The refractive index μ is given as 1.5. Therefore, we can substitute this into our shift formula:
Δxtotal=(1−11.5)⋅S
Simplifying 1−11.5:
1−11.5=1−23=13
Thus, we have:
Δxtotal=13⋅n(n+1)2
4. Setting Up the Equation:
We know that the total shift Δxtotal is given as 1 cm:
1=13⋅n(n+1)2
Multiplying both sides by 3:
3=n(n+1)2
Multiplying both sides by 2:
6=n(n+1)
5. Forming a Quadratic Equation:
Rearranging gives us:
n2+n−6=0
6. Factoring the Quadratic:
We can factor this quadratic equation:
(n−2)(n+3)=0
This gives us two potential solutions:
n−2=0⇒n=2
n+3=0⇒n=−3
Since n must be a positive integer, we discard n=−3.
7. Final Answer:
Thus, the value of n is:
2
The shift Δx caused by a single slab of thickness t and refractive index μ is given by:
Δx=(1−1μ)t
For n slabs, the total shift Δxtotal can be expressed as:
Δxtotal=n∑i=1(1−1μ)ti
where ti is the thickness of the ith slab.
The thicknesses of the slabs are 1 cm, 2 cm, ..., n cm. The sum of the thicknesses can be calculated using the formula for the sum of the first n natural numbers:
S=1+2+3+…+n=n(n+1)2
The refractive index μ is given as 1.5. Therefore, we can substitute this into our shift formula:
Δxtotal=(1−11.5)⋅S
Simplifying 1−11.5:
1−11.5=1−23=13
Thus, we have:
Δxtotal=13⋅n(n+1)2
We know that the total shift Δxtotal is given as 1 cm:
1=13⋅n(n+1)2
Multiplying both sides by 3:
3=n(n+1)2
Multiplying both sides by 2:
6=n(n+1)
Rearranging gives us:
n2+n−6=0
We can factor this quadratic equation:
(n−2)(n+3)=0
This gives us two potential solutions:
n−2=0⇒n=2
n+3=0⇒n=−3
Since n must be a positive integer, we discard n=−3.
Thus, the value of n is:
2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.4
12 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.2
20 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
k transparent slabs are arranged one over another. The refractive indices of the slabs are g„ ...Ilk and the thicknesses are t1,t2,t3.............,tk . An object is seen through this combination with nearly perpendicular light. Find the equivalent refractive index of the system which will allow the image to be formed at the same place.
View Solution
If the distance between two images formed by upper and lower part of the lens of the point object placed at 30 cm from given lens is 11n (in cm) then find n:
View SolutionA glass slab of thickness 3cm and refractive index 1.5 is placed in front of a concave mirror of focal length 20cm. Where should a point object be placed if it is to image on to itself?
View SolutionFour transparent slabs having thickness t1=2cm,t2=4cm,t3=3cm and t4=5cm are introduced in one of the paths of light emitted by two narrow slits the ascending order of shift of the central fringe
View SolutionThere is a spherical glass shell of refractive index 1.5, inner radius 10 cm and outer radius 20 cm. Inside th espherical cavity, there is air. A point object is placed at a point O at a distance of 30cm from the outer spherical surface. Find the final position of th eimage as seen eye.

View SolutionA 20cm thick glass slab of refractive index 1.5 is kept in front of a plane mirror. Find the position of the image (relative to mirror) as seen by an observer through the glass slab when a point object is kept in air at a distance of 40cm from the mirror.
View SolutionAn object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slabe of thickness 3cm and refractive index 1.5 is then placed close to the irror in the space between the object and the mirror. The distance of the near surface of the slabe from the mirror is 1cm. The final image from the mirror will be formed at
View SolutionA slab of glass of refractive index 1.5 and thickness 3cm is placed with the faces perpendicular to the principle axis of a concave mirror. If the radius of curvature of the mirror is 10cm, the distance at which an object must be placed from the mirror so that the image coincides with the object is
View SolutionIn a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
View SolutionA parallel beam of light is incident on a lens of focal length 10cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The nature of the final image from the lens slab combination is: (Assume rays paraxial)
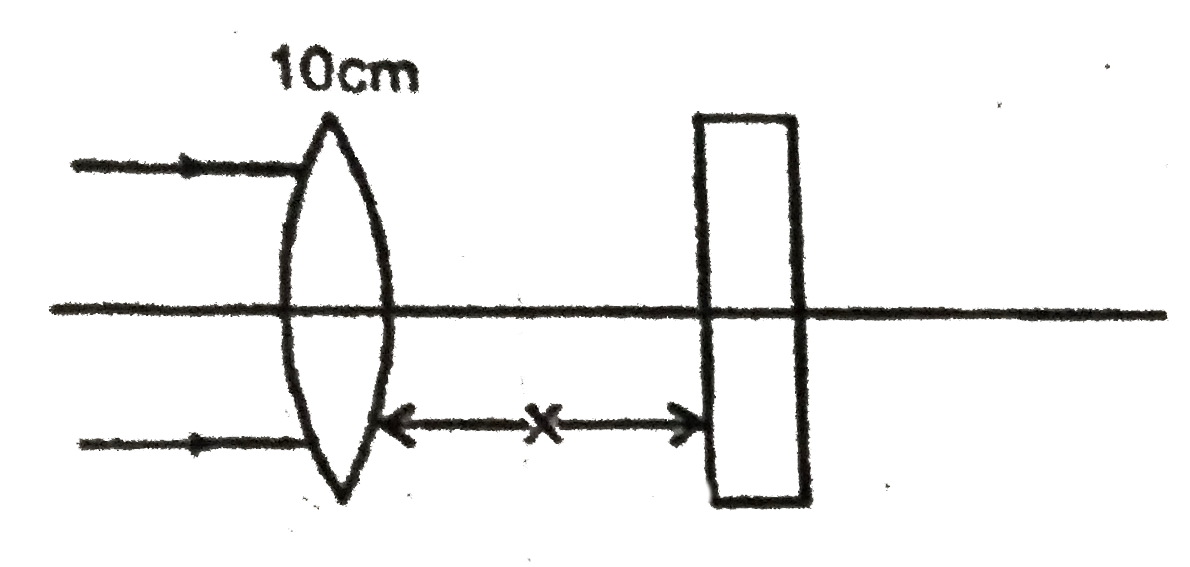
View Solution
