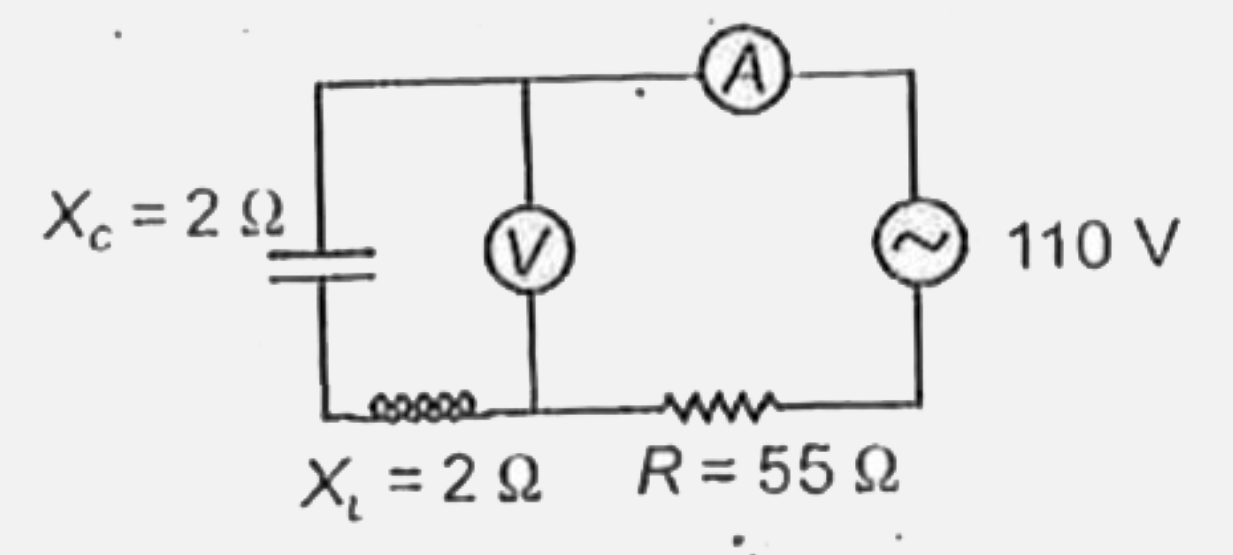
In the above question, the reading of ammeter is 40xA. What is the value of x?
The correct Answer is:(3)
To find the value of x in the ammeter reading given as 40x A, we can follow these steps:
Step 1: Understand the Circuit
The circuit consists of resistances and a battery. We have a 10 V battery, a 10 ohm internal resistance, and two resistors of 4 ohm and 5 ohm. The current I splits into two branches, one with current I1 through the 5 ohm resistor and the other with current I−I1 through the 4 ohm resistor.
Step 2: Apply Kirchhoff's Loop Law
We will apply Kirchhoff's loop law to the two loops in the circuit.
Loop 1:
Starting from the 5 ohm resistor:
5I1−10+I⋅1=0
This simplifies to:
5I1+I=10(Equation 1)
Loop 2:
Starting from the 4 ohm resistor:
5I1−4(I−I1)=0
Expanding this gives:
5I1−4I+4I1=0
Combining like terms results in:
9I1−4I=0(Equation 2)
Step 3: Solve the Equations
From Equation 1, we can express I:
I=10−5I1
Substituting I into Equation 2:
9I1−4(10−5I1)=0
Expanding this gives:
9I1−40+20I1=0
Combining terms results in:
29I1=40
Thus, we find:
I1=4029 A
Step 4: Relate to the Ammeter Reading
The ammeter reading is given as 40x A. Since we have found I1=4029 A, we can set these equal:
40x=4029
Step 5: Solve for x
Cross-multiplying gives:
40⋅29=40⋅x
Dividing both sides by 40 results in:
x=29
Conclusion
The value of x is 29.
---
The circuit consists of resistances and a battery. We have a 10 V battery, a 10 ohm internal resistance, and two resistors of 4 ohm and 5 ohm. The current I splits into two branches, one with current I1 through the 5 ohm resistor and the other with current I−I1 through the 4 ohm resistor.
We will apply Kirchhoff's loop law to the two loops in the circuit.
Starting from the 5 ohm resistor:
5I1−10+I⋅1=0
This simplifies to:
5I1+I=10(Equation 1)
Starting from the 4 ohm resistor:
5I1−4(I−I1)=0
Expanding this gives:
5I1−4I+4I1=0
Combining like terms results in:
9I1−4I=0(Equation 2)
From Equation 1, we can express I:
I=10−5I1
9I1−4(10−5I1)=0
Expanding this gives:
9I1−40+20I1=0
Combining terms results in:
29I1=40
Thus, we find:
I1=4029 A
The ammeter reading is given as 40x A. Since we have found I1=4029 A, we can set these equal:
40x=4029
Cross-multiplying gives:
40⋅29=40⋅x
Dividing both sides by 40 results in:
x=29
The value of x is 29.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Comprehansion
Explore 15 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:compression type
Explore 7 Videos
Similar Questions
Knowledge Check
The reading of ammeter shown in figure is
 A6.56AB3.28AC2.18AD1.09A
A6.56AB3.28AC2.18AD1.09A
In the figure above, x∣∣y. What is the value of a?Ab+cB2b-cC180-b+cD180-b-c

In the figure above, what is the value of x?
View Solution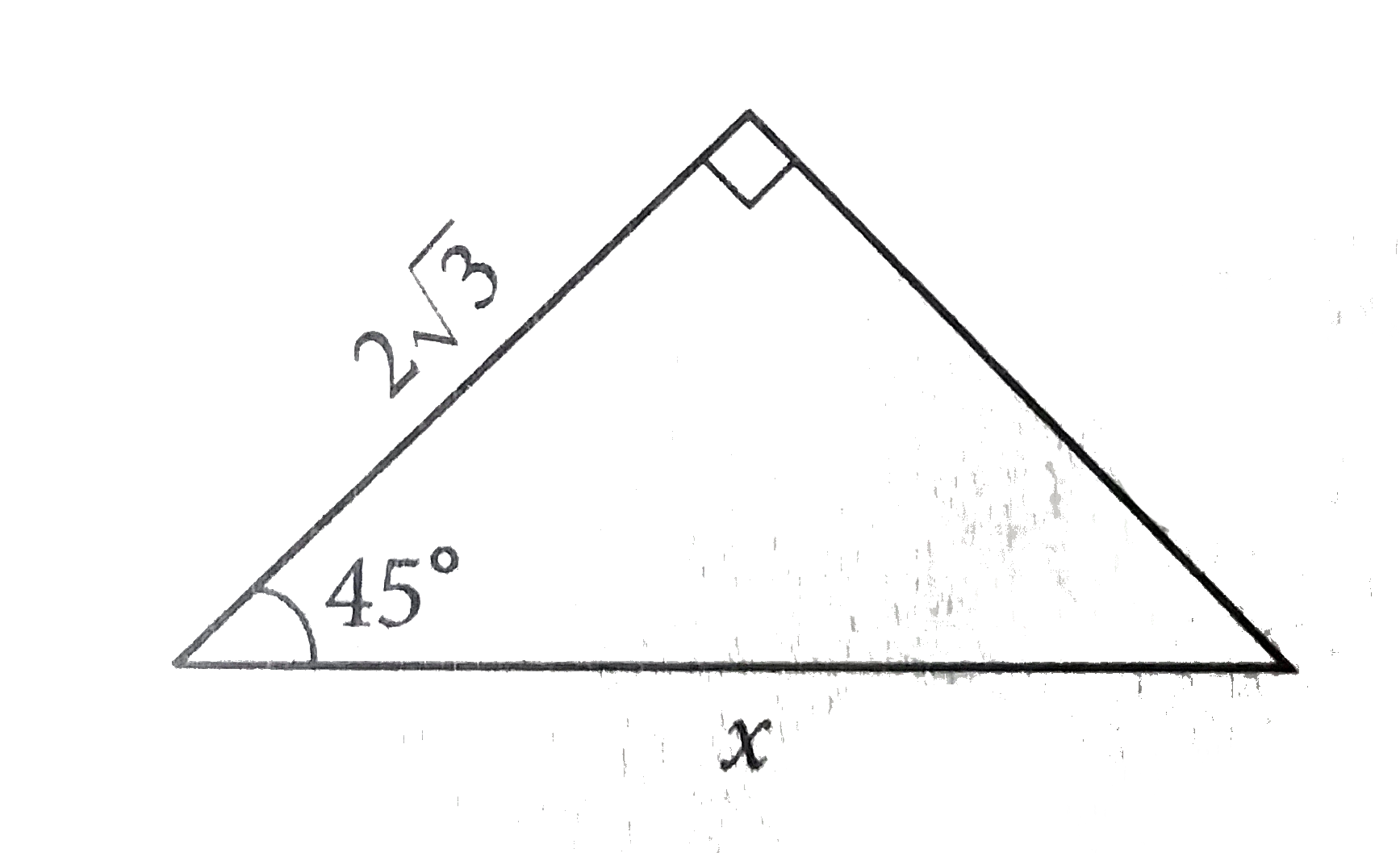
In the figure above, what is the value of x?
View Solution
In the figure above, what is the value of x?
View Solution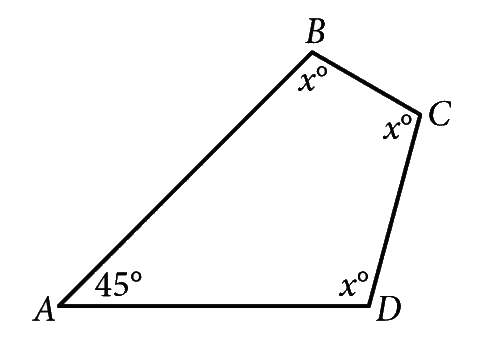
In the figure above, what is the value of x ?
View Solution
On the number above. What is the value of point x?
View Solution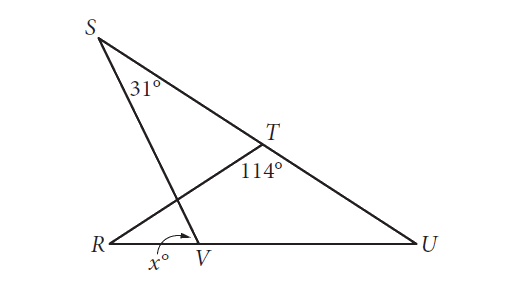
In the figure above, RT = TU.What is the value of x ?
View Solution