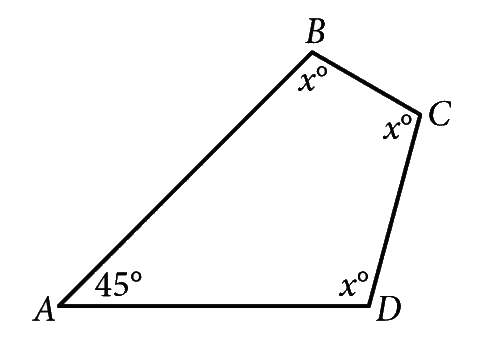
In the figure above, what is the value of x ?
A
45
B
90
C
100
D
105
Video Solution
Text Solution
The correct Answer is:D
The figure is a quadrilateral, so the sum of the measures of its interior angles is 360∘. The value of x can be found by using the equation 45 + 3x = 360. Subtracting 45 from both sides of the equation results in 3x = 315, and dividing both sides of the resulting equation by 3 yields x = 105. Therefore, the value of x in the figure is 105. Choice A is incorrect. If the value of x were 45, the sum of the measures of the angles in the figure would be 45 + 3(45), or 180∘, but the sum of the measures of the angles in a quadrilateral is 360∘. Choice B is incorrect. If the value of x were 90, the sum of the measures of the angles in the figure would be 45 + 3(90), or 315∘, but the sum of the measures of the angles in a quadrilateral is 360∘. Choice C is incorrect. If the value of x were 100, the sum of the measures of the angles in the figure would be 45 + 3(100), or 345∘, but the sum of the measures of the angles in a quadrilateral is 360∘.
|
Similar Questions
Knowledge Check

In the figure above , what is the value of a?A40B60C100D130
In the figure above, what is the value of y?A20B30C45D60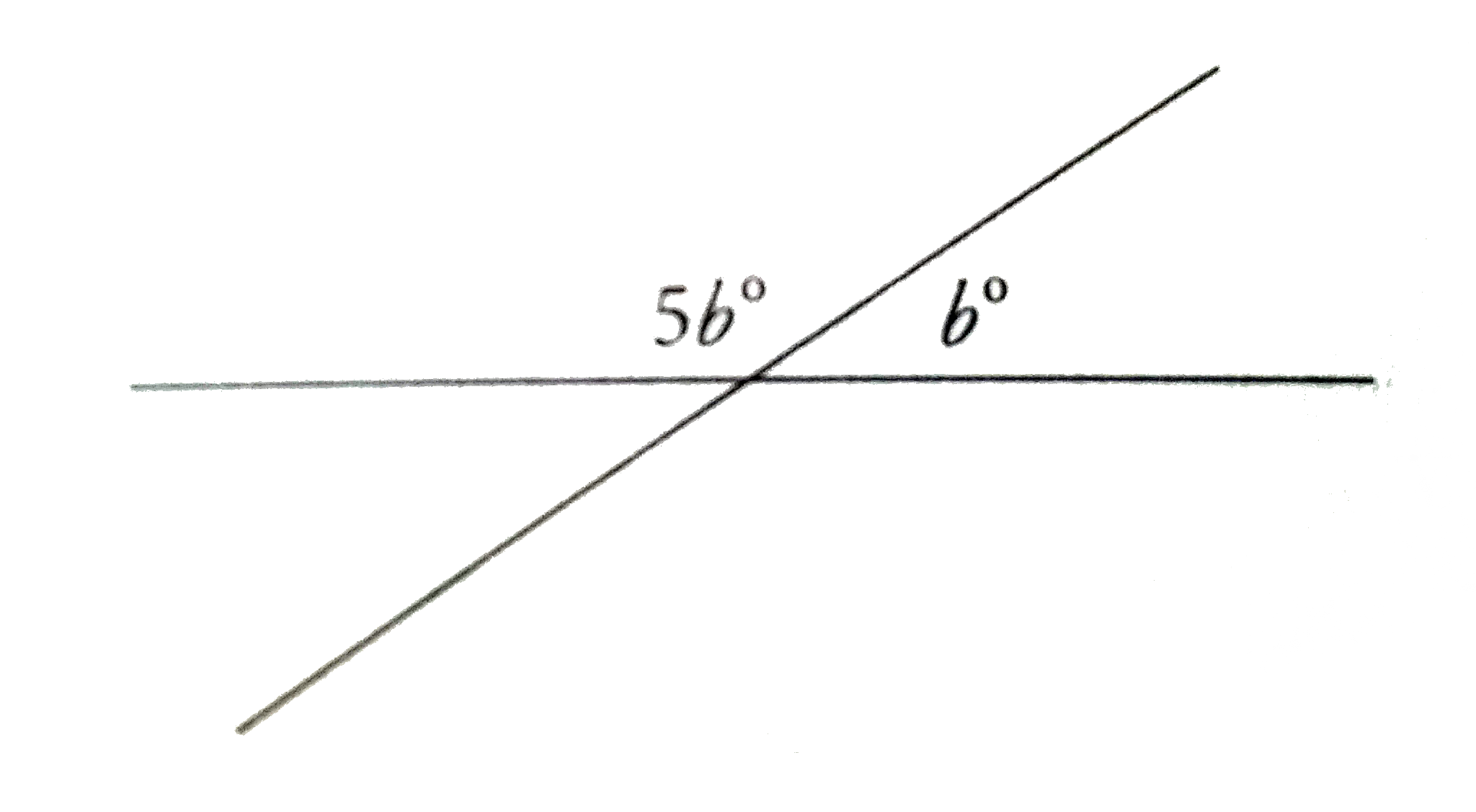
In the figure above, what is the value of b?A20∘B30∘C40∘D45∘

In the figure above what is the value of p+q?
View Solution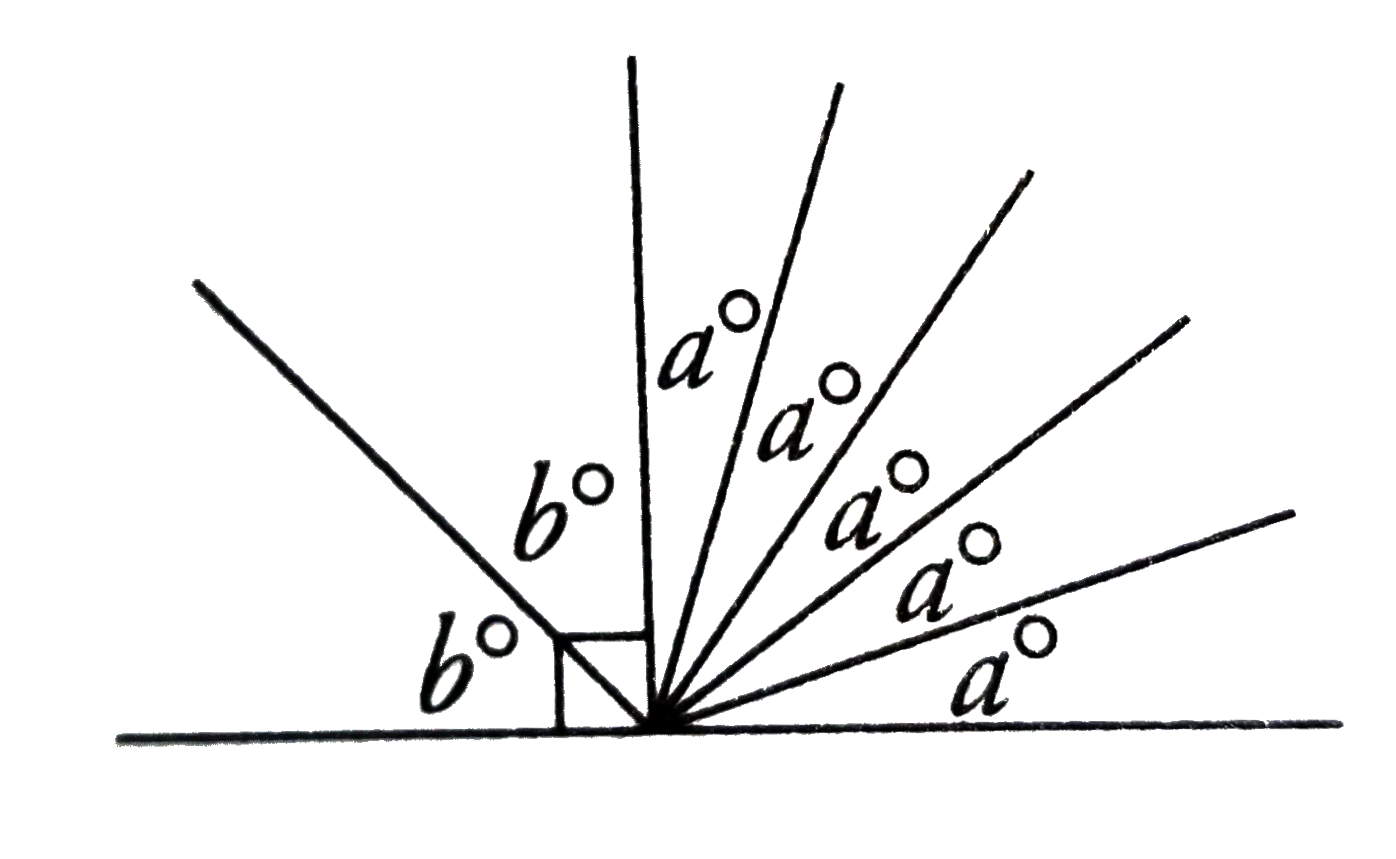
In the figure above, what is the value of 4a-b?
View Solution
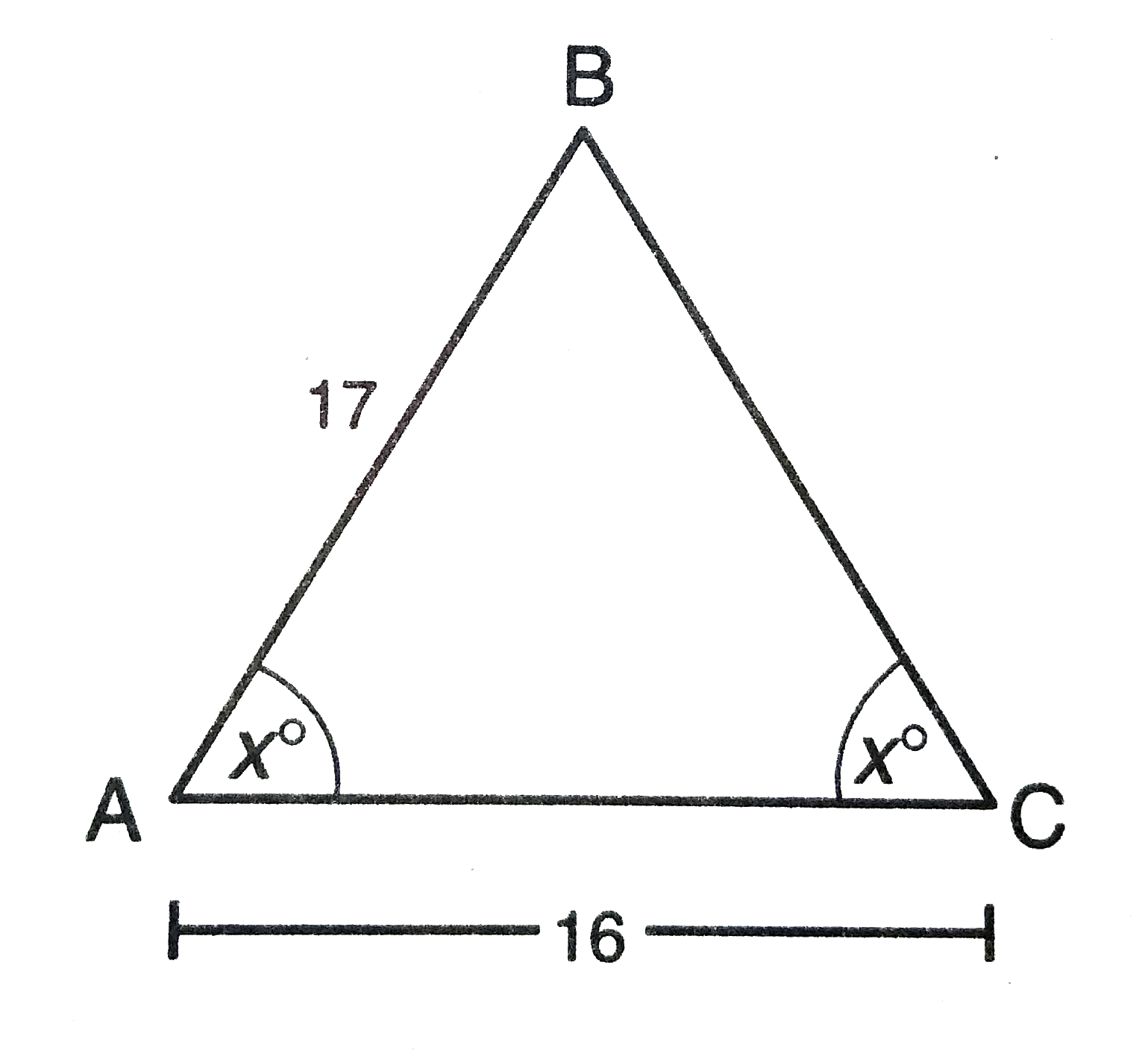
In the figure above, x=
View Solution
In the figure above, what is the value of cosa∘ if cos(90∘−a∘)=35?
View Solution
In the figure above, what is the value of h(0)−3(g(1)−f(2)) ?
View Solution