A 5m potentiometer wire having 3Ω resistance per meter is connected to a storage cell of steady emf 2V and internal resistance 1Ω. A primary cell is balanced against 3.5m of it. When a resistance of 32/nΩ is put in series with the storage cell, the null point shifts to the centre of the last wire, i.e., 4.5m. What is 'n'?
The correct Answer is:(7)
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
Step 1: Calculate the total resistance of the potentiometer wire
The potentiometer wire has a length of 5 m and a resistance of 3 Ω per meter.
Total resistance of the wire=Length×Resistance per meter=5m×3Ω/m=15Ω
Hint: Remember that the total resistance of a wire is the product of its length and resistance per unit length.
Step 2: Calculate the total resistance in the circuit
The circuit includes the resistance of the potentiometer wire and the internal resistance of the storage cell.
Total resistance=Resistance of wire+Internal resistance=15Ω+1Ω=16Ω
Hint: When calculating total resistance in a series circuit, simply add the individual resistances.
Step 3: Calculate the current flowing through the circuit
Using Ohm's law, we can find the current (I) flowing through the circuit with the given emf (E) of 2 V.
I=ETotal resistance=2V16Ω=18A
Hint: Ohm's law states that current is equal to voltage divided by resistance.
Step 4: Calculate the potential gradient (K)
The potential gradient (K) is defined as the potential difference per unit length.
K=VL=I⋅RL
Substituting the values:
K=(1/8)⋅15Ω5m=15/85=38V/m
Hint: The potential gradient can be calculated using the current and the total resistance of the wire divided by its length.
Step 5: Calculate the potential difference (E_p) across 3.5 m of the potentiometer wire
The potential difference across a length of wire can be calculated using the potential gradient.
Ep=K⋅L1=38V/m⋅3.5m=3⋅3.58=10.58=2116V
Hint: To find the potential difference across a certain length, multiply the potential gradient by that length.
Step 6: Set up the equation for the new null point
When a resistance of 32nΩ is added in series, the total resistance becomes 16+32n. The new null point is at 4.5 m.
The new potential difference across 4.5 m of the wire is:
Ep=K⋅4.5=38⋅4.5=13.58V
Hint: The new potential difference can be found similarly to the previous step, using the new length and the same potential gradient.
Step 7: Relate the potential differences
The potential difference across the new null point must equal the potential difference across the total resistance:
2116=I1⋅(15+32n)
Where I1 is the current through the wire after adding the resistance.
Step 8: Calculate the new current (I_1)
The new current can be expressed as:
I1=216+32n=2n16n+32
Step 9: Substitute and solve for n
Substituting I1 into the equation:
2116=2n16n+32⋅(15+32n)
Cross-multiplying and simplifying will yield the value of n.
After solving, we find:
n=7
Final Answer
The value of n is 7.
---
The potentiometer wire has a length of 5 m and a resistance of 3 Ω per meter.
The circuit includes the resistance of the potentiometer wire and the internal resistance of the storage cell.
Using Ohm's law, we can find the current (I) flowing through the circuit with the given emf (E) of 2 V.
The potential gradient (K) is defined as the potential difference per unit length.
The potential difference across a length of wire can be calculated using the potential gradient.
When a resistance of 32nΩ is added in series, the total resistance becomes 16+32n. The new null point is at 4.5 m.
The potential difference across the new null point must equal the potential difference across the total resistance:
The new current can be expressed as:
Substituting I1 into the equation:
The value of n is 7.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Comprehansion
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
A potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of emf 2 volt and internal resistance 1Ω. If a cell of emf 1.2 volt is balanced by it, the balancing length will be
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionThe resistance of 0.1 N solution of acetic acid is 250 ohm whne measured ina cell of cell constant 250 ohm whne measured in acell of cell constant 1.15 cm−1 The equivalent conductance (inohm−1cm2equivalent−1) of 0.1 N acetic acid is
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
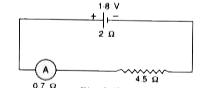
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View Solution
