A potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
The correct Answer is:(5)
To solve the problem step by step, we will use the information provided about the potentiometer wire, the battery, and the external resistance.
1. Understand the Given Data:
- Length of the potentiometer wire, L=10m
- Resistance of the potentiometer wire, Rw=30Ω
- EMF of the battery, E=2.5V
- Internal resistance of the battery, ri=5Ω
- Fall of potential along the potentiometer wire, K=50μV/mm=50×10−6V/mm=50×10−6×10−3V/m=50×10−9V/m
2. Calculate the Total Resistance in the Circuit:
The total resistance Rtotal in the circuit is given by:
Rtotal=Rw+ri+R
where R is the external resistance we need to find.
3. Calculate the Current in the Circuit:
The current I flowing through the circuit can be calculated using Ohm's law:
I=ERtotal=ERw+ri+R
4. Relate the Potential Gradient to the Voltage:
The potential gradient K is defined as:
K=VL
where V is the potential difference across the potentiometer wire. Thus,
V=K⋅L
5. Express the Voltage in Terms of Current:
The voltage across the potentiometer wire can also be expressed as:
V=I⋅Rw
6. Set Up the Equation:
Equating the two expressions for V:
K⋅L=I⋅Rw
Substituting I from step 3:
K⋅L=(ERw+ri+R)⋅Rw
7. Substitute Known Values:
Substitute the known values into the equation:
50×10−9⋅10=(2.530+5+R)⋅30
Simplifying gives:
5×10−8=7535+R
8. Cross Multiply and Solve for R:
Cross multiplying gives:
5×10−8(35+R)=75
Expanding and rearranging:
5×10−8R=75−5×10−8⋅35
Calculate 5×10−8⋅35:
5×10−8⋅35=1.75×10−6
Thus:
5×10−8R=75−1.75×10−6
5×10−8R=75−0.00000175≈75
Therefore:
R≈755×10−8=1.5×109Ω
9. Convert R to the Form 23nΩ:
Given R=23nΩ, we have:
1.5×109=23×10n
Solving for n:
n=9−1=8
Final Answer:
The value of n is 5.
- Length of the potentiometer wire, L=10m
- Resistance of the potentiometer wire, Rw=30Ω
- EMF of the battery, E=2.5V
- Internal resistance of the battery, ri=5Ω
- Fall of potential along the potentiometer wire, K=50μV/mm=50×10−6V/mm=50×10−6×10−3V/m=50×10−9V/m
The total resistance Rtotal in the circuit is given by:
Rtotal=Rw+ri+R
where R is the external resistance we need to find.
The current I flowing through the circuit can be calculated using Ohm's law:
I=ERtotal=ERw+ri+R
The potential gradient K is defined as:
K=VL
where V is the potential difference across the potentiometer wire. Thus,
V=K⋅L
The voltage across the potentiometer wire can also be expressed as:
V=I⋅Rw
Equating the two expressions for V:
K⋅L=I⋅Rw
Substituting I from step 3:
K⋅L=(ERw+ri+R)⋅Rw
Substitute the known values into the equation:
50×10−9⋅10=(2.530+5+R)⋅30
Simplifying gives:
5×10−8=7535+R
Cross multiplying gives:
5×10−8(35+R)=75
Expanding and rearranging:
5×10−8R=75−5×10−8⋅35
Calculate 5×10−8⋅35:
5×10−8⋅35=1.75×10−6
Thus:
5×10−8R=75−1.75×10−6
5×10−8R=75−0.00000175≈75
Therefore:
R≈755×10−8=1.5×109Ω
Given R=23nΩ, we have:
1.5×109=23×10n
Solving for n:
n=9−1=8
The value of n is 5.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Comprehansion
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
A potentiometer wire of length 10m and resistance 30 ohm is connected in series with a battery of emf 2.5V, internal resistance 5 ohm and external resistance R. If the fall of potential along the potentiometer wire is 50mV/m, the value of R is ohms is
View SolutionA potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
View SolutionA potentiometer wire of Length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f. E will be given by :
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
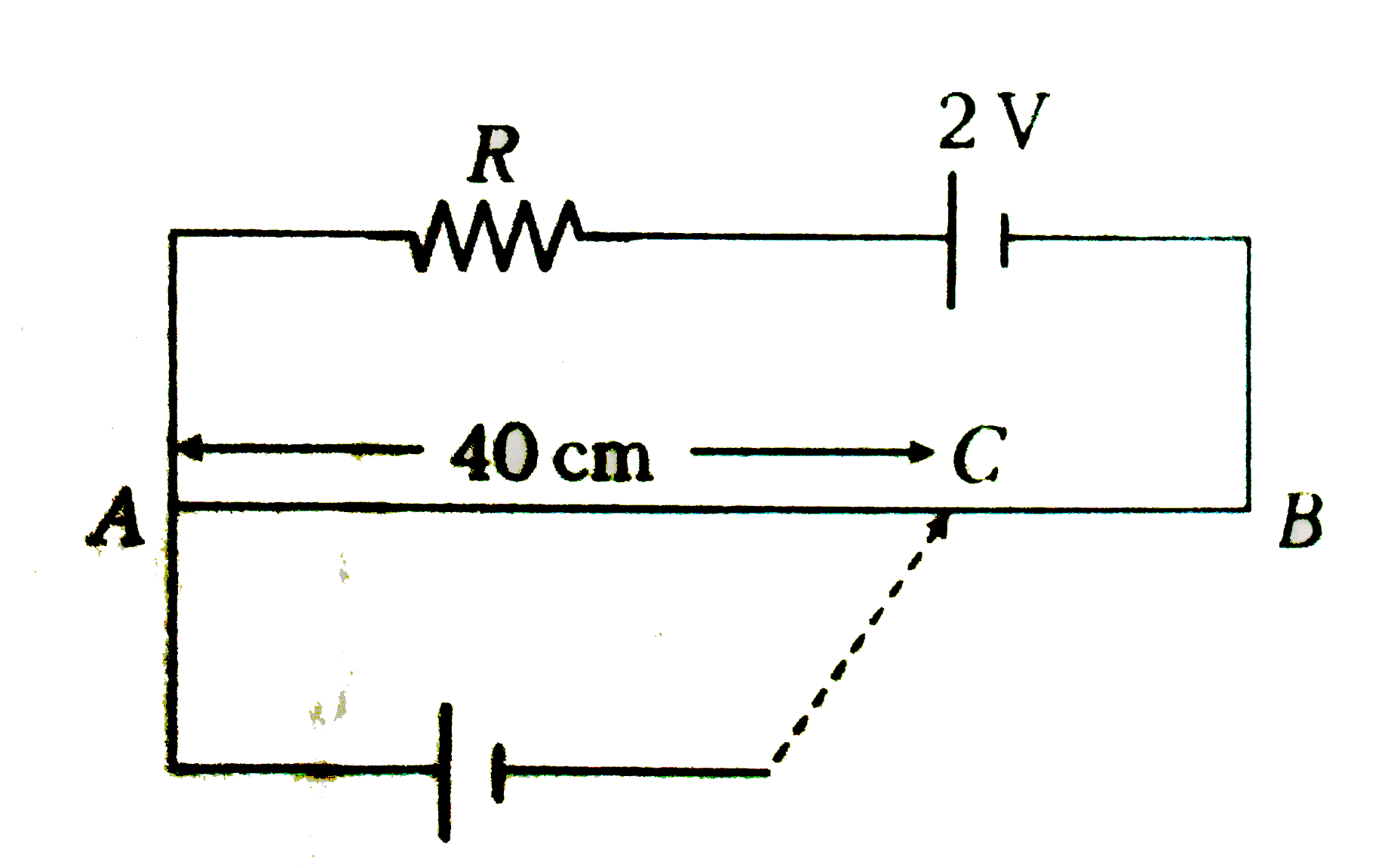
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
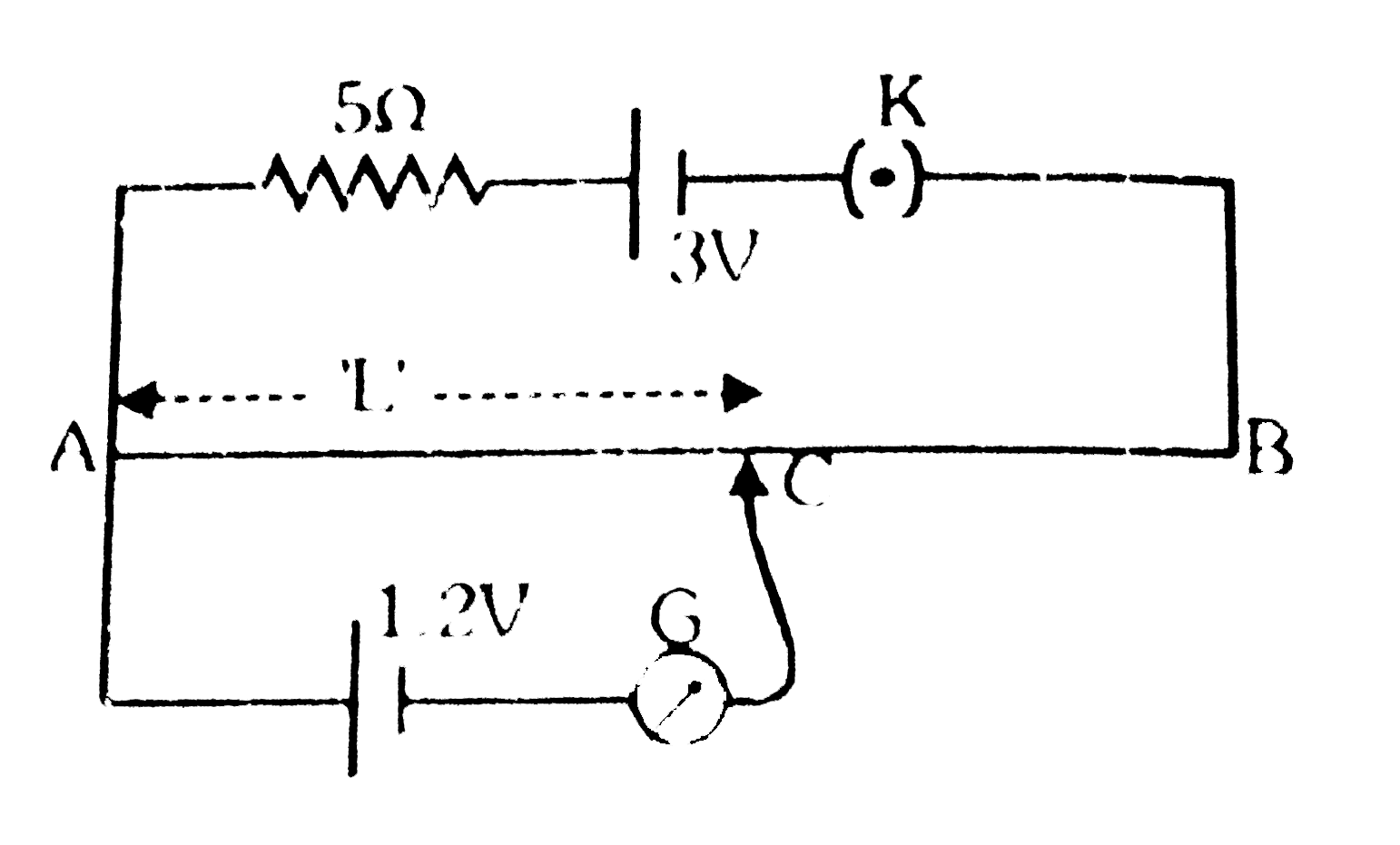
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View Solution
