An electric dipole consists of two opposite charges each of magnitude 1 mC separated by 2 cm. The dipole is placed in an external uniform field of 105NC−1 intensity. Find the
a. maximum torque exterted by the field on the dipole, and
b. work done in roating the dipole through 180∘ starting from the position θ=0∘.
To solve the problem step by step, we will break it down into two parts: (a) finding the maximum torque exerted by the field on the dipole, and (b) calculating the work done in rotating the dipole through 180 degrees.
Part (a): Maximum Torque
1. Identify the given values:
- Charge (q) = 1 mC = 1×10−3 C
- Separation distance (2a) = 2 cm = 2×10−2 m
- External electric field (E) = 105 N/C
2. Calculate the dipole moment (p):
The dipole moment p is given by the formula:
p=q×d
where d is the separation distance between the charges. Since the charges are separated by 2a, we have:
d=2a=2×10−2 m
Thus,
p=(1×10−3 C)×(2×10−2 m)=2×10−5 C m
3. Determine the maximum torque (τ):
The torque τ exerted on a dipole in an electric field is given by:
τ=p⋅E⋅sinθ
The maximum torque occurs when θ=90∘ (i.e., sin90∘=1):
τmax=p⋅E
Substituting the values:
τmax=(2×10−5 C m)⋅(105 N/C)=2 N m
Part (b): Work Done in Rotating the Dipole
1. Work done (W) in rotating the dipole:
The work done in rotating the dipole from an angle θ1 to θ2 is given by:
W=∫θ2θ1τdθ
Here, we need to calculate the work done from θ=0∘ to θ=180∘.
2. Substituting the expression for torque:
W=∫180∘0p⋅E⋅sinθdθ
3. Integrate the expression:
The integral of sinθ is:
∫sinθdθ=−cosθ
Therefore,
W=p⋅E(−cosθ)180∘0
Evaluating the limits:
W=p⋅E(−cos(180∘)+cos(0∘))
Since cos(180∘)=−1 and cos(0∘)=1:
W=p⋅E(−(−1)+1)=p⋅E⋅2
4. Substituting the values:
W=2⋅(2×10−5 C m)⋅(105 N/C)=4 J
Final Answers:
- (a) Maximum Torque = 2 N m
- (b) Work Done = 4 J
- Charge (q) = 1 mC = 1×10−3 C
- Separation distance (2a) = 2 cm = 2×10−2 m
- External electric field (E) = 105 N/C
The dipole moment p is given by the formula:
p=q×d
where d is the separation distance between the charges. Since the charges are separated by 2a, we have:
d=2a=2×10−2 m
Thus,
p=(1×10−3 C)×(2×10−2 m)=2×10−5 C m
The torque τ exerted on a dipole in an electric field is given by:
τ=p⋅E⋅sinθ
The maximum torque occurs when θ=90∘ (i.e., sin90∘=1):
τmax=p⋅E
Substituting the values:
τmax=(2×10−5 C m)⋅(105 N/C)=2 N m
The work done in rotating the dipole from an angle θ1 to θ2 is given by:
W=∫θ2θ1τdθ
Here, we need to calculate the work done from θ=0∘ to θ=180∘.
W=∫180∘0p⋅E⋅sinθdθ
The integral of sinθ is:
∫sinθdθ=−cosθ
Therefore,
W=p⋅E(−cosθ)180∘0
Evaluating the limits:
W=p⋅E(−cos(180∘)+cos(0∘))
Since cos(180∘)=−1 and cos(0∘)=1:
W=p⋅E(−(−1)+1)=p⋅E⋅2
W=2⋅(2×10−5 C m)⋅(105 N/C)=4 J
- (a) Maximum Torque = 2 N m
- (b) Work Done = 4 J
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.2
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
An electric dipole consists of two opposite charges each of magnitude 2 μC separated by a distance 1 cm. The dipole is placed in an external field of 103 N/C. The maximum torque on the dipole is
View SolutionAn electric dipole consists of two opposite charges of magnitude 1/3×10−7C, separated by 2 cm. The dipole is placed in an external field of 3×107NC−1. What maximum torque does the electrc field exert on the dipole ?
View SolutionAn electric dipole consists of two opposite charges of magnitude 1μC separated by a distance of 2cm.The dipole is placed in an electric filled 10−5Vm−1.The maximum torque that the field exert on the dipole is
View SolutionAn electric dipole consists of two charges of 0.1μC separated bu a distance of 2.0cm. The dipole is placed in an external field of 105NC−1. What maximum torqur does the field exert on the dipole?
View SolutionAn electric dipole consisting of two opposite charges of 2×10−6C each separated by a distance of 3cm is placed in an electirc field of 2×105N/C. The maximum torque on the dipole is will be
View SolutionTwo opposite and equal chrages 4×10−8 coulomb when placed 2×10−2cm away, from a dipole. If dipole is placed in an external electric field 4×108 newton/coulomb, the value of maximum torque and the work done in rotating it through 180∘ will be
View SolutionAn electric dipole made up of a positive and negative charge, each of 1μC separated by a distance of 2cm is placed in an electric field of 105N/C, then the work done in rotating the dipole from the position of stable equilibrium through an angle of 180∘ is
View SolutionTwo point charges of 3.2×10−19Cand−3.2×10−19C are separated from each other by 2.4×10−10m. The dipole is situated in a uniform electric field of intensity 4×105Vm−1. Calculate the work done in roating the dipole by 180∘.
View SolutionAn electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
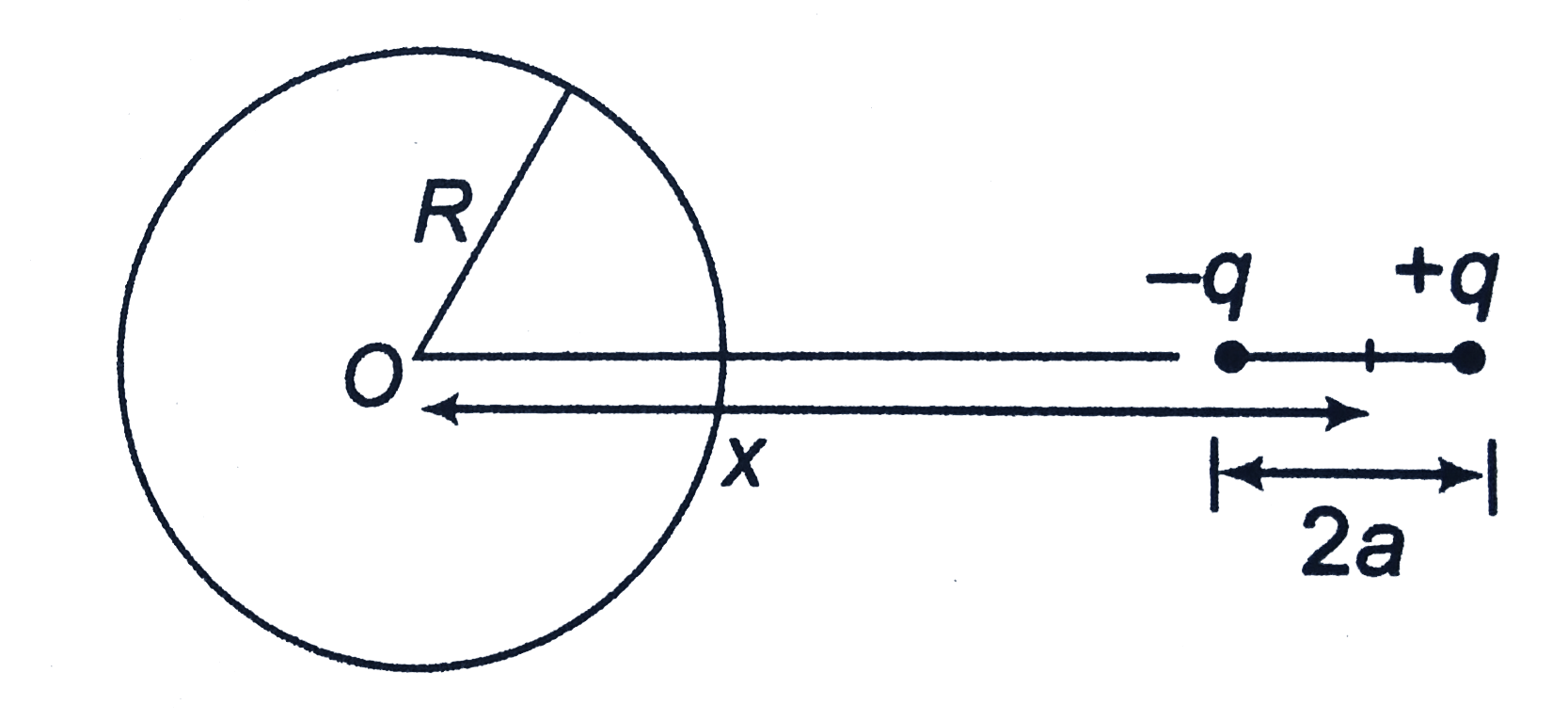
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?
View SolutionTwo point-charges +2eand−2e are situated at a distance of 2.4Å from each other and constitude an electric dipole. This dipole is placed in a uniform electric field of 4.0×105Vm−1. Calculate
(i) electric dipole moment,
(ii) potential energy of the dipole in equilibrium position,
(iii) work done in rotating the dipole through 180∘ from the equilibrium position.
View Solution
