An electric dipole consists of two opposite charges of magnitude 1/3×10−7C, separated by 2 cm. The dipole is placed in an external field of 3×107NC−1. What maximum torque does the electrc field exert on the dipole ?
To find the maximum torque exerted on an electric dipole in an external electric field, we can follow these steps:
Step 1: Understand the parameters of the dipole
Given:
- Magnitude of each charge, q=13×10−7C
- Separation distance, d=2cm=0.02m
- External electric field, E=3×107N/C
Step 2: Calculate the dipole moment p
The dipole moment p is given by the formula:
p=q⋅d
Substituting the values:
p=(13×10−7C)×(0.02m)
Calculating this gives:
p=13×10−7×0.02=23×10−9C⋅m
Step 3: Calculate the maximum torque τmax
The maximum torque τmax on the dipole in an electric field is given by:
τmax=p⋅E
Substituting the values we calculated:
τmax=(23×10−9C⋅m)×(3×107N/C)
Calculating this gives:
τmax=23×10−9×3×107=2×10−2N⋅m
Final Answer
The maximum torque exerted on the dipole is:
τmax=0.02N⋅m
Given:
- Magnitude of each charge, q=13×10−7C
- Separation distance, d=2cm=0.02m
- External electric field, E=3×107N/C
The dipole moment p is given by the formula:
p=q⋅d
Substituting the values:
p=(13×10−7C)×(0.02m)
Calculating this gives:
p=13×10−7×0.02=23×10−9C⋅m
The maximum torque τmax on the dipole in an electric field is given by:
τmax=p⋅E
Substituting the values we calculated:
τmax=(23×10−9C⋅m)×(3×107N/C)
Calculating this gives:
τmax=23×10−9×3×107=2×10−2N⋅m
The maximum torque exerted on the dipole is:
τmax=0.02N⋅m
Similar Questions
An electric dipole consists of two opposite charges each of magnitude 2 μC separated by a distance 1 cm. The dipole is placed in an external field of 103 N/C. The maximum torque on the dipole is
View SolutionAn electric dipole consists of two opposite charges each of magnitude 1 mC separated by 2 cm. The dipole is placed in an external uniform field of 105NC−1 intensity. Find the
a. maximum torque exterted by the field on the dipole, and
b. work done in roating the dipole through 180∘ starting from the position θ=0∘.
View SolutionAn electric dipole consists of two charges of 0.1μC separated bu a distance of 2.0cm. The dipole is placed in an external field of 105NC−1. What maximum torqur does the field exert on the dipole?
View SolutionAn electric dipole consists of two opposite charges of magnitude 1μC separated by a distance of 2cm.The dipole is placed in an electric filled 10−5Vm−1.The maximum torque that the field exert on the dipole is
View SolutionAn electric dipole consisting of two opposite charges of 2×10−6C each separated by a distance of 3cm is placed in an electirc field of 2×105N/C. The maximum torque on the dipole is will be
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
View SolutionAn electric dipole made up of a positive and negative charge, each of 1μC separated by a distance of 2cm is placed in an electric field of 105N/C, then the work done in rotating the dipole from the position of stable equilibrium through an angle of 180∘ is
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
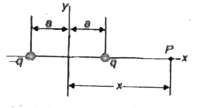
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionA neutral water molecule (H2O) in its vapour state has an electric dipole moment of magnitude 6.2×10−30cm.
a. How far apart are the molecules' centers of positive and negative charge ?
b. If a molecule is placed in an electric field of 1.5×104NC−1, what maximum torque can the field exert on it ? (Such a field can easily be set up in the laboratory).
c. How much work must an external agent do to turn this molecule end for end in this field, starting from its fully aligned position, for which θ=0 ?
View SolutionThe force experienced by a charge of 2μC in an electric field is 3×10−3N. The intensity of the electric field.
View Solution