The potential energies associated with four orientations of an electric dipole in an electric field are (1)−5U0,(2)−7U0,(3)3U0,and(4)5U0, where U0 is positive. Rank the orientation according to the angle between the electric dipole moment →P and the electric field →E, and B magnitude of the torque on the electric dipole, greatest first.
To solve the problem, we need to analyze the potential energies associated with the orientations of the electric dipole in the electric field. The potential energy U of an electric dipole in an electric field is given by the formula:
U=−→P⋅→E=−PEcosθ
where:
- →P is the electric dipole moment,
- →E is the electric field,
- θ is the angle between →P and →E.
Given the potential energies:
1. U1=−5U0
2. U2=−7U0
3. U3=3U0
4. U4=5U0
Step 1: Determine the angles θ
For the negative potential energies:
- For U1=−5U0:
−PEcosθ1=−5U0⟹PEcosθ1=5U0⟹cosθ1=5U0PE
- For U2=−7U0:
−PEcosθ2=−7U0⟹PEcosθ2=7U0⟹cosθ2=7U0PE
For the positive potential energies:
- For U3=3U0:
−PEcosθ3=3U0⟹PEcosθ3=−3U0⟹cosθ3=−3U0PE
- For U4=5U0:
−PEcosθ4=5U0⟹PEcosθ4=−5U0⟹cosθ4=−5U0PE
Step 2: Analyze the angles
Since PE is a constant, we can rank the angles based on the values of cosθ:
- For U1 and U2 (negative potential energies), the angles θ1 and θ2 are acute since cosθ is positive.
- For U3 and U4 (positive potential energies), the angles θ3 and θ4 are obtuse since cosθ is negative.
Step 3: Ranking the angles
- Since U2 has the largest magnitude of negative potential energy, θ2 will be the smallest angle.
- U1 has a smaller magnitude than U2, so θ1 will be larger than θ2.
- U3 has a smaller magnitude than U4, so θ3 will be larger than θ4.
Thus, we can rank the angles as follows:
1. θ2<θ1<θ4<θ3
Step 4: Determine the torque
The torque τ on the dipole is given by:
τ=PEsinθ
- The torque will be maximum for angles where sinθ is maximum. This occurs when θ is 90 degrees (for angles in the first and second quadrants).
- Since θ3 and θ4 are obtuse, they will have lower torque compared to θ1 and θ2.
Step 5: Ranking the torque
- τ3 will be the maximum since it corresponds to the smallest angle.
- τ1 and τ4 will be equal since they correspond to the same magnitude of potential energy.
- τ2 will be the least.
Thus, we can rank the torque as follows:
1. τ3>τ1=τ4>τ2
Final Rankings
- Angles: θ2<θ1<θ4<θ3
- Torque: τ3>τ1=τ4>τ2
- →P is the electric dipole moment,
- →E is the electric field,
- θ is the angle between →P and →E.
1. U1=−5U0
2. U2=−7U0
3. U3=3U0
4. U4=5U0
- For U1=−5U0:
−PEcosθ1=−5U0⟹PEcosθ1=5U0⟹cosθ1=5U0PE
- For U2=−7U0:
−PEcosθ2=−7U0⟹PEcosθ2=7U0⟹cosθ2=7U0PE
- For U3=3U0:
−PEcosθ3=3U0⟹PEcosθ3=−3U0⟹cosθ3=−3U0PE
−PEcosθ4=5U0⟹PEcosθ4=−5U0⟹cosθ4=−5U0PE
- For U3 and U4 (positive potential energies), the angles θ3 and θ4 are obtuse since cosθ is negative.
- U1 has a smaller magnitude than U2, so θ1 will be larger than θ2.
- U3 has a smaller magnitude than U4, so θ3 will be larger than θ4.
1. θ2<θ1<θ4<θ3
τ=PEsinθ
- Since θ3 and θ4 are obtuse, they will have lower torque compared to θ1 and θ2.
- τ1 and τ4 will be equal since they correspond to the same magnitude of potential energy.
- τ2 will be the least.
1. τ3>τ1=τ4>τ2
- Torque: τ3>τ1=τ4>τ2
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.2
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
The torque acting on an electric dipole of moment p held at an angle θ with an electric field E is ………. .
View SolutionA dipole of dipole moment →P is placed in uniform electric field →E, then torque acting on it is given by
View Solution(Fig. 3.95) shows four orientations of an electric dipole in an external electric field. Rank the orientations acording to the
a. magnitude of the torque on the dipole, and
b. potential energy of the dipole, greatest first.
 .
.
View SolutionAn electric dipole of moment →P is lying along a uniform electric field →E. The work done in rotating the dipole by 90∘ is:
View SolutionObtain the expression for the torque →τ experienced by an electric dipole of dipole moment →p in a uniform electric field , →E
View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View SolutionAn electric dipole is placed in a uniform electric field →E of magnitude 40N/C. Graph shows the magnitude of the square on the dipole versus the angle θ between the field →E and the dipole moment →p. The magnitude of dipole moment →p is equal to:
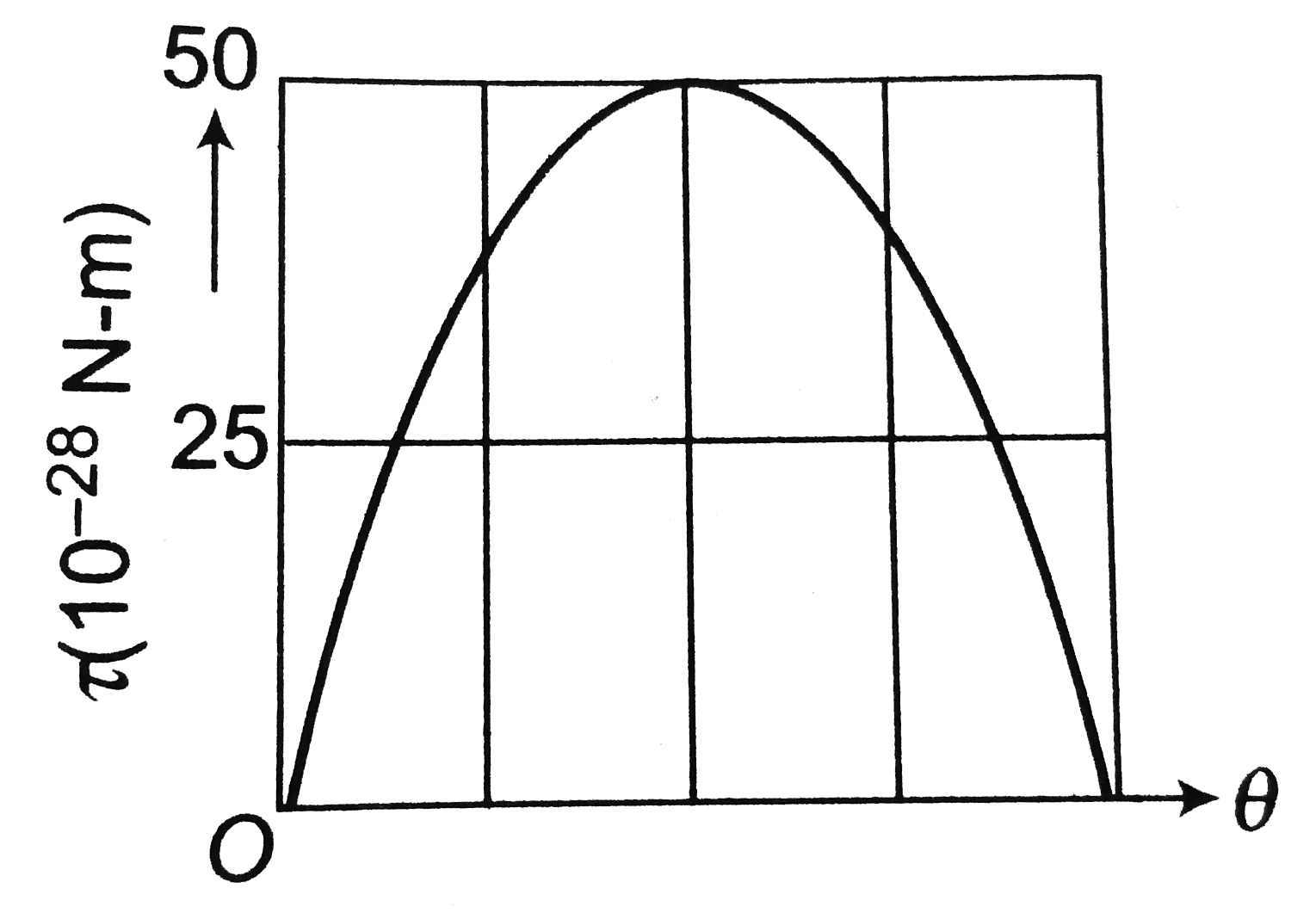
View SolutionAn electric dipole when placed in uniform electric field has zero potential energy. The angle between dipole moment and electric field is ....
View SolutionAn electric dipole when placed in uniform electric field has zero potential energy. The angle between dipole moment and electric field is ....
View SolutionA dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive direction of p and E, then the potential energy of the electric dipole is largest when θ is
View Solution
