A small sphere of mass m=0.5kg carrying a positive charge q=110μC is connected with a light, flexible, and inextensible string of length of length r=60cm and whirled in a vertical circle. If a vertically upward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
Weight mg(=0.5×10=5N) of sphere acts vertically downward and electric force q.E(=110×10−6×105=11N) vertically upward
Since upward force q E is greater than downward force mg, critical condition corresponds to the tension in the thread to be zero at lowest point A of the circle instead of highest point B,
Let velocity at lowest point be v0. Considering free body diagram of sphere at A.
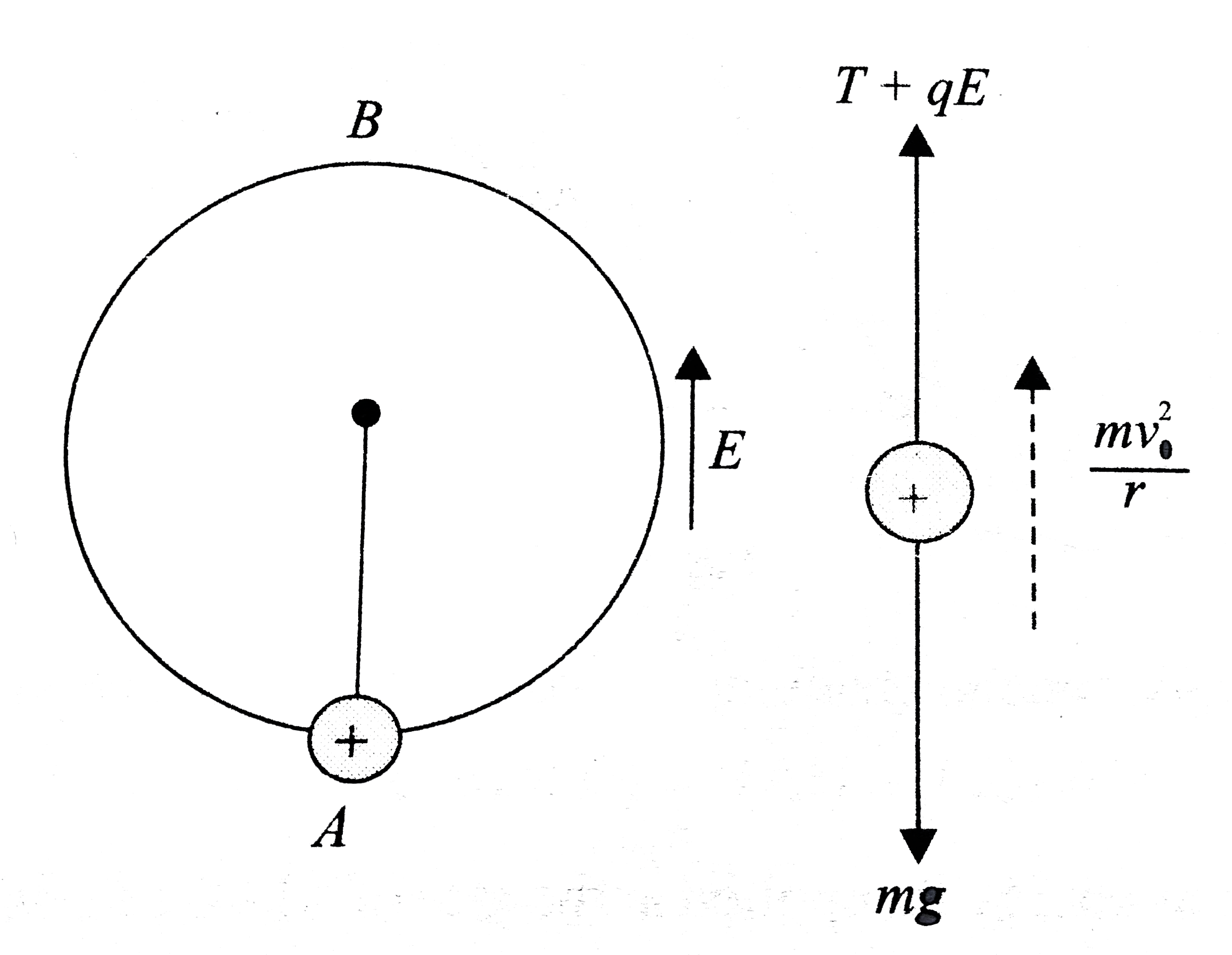 .
.
T+qE−mg=mv20r where T=0 or v0=6√5ms−1
But corresponding velocity at highest point is to be calculated. As sphere moves from A to B, work is done on it by electric field. Due to this work, both kinetic energy and gravitational potential energy of sphere increase. Hence, according to law of conservation of energy, minimum required velocity v at highest point is given by
12mv2=12mv20+qE.2r−mg.2r or v=6ms−1.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.39videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective28videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.123videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A small sphere of mass m=0.6kg carrying a positive charge q=80μC is connected with a light, flexible, and inextensible string of length r=30cm and whirled in a vertical circle. If a horizontal rightward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View SolutionTwo small particles A and B having masses m=0.5kg each and charges q1=(−155/18μC) and q2=(+100μC), respectively, are connected at the ends of a nonconducting, flexible, and inextensible string of length r=0.5m.
Particle A is fixed and B is whirled along a vertical circle with center at A. if a vertically upward electric field of Strength E=1.1×105NC−1 exists in the space, calculate the minimum velocity of particle B required at the highest point so that it may just complete the circle (g=10ms−2).
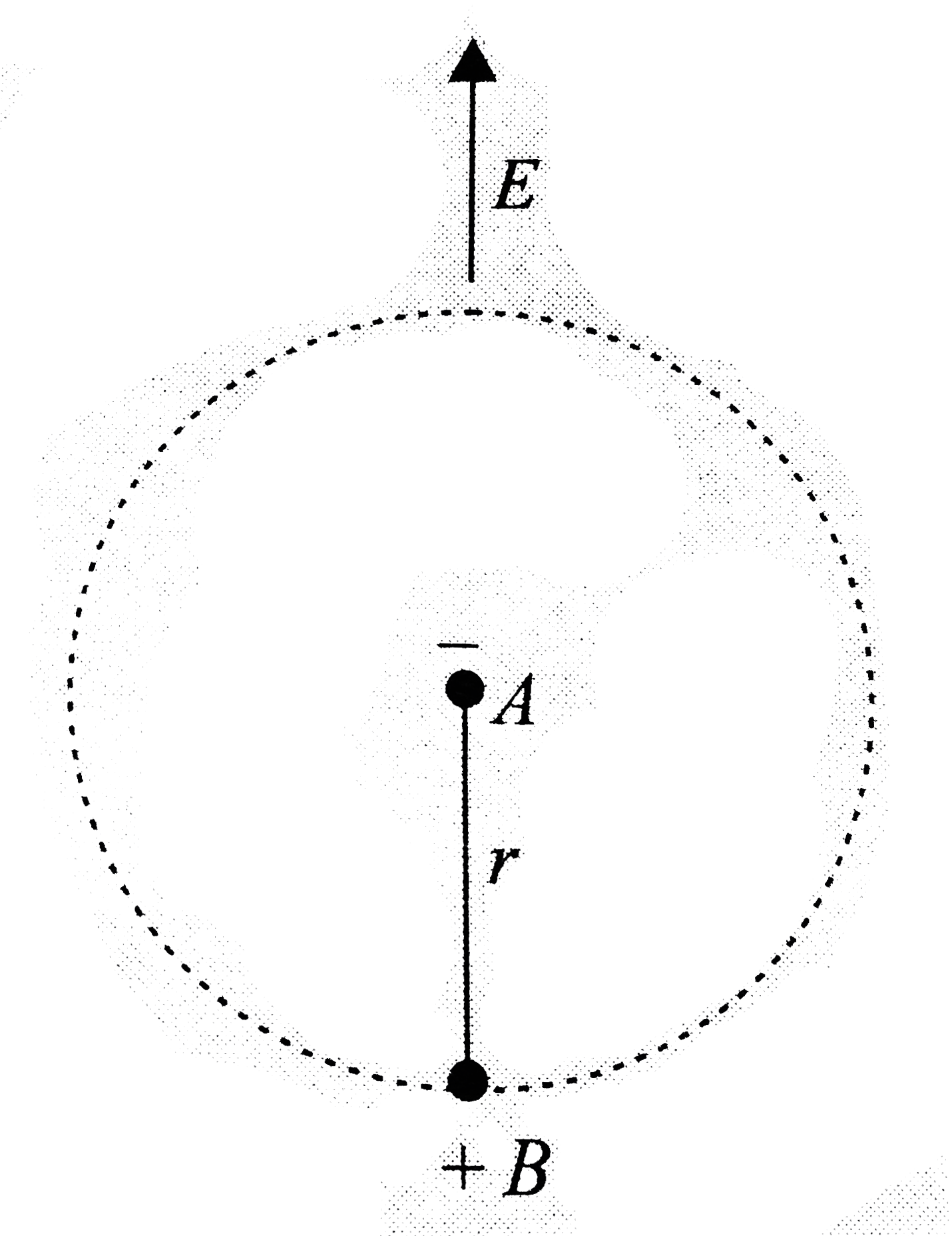 .View Solution
.View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View SolutionOne end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
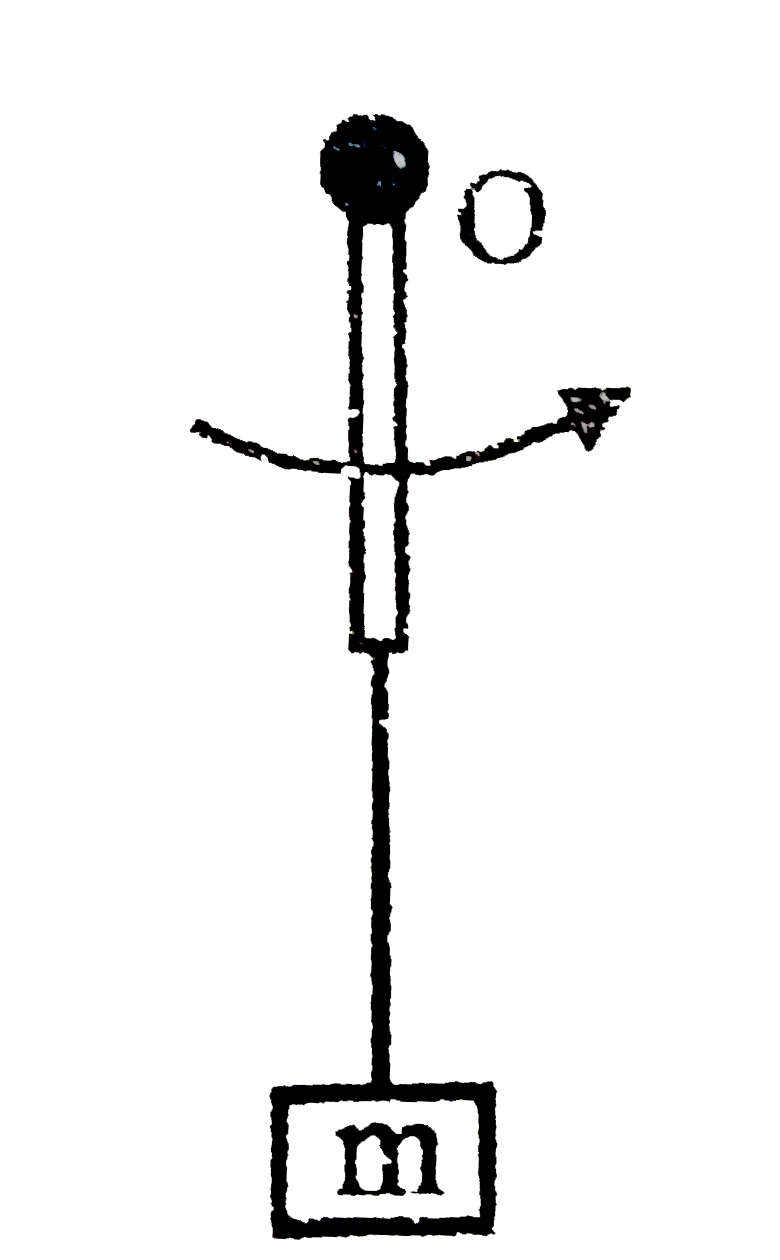 View Solution
View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
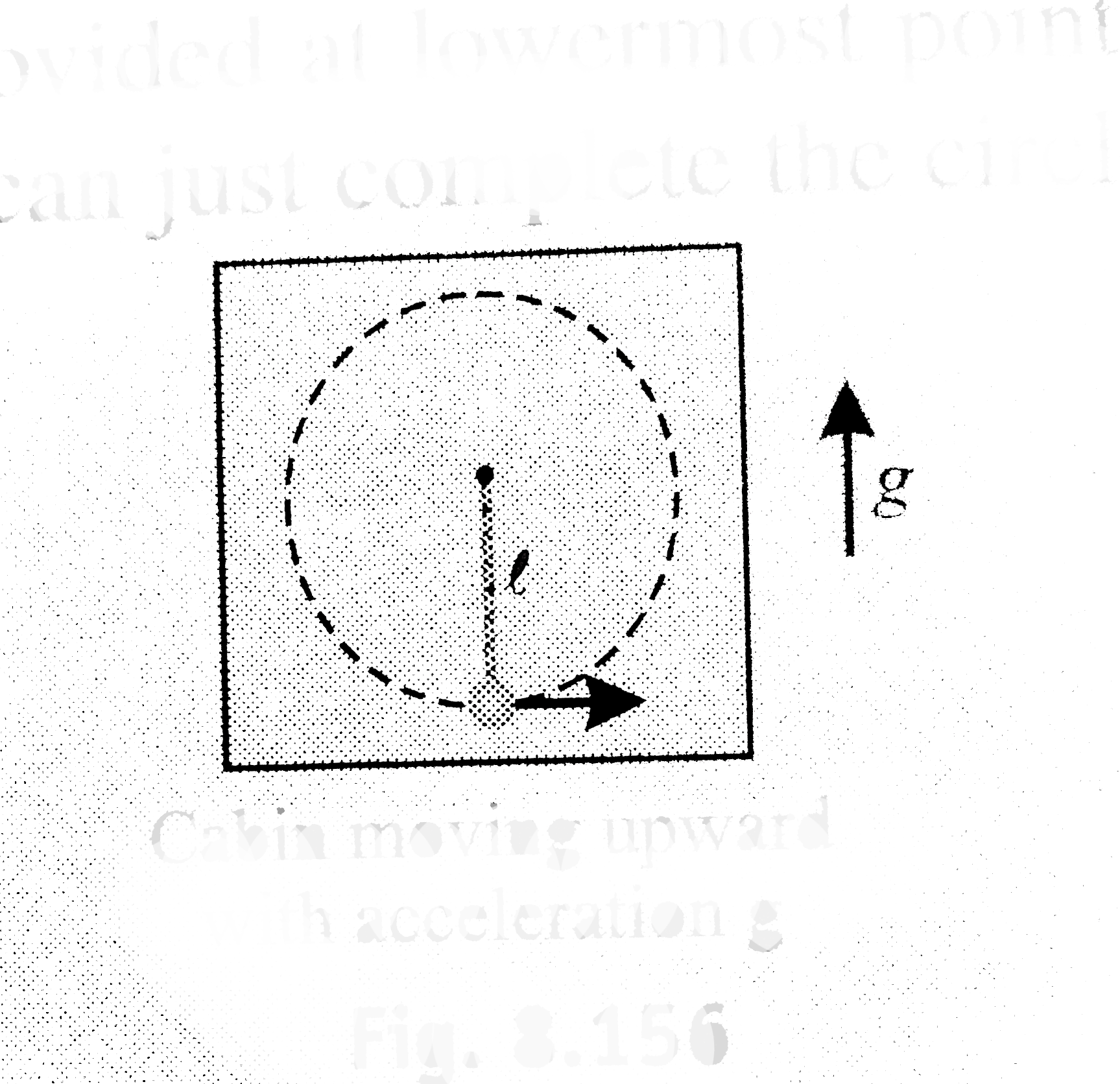 View Solution
View SolutionA small particle of mass m attached with a light inextensible thread of length L is moving in a vertical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Kinetic energy of the particle at the lower most position is
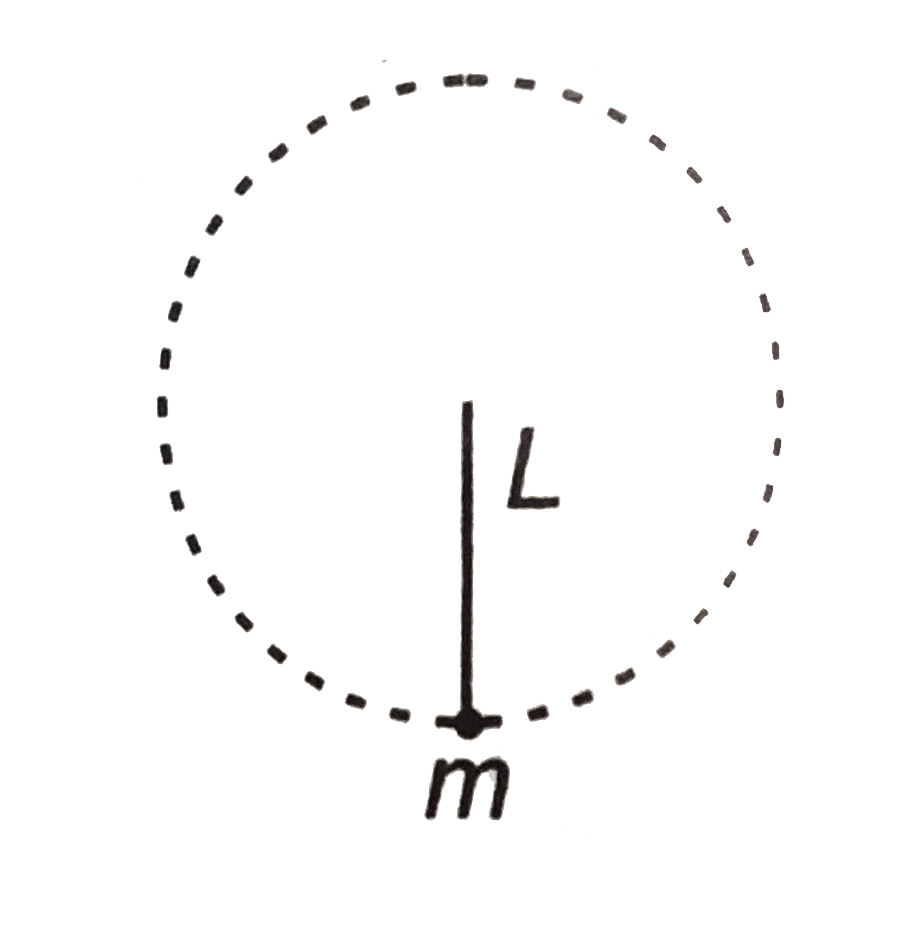 View Solution
View SolutionA small particle of mass m attached with a light inextensible thread of length L is moving in a verical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Minimum velocity of the particle is
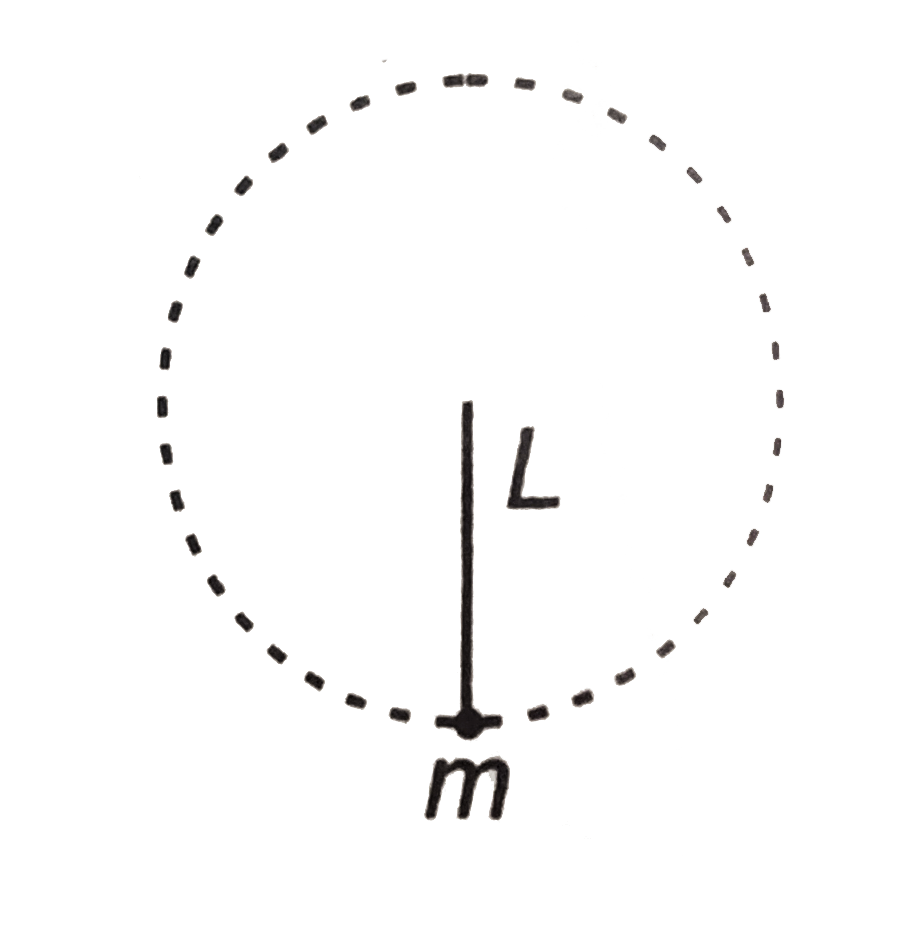 View Solution
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
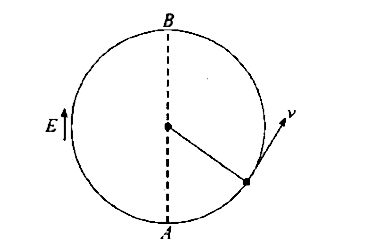 View Solution
View Solution


